 割圜密率捷法卷一
割圜密率捷法卷一
割圜密率捷法,清代數學家明安圖積三十年之功寫成;後子明新、弟子陳際新根據明安圖遺稿整理、推究於乾隆三十九年(1774年)出版,時明安圖已去世十年。[1]
《割圜密率捷法》根據連比例三角形的性質,詳細推導圓周率的九個無窮級數。中算史家李儼說「數與形的結合,堪與笛卡爾所創立的解析幾何媲美」[2]。
卷一 步法
 +…………
+…………
可以改寫成
 [3]。
[3]。
此展開式被清代數學家稱為「杜氏第一術」,出自牛頓。
杜氏九術之二,出自格列高里:[4].
弧背為a,半徑為r,通弦為c
 ……
……
「杜氏九術」之三,出自格列高里
 …………
…………
 +……
+……
 +…………
+…………
出自明安圖:
![{\displaystyle 2a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*c^{2n+1}}{4^{n}*(2n+1)!*r^{2n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e38a9daf7f8d28f118dd35bf4e05f0417989da) [5]。
[5]。
出自明安圖
![{\displaystyle a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*(r*sin\alpha )^{2n+1}}{(2n+1)!*r^{2n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bb749920fa6314f5f53171dc02d9cac8f449c1) [6]。
[6]。
 [7]。
[7]。
 [8]。
[8]。




- 余矢餘弦求本弧
- 借弧背求正弦餘弦
- 借正弦餘弦求弧背
卷二 用法
- 角度求八線
- 直線三角形邊角相求
- 弧線三角形邊角相求
卷三 法解上
 分弧通弦率數求全弧通弦率圖解
分弧通弦率數求全弧通弦率圖解
 明安圖鎮此書中最先運用卡塔蘭數
明安圖鎮此書中最先運用卡塔蘭數
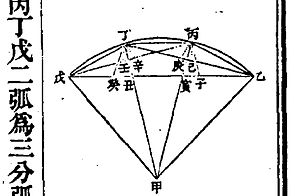 弧背求通弦圖解
弧背求通弦圖解
- 分弧通弦率數求全弧通弦率法解
- 弧背求通弦法解
- 通弦求弧背法解
- 弧背正弦相求法解
卷四 法解下
- 分弧正矢率數求全弧正矢率數法解
- 弧背求正矢法解
- 正矢求弧背法解
- 弧矢相求法解
- 弧矢弦正余互用法解
- 借弧背求正弦餘弦法解
- 借正弦餘弦求弧背法解
- ^ 吳文俊主編 《中國數學史大系》第七卷 447頁
- ^ 李儼 《明清算家的割圓術研究》《李儼錢寶琮科學史全集》第7卷第 297頁
- ^ 羅見今 第20頁
- ^ 羅見今 第22頁
- ^ 羅見今 第28頁
- ^ 羅見今 30頁
- ^ 羅見今 31頁
- ^ 羅見今 33頁
- 明安圖著 《割圜密率捷法》卷一、二、三
- 明安圖原著 羅見今譯註 《割圜密率捷法》釋注 內蒙古教育出版社 1998
- Yoshio Mikami Development of Mathematics in China and Japan, Leipzig, 1912
- Jami C, Etude du Livre "Methods Rapides des Trigonometrie et du Rapport Precis du Cercle" de Ming Antu,1985.











![{\displaystyle 2a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*c^{2n+1}}{4^{n}*(2n+1)!*r^{2n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e38a9daf7f8d28f118dd35bf4e05f0417989da)
![{\displaystyle a=\sum _{n=0}^{\infty }{\frac {[(2n-1)!!]^{2}*(r*sin\alpha )^{2n+1}}{(2n+1)!*r^{2n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bb749920fa6314f5f53171dc02d9cac8f449c1)





