调日法[1]是南北朝数学家何承天发明的一种系统地寻找最佳逼近(帕德近似)以表示天文数据或数学常数的内插法。据宋史卷七十四:“宋世何承天,更以四十九分之二十六为强率,十七分之九为弱率;于强弱之际,以求日法……自后治历者,莫不因承天法,累强弱之数”调日法后來传入日本。
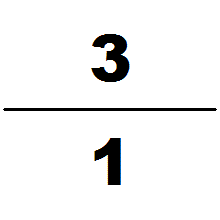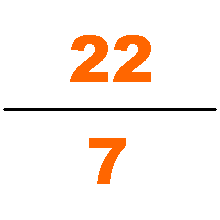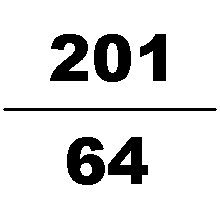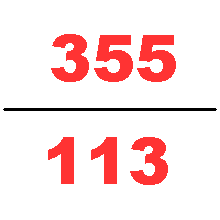
中国有学者认为祖冲之可能利用何承天的调日法求得圆周率的约率和密率:
- 圆周率的约率为

- 圆周率的密率为

何承天的调日法是他对数学的一项重要贡献。一千年以后,15世纪法国数学家尼古拉·休凯(1455年 ━ 1488年),才使用相似的插入法。
何承天调日法原理[编辑]
已知
则
推而广之:
 ,其中 m,k 为正整数。
,其中 m,k 为正整数。
欲求精确分数 使
使 ,其中
,其中 为误差界限。
为误差界限。
令 为弱率,
为弱率, 为强率。
为强率。
第一步,根据下列方法求得一个近似分数

如果 ,则将
,则将 作为新的强分数,和旧弱分数
作为新的强分数,和旧弱分数  调日得到近似分数:
调日得到近似分数:

如果 , 则将
, 则将 作为新的弱分数,和旧强分数
作为新的弱分数,和旧强分数  调日得到近似分数:
调日得到近似分数:

反复操作,到 为止。
为止。
另外,还可以直接求m,k的数值,加快逼近速度:
若 ,且
,且  以及
以及
如果有正整数m,k满足:
那么就有:
证明如下:由条件可得

而根据 又有
又有

代入上面的两个关系式可得:

解关于x的一元一次方程就有结果:

何承天调日法被同时代和后代数学家如赵爽,祖冲之,一行等运用。
朔望月[编辑]
何承天将  作为朔望月零数部分的弱率,以
作为朔望月零数部分的弱率,以 作为朔望月零数部分的强率。运用调日法,最后得到
作为朔望月零数部分的强率。运用调日法,最后得到  ,根据他的观测数值0.530585,首先计算d1,d2
,根据他的观测数值0.530585,首先计算d1,d2

寻找满足以下关系的m,k值:

可以令(m,k)=(1,15)
从而得到:

727年唐朝天文学家一行在《大衍历》中用同样的弱率和强率求得 
闰周问题[编辑]
南北朝数学家祖冲之熟悉调日术,他以 为弱率,
以
为弱率,
以 为强率,通过调日法得到
为强率,通过调日法得到
近点月[编辑]
何承天以 为弱率,以
为弱率,以 为强率,用调日法求得近点月为
为强率,用调日法求得近点月为 。祖冲之也得到高精度的数值
。祖冲之也得到高精度的数值
圆周率约率和密率[编辑]
祖冲之求圆周率约率和密率的方法已失传。有学者认为他用刘徽割圆术求得圆周率的约率和密率 ;也有学者认为祖冲之有可能用何承天的调日法求得圆周率的约率和密率的分数表示式[2]。 祖冲之对调日法是熟悉的,他自己就用过调日法改进何承天近点月 为更加精确的
为更加精确的
取 ,先只考虑小数部分,根据
,先只考虑小数部分,根据 ,用调日法进行计算:
,用调日法进行计算:

寻找满足以下关系的m,k值:

所以可以令(m,k)=(1,15),从而可以得到结果:

祖冲之密率  和π之误差为0.0000002668。下一个[來源請求]比之更為精确的分数为
和π之误差为0.0000002668。下一个[來源請求]比之更為精确的分数为  误差为 -0.0000002662,分子、分母都比祖冲之密率的分子、分母複雜得多。
误差为 -0.0000002662,分子、分母都比祖冲之密率的分子、分母複雜得多。
祖冲之很可能先用刘徽割圆术求出圆周率。刘徽割圆术计算需要多次开平方运算,例如用八次割圆术得到  [3], 无论分子分母都比祖冲之密率的分子分母复杂,但还不如密率的分数表示准确。用十一次割圆术可得到和密率相当精确但比较复杂的分数,再通过调日法求得准确而又简单的分数式。
[3], 无论分子分母都比祖冲之密率的分子分母复杂,但还不如密率的分数表示准确。用十一次割圆术可得到和密率相当精确但比较复杂的分数,再通过调日法求得准确而又简单的分数式。
调日法后传入日本。日本数学家关孝和(Seki, Takakazu, 1642-1708)在《括要算法》一书中称之为零约术,并用之得出圆周率的近似分数为  [4],正是祖冲之的密率。
[4],正是祖冲之的密率。
黄金分割:

用调日法求分数表示:

分母1,2,3,5,8,13,21,....正是斐波那契数列。
- √2=1.4142135623 ~=

- √3=1.7320508075 ~=

- √5=2.2360679775 ~=

- √10=3.162277660 ~=

![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35) =1.059463094~=
=1.059463094~=
- e=2.718281828 ~=

- 普朗克常数 ~=
 x10-34
x10-34
- 万有引力常数 G~=
 x10-11
x10-11
- 阿伏伽德罗常量~=
 x1023
x1023
- 玻尔兹曼常数~=
 x10-23
x10-23
参考文献[编辑]
- ^ 中國古时将天文数据的小数部分的分母称为「日」,「调日术」即是调节分母的意思。
- ^ 吴文俊 主编 《中国数学史大系》第四卷 123页,ISBN7-300-0425-8/O
- ^ 傅海伦编著 《中外数学史概论》 第四章 刘徽的割圆术 51页 科学出版社,ISBN978-7-03-018477-1
- ^
吴文俊 主编 《中国数学史大系》第四卷 125页,ISBN7-300-0425-8/O























































![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)





