跳转到内容

ROC曲线

本页使用了标题或全文手工转换
维基百科，自由的百科全书
3条ROC曲线

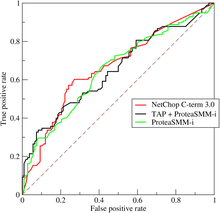
在信号检测理论中，接收者操作特征曲线，或者叫ROC曲线（英语：Receiver operating characteristic curve），是一种坐标图式的分析工具，用于选择最佳的信号侦测模型、舍弃次佳的模型或者在同一模型中设置最佳阈值。

在做决策时，ROC分析能不受成本／效益的影响，给出客观中立的建议。

ROC曲线首先是由二战中的电子工程师和雷达工程师发明的，用来侦测战场上的敌军载具（飞机、船舰），也就是信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。数十年来，ROC分析被用于医学、无线电、生物学、犯罪心理学领域中，而且最近在机器学习（machine learning）和数据挖掘（data mining）领域也得到了很好的发展。

基本概念

[编辑]
术语
阳性 (P, positive)
阴性 (N, Negative)
真阳性 (TP, true positive)
正确的肯定。又称：命中 (hit)
真阴性 (TN, true negative)
正确的否定。又称：正确拒绝 (correct rejection)
伪阳性 (FP, false positive)
错误的肯定，又称：假警报 (false alarm)，第一型错误
伪阴性 (FN, false negative)
错误的否定，又称：未命中 (miss)，第二型错误
真阳性率 (TPR, true positive rate)
又称：命中率 (hit rate)、敏感度(sensitivity)
TPR = TP / P = TP / (TP+FN)
伪阳性率(FPR, false positive rate)
又称：错误命中率，假警报率 (false alarm rate)
FPR = FP / N = FP / (FP + TN)
准确度 (ACC, accuracy)
ACC = (TP + TN) / (P + N)
即：(真阳性+真阴性) / 总样本数
真阴性率 (TNR)
又称：特异度 (SPC, specificity)
SPC = TN / N = TN / (FP + TN) = 1 - FPR
阳性预测值 (PPV)
PPV = TP / (TP + FP)
阴性预测值 (NPV)
NPV = TN / (TN + FN)
假发现率 (FDR)
FDR = FP / (FP + TP)
Matthews相关系数 (MCC)，即 Phi相关系数
F1评分
F1 = 2TP/(P+P')
Source: Fawcett (2006).
参见：第一型及第二类错误和灵敏度和特异度

分类模型（又称分类器，或诊断）是将一个实例映射到一个特定类的过程。ROC分析的是二元分类模型，也就是输出结果只有两种类别的模型，例如：（阳性／阴性）（有病／没病）（垃圾邮件／非垃圾邮件）（敌军／非敌军）。

当信号侦测（或变量测量）的结果是一个连续值时，类与类的边界必须用一个阈值（英语：threshold）来界定。举例来说，用血压值来检测一个人是否有高血压，测出的血压值是连续的实数（从0~200都有可能），以收缩压140／舒张压90为阈值，阈值以上便诊断为有高血压，阈值未满者诊断为无高血压。二元分类模型的个案预测有四种结局：

  1. 真阳性（TP）：诊断为有，实际上也有高血压。
  2. 伪阳性（FP）：诊断为有，实际却没有高血压。
  3. 真阴性（TN）：诊断为没有，实际上也没有高血压。
  4. 伪阴性（FN）：诊断为没有，实际却有高血压。

这四种结局可以画成2 × 2的混淆矩阵：

  真实值 总
数
p n
预
测
输
出 		p' 真阳性
(TP)		 伪阳性
(FP)		 P'
n' 伪阴性
(FN)		 真阴性
(TN)		 N'
总数 P N

ROC空间

[编辑]

ROC空间将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴。

  • TPR：在所有实际为阳性的样本中，被正确地判断为阳性之比率。
  • FPR：在所有实际为阴性的样本中，被错误地判断为阳性之比率。

给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。 在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。

完美的预测是一个在左上角的点，在ROC空间座标 (0,1)点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。

让我们来看在实际有100个阳性和100个阴性的案例时，四种预测方法（可能是四种分类器，或是同一分类器的四种阈值设置）的结果差异：

A B C C'
TP=63 FP=28 91
FN=37 TN=72 109
100 100 200
TP=77 FP=77 154
FN=23 TN=23 46
100 100 200
TP=24 FP=88 112
FN=76 TN=12 88
100 100 200
TP=76 FP=12 88
FN=24 TN=88 112
100 100 200
TPR = 0.63 TPR = 0.77 TPR = 0.24 TPR = 0.76
FPR = 0.28 FPR = 0.77 FPR = 0.88 FPR = 0.12
ACC = 0.675 ACC = 0.500 ACC = 0.180 ACC = 0.820
ROC空间的4个例子

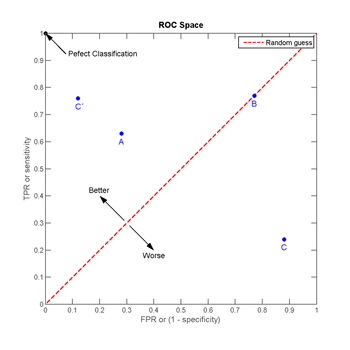
将这4种结果画在ROC空间里：

  • 点与随机猜测线的距离，是预测力的指针：离左上角越近的点预测（诊断）准确率越高。离右下角越近的点，预测越不准。
  • 在A、B、C三者当中，最好的结果是A方法。
  • B方法的结果位于随机猜测线（对角线）上，在例子中我们可以看到B的准确度（ACC，定义见前面表格）是50%。
  • C虽然预测准确度最差，甚至劣于随机分类，也就是低于0.5（低于对角线）。然而，当将C以 (0.5, 0.5) 为中点作一个镜像后，C'的结果甚至要比A还要好。这个作镜像的方法，简单说，不管C（或任何ROC点低于对角线的情况）预测了什么，就做相反的结论。

ROC曲线

[编辑]
随着阈值调整，ROC座标系里的点如何移动

上述ROC空间里的单点，是给定分类模型且给定阈值后得出的。但同一个二元分类模型的阈值可能设置为高或低，每种阈值的设置会得出不同的FPR和TPR。

  • 将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里，就成为特定模型的ROC曲线。

例如右图，人体的血液蛋白浓度是呈正态分布的连续变量，病人的分布是红色，平均值为A g/dL，健康人的分布是蓝色，平均值是C g/dL。健康检查会测量血液样本中的某种蛋白质浓度，达到某个值（阈值，threshold）以上诊断为有疾病征兆。研究者可以调整阈值的高低（将左上图的B垂直线往左或右移动），便会得出不同的伪阳性率与真阳性率，总之即得出不同的预测准确率。

1. 由于每个不同的分类器（诊断工具、侦测工具）有各自的测量标准和测量值的单位（标示为：“健康人－病人分布图”的横轴），所以不同分类器的“健康人－病人分布图”都长得不一样。

2. 比较不同分类器时，ROC曲线的实际形状，便视两个实际分布的重叠范围而定，没有规律可循。

3. 但在同一个分类器之内，阈值的不同设置对ROC曲线的影响，仍有一些规律可循：

  • 当阈值设置为最高时，亦即所有样本都被预测为阴性，没有样本被预测为阳性，此时在伪阳性率 FPR = FP / ( FP + TN ) 算式中的 FP = 0，所以 FPR = 0%。同时在真阳性率（TPR）算式中， TPR = TP / ( TP + FN ) 算式中的 TP = 0，所以 TPR = 0%
→ 当阈值设置为最高时，必得出ROC座标系左下角的点 (0, 0)。
  • 当阈值设置为最低时，亦即所有样本都被预测为阳性，没有样本被预测为阴性，此时在伪阳性率FPR = FP / ( FP + TN ) 算式中的 TN = 0，所以 FPR = 100%。同时在真阳性率 TPR = TP / ( TP + FN ) 算式中的 FN = 0，所以 TPR=100%
→ 当阈值设置为最低时，必得出ROC座标系右上角的点 (1, 1)。
  • 因为TP、FP、TN、FN都是累积次数，TN和FN随着阈值调低而减少（或持平），TP和FP随着阈值调低而增加（或持平），所以FPR和TPR皆必随着阈值调低而增加（或持平）。
→ 随着阈值调低，ROC点 往右上（或右／或上）移动，或不动；但绝不会往左下(或左／或下)移动。

曲线下面积（AUC）

[编辑]
例示三种AUC值（曲线下面积）

在比较不同的分类模型时，可以将每个模型的ROC曲线都画出来，比较曲线下面积做为模型优劣的指针。

意义

[编辑]

ROC曲线下方的面积（英语：Area under the Curve of ROC (AUC ROC)），其意义是：

  • 因为是在1x1的方格里求面积，AUC必在0~1之间。
  • 假设阈值以上是阳性，以下是阴性；
  • 若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之概率 [1]。
  • 简单说：AUC值越大的分类器，正确率越高。

从AUC判断分类器（预测模型）优劣的标准：

  • AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
  • 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设置阈值的话，能有预测价值。
  • AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
  • AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

计算

[编辑]

AUC的计算有两种方式，都是以逼近法求近似值。

梯形法

[编辑]

梯形法（英语：trapezoid method）：简单地将每个相邻的点以直线连接，计算连线下方的总面积。因为每一线段下方都是一个梯形，所以叫梯形法。

  • 优点：简单，所以常用。
  • 缺点：倾向于低估AUC。

ROC AUCH法

[编辑]

潜在问题

[编辑]

AUC of ROC是机器学习的社群最常使用来比较不同模型优劣的方法[2] 。然而近来这个做法开始受到质疑，因为有些机器学习的研究指出，AUC的杂讯太多，并且很常求不出可信又有效的AUC值（此时便不能保证AUC传达本节开头所述之意义），使得AUC在模型比较时产生的问题比解释的问题更多[3][4][5] 。

分析软件

[编辑]

所有常用于统计分析的软件（例：SPSS、SAS、SYSTAT、S-Plus、ROCKIT、RscorePlus）都有依据不同阈值自动计算真阳性和伪阳性比率、并依此绘制ROC曲线的功能。

离散分类器（英语：discrete，或称“间断分类器”），如决策树，产生的是离散的数值或者一个二元标签。应用到实例中，这样的分类器最后只会在ROC空间产生单一的点。而一些其他的分类器，如朴素贝叶斯分类器，逻辑斯谛回归或者人工神经网络，产生的是实例属于某一类的可能性，对于这些方法，一个阈值就决定了ROC空间中点的位置。举例来说，如果可能值低于或者等于0.8这个阈值就将其认为是阳性的类，而其他的值被认为是阴性类。这样就可以通过画每一个阈值的ROC点来生成一个生成一条曲线。MedCalc是较好的ROC曲线分析软件。

参考文献

[编辑]

引用

[编辑]
  1. ^ Fawcett, Tom (2006); An introduction to ROC analysis, Pattern Recognition Letters, 27, 861–874.
  2. ^ Hanley, James A.; McNeil, Barbara J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology. 1983-09-01, 148 (3): 839–843 [2008-12-03]. PMID 6878708. （原始内容存档于2008-09-05）. 
  3. ^ Hanczar, Blaise; Hua, Jianping; Sima, Chao; Weinstein, John; Bittner, Michael; and Dougherty, Edward R. (2010); Small-sample precision of ROC-related estimates, Bioinformatics 26 (6): 822–830
  4. ^ Lobo, Jorge M.; Jiménez-Valverde, Alberto; and Real, Raimundo (2008), AUC: a misleading measure of the performance of predictive distribution models, Global Ecology and Biogeography, 17: 145–151
  5. ^ Hand, David J. (2009); Measuring classifier performance: A coherent alternative to the area under the ROC curve, Machine Learning, 77: 103–123

来源

[编辑]
  • Zou, K.H., O'Malley, A.J., Mauri, L. (2007). Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models. Circulation, 6;115(5):654–7.
  • X. H., Zhou. Statistical Methods in Diagnostic Medicine. Wiley & Sons. 2002. ISBN 9780471347729. 
  • Lasko, T.A., J.G. Bhagwat, K.H. Zou and Ohno-Machado, L. (2005). The use of receiver operating characteristic curves in biomedical informatics. Journal of Biomedical Informatics, 38(5):404–415.
  • Balakrishnan, N., (1991) Handbook of the Logistic Distribution, Marcel Dekker, Inc., ISBN 978-0824785871.
  • Gonen M., (2007) Analyzing Receiver Operating Characteristic Curves Using SAS, SAS Press, ISBN 978-1-59994-298-1.
  • Green, W.H., (2003) Econometric Analysis, fifth edition, Prentice Hall, ISBN 0-13-066189-9.
  • Heagerty, P.J., Lumley, T., Pepe, M. S. (2000) Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker Biometrics, 56:337–344
  • Hosmer, D.W. and Lemeshow, S., (2000) Applied Logistic Regression, 2nd ed., New York; Chichester, Wiley, ISBN 0-471-35632-8.
  • Brown, C.D., and Davis, H.T. (2006) Receiver operating characteristic curves and related decision measures: a tutorial, Chemometrics and Intelligent Laboratory Systems, 80:24–38
  • Mason, S.J. and Graham, N.E. (2002) Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q.J.R. Meteorol. Soc., 128:2145–2166.
  • Pepe, M.S. (2003). The statistical evaluation of medical tests for classification and prediction. Oxford. ISBN 0198565828.
  • Carsten, S. Wesseling, S., Schink, T., and Jung, K. (2003) Comparison of Eight Computer Programs for Receiver-Operating Characteristic Analysis. Clinical Chemistry, 49:433–439
  • Swets, J.A. (1995). Signal detection theory and ROC analysis in psychology and diagnostics: Collected papers. Lawrence Erlbaum Associates.
  • Swets, J.A., Dawes, R., and Monahan, J. (2000) Better Decisions through Science. Scientific American, October, pages 82–87.

外部链接

[编辑]
检索自“https://zh.wikipedia.org/w/index.php?title=ROC曲线&oldid=79406601”