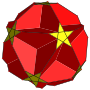
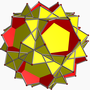
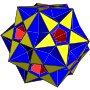
大星形截角十二面体

大星形截角十二面体

类别	星形均匀多面体
对偶多面体	大三角化二十面体
识别
名称	大星形截角十二面体
参考索引	U66, C83, W104
鲍尔斯缩写	quit gissid
数学表示法
威佐夫符号	2 3 | 5/3
性质
面	32
边	90
顶点	60
欧拉特征数	F=32, E=90, V=60 （χ=2）
组成与布局
顶点图	10/3.10/3.3
顶点布局	20{3}+12{10/3}
对称性
对称群	Ih, [5,3], *532
图像
10/3.10/3.3 （顶点图） 大三角化二十面体 （对偶多面体）

在几何学中，大星形截角十二面体又称为星形截角大十二面体是一种由十角星和三角形组成星形多面体，索引为U₆₆，对偶多面体是大三角化二十面体。

性质

大星形截角十二面体共有32个面、90条边和60个顶点，在其32个面中，有20个正三角形和12个十角星，且每个顶点都是2个十角星和1个三角形的公共顶点，顶点图可以用¹⁰/₃.¹⁰/₃.3表示。在施莱夫利符号中计为t_0,1{⁵/₃,3}、考克斯特记号中可以用表示。

其可以视为在正二十面体每个面的角落放上三角锥，类似于将正二十面体进行星形截角变换，但又与实际上真的进行星形截角变换的正二十面体不太相同。

顶点座标

边长为1单位且几何中心位于原点的大星形截角十二面体，其顶点座标为：

(0, ±τ, ±(2−1/τ))、

(±τ, ±1/τ, ±2/τ)、

(±1/τ², ±1/τ, ±2)

其中，τ为黄金比例，其值为${\frac {1+{\sqrt {5}}}{2}}\approx 1.68$，有时会以符号φ表示。

二面角

大星形截角十二面体有2种二面角，分别为十角星-十角星二面角以及十角星-三角形二面角。十角星-十角星二面角的角度为为五平方根倒数的反余弦值：

$\cos ^{-1}({\frac {\sqrt {5}}{5}})\approx 1.1071\approx 63.4349^{\circ }$

而十角星-三角形二面角的角度为：

$\cos ^{-1}({\frac {\sqrt {15(5-2{\sqrt {5}})}}{15}})\approx 1.382\approx 79.18768^{\circ }$

使用

有一种魔术方块使用大星形截角十二面体作为其外型。

相关多面体

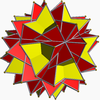大星形截角十二面体

小二十面化截半二十面体

小二重三角十二面截半二十面体

小十二面二十面体

对偶复合体

星形截角立方体与其对偶的复合体为复合大星形截角十二面体大三角化二十面体。其共有92个面、180条边和92个顶点，其欧拉示性数为4，亏格为-1，有12个非凸面。

参见

• 星形截角
• 正十二面体

外部链接

• 埃里克·韦斯坦因. 大星形截角十二面体. MathWorld.