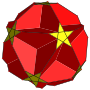
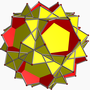
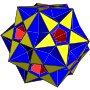
扭棱小星形十二面体

扭棱小星形十二面体

类别	均匀星形多面体
对偶多面体	中五角六十面体
识别
名称	扭棱小星形十二面体 Snub dodecadodecahedron
参考索引	U40, C49, W111
鲍尔斯缩写	siddid
数学表示法
考克斯特符号
施莱夫利符号	sr{5⁄2,5}
威佐夫符号	| 2 5⁄2 5
性质
面	84
边	150
顶点	60
欧拉特征数	F=84, E=150, V=60 （χ=-6）
组成与布局
面的种类	20个正三角形 12个正五边形 12个正五角星
顶点图	3.3.5⁄2.3.5
对称性
对称群	Ih, [5,3]+, 532
图像
3.3.5⁄2.3.5 （顶点图） 中五角六十面体 （对偶多面体）

在几何学中，扭棱小星形十二面体是一种星形均匀多面体，索引为U₄₀，由60个三角形面、12个正五边形面和12个正五角星面组成，且有12组正五边形面和正五角星面互相平行，为小星形十二面体经扭棱变换后的结果，具有二十面体群对称性。 扭棱小星形十二面体的对偶多面体为中五角六十面体，并与反扭棱小星形十二面体拓朴同构。

性质

扭棱小星形十二面体一共有84个面、150条边和60个顶点。在其84个面中，有60个正三角形面、12个正五边形面和12个五角星面，换句话说，具有3条边的面共60个且具有5条边的面共24个。其12个正五边形面和12个五角星面中，有12组正五边形面和五角星面互相平行，这与截半大十二面体非常类似。其60个顶点每个顶点都是1个十角星、1个五角星和3个三角形的公共顶点，并且这些面在顶都周围皆是依照五角星、三角形、五边形、三角形、三角形和三角形的顺序排列，在顶点图中可以用(5⁄2,3,5,3,3)或(3.3.5⁄2.3.5)来表示。

表示法

扭棱小星形十二面体在考克斯特—迪肯符号中可以表示为（s5⁄2s5s），在施莱夫利符号中可以表示为sr{5⁄2,5}，在威佐夫记号中可以表示为| 2 5⁄2 5。

尺寸

若扭棱小星形十二面体的边常为单位长，则其外接球半径为多项式$64x^{4}-192x^{3}+180x^{2}-65x+8$之较大正实根（约为1.6242）的平方根，约为1.27443994：

${\sqrt {\operatorname {root} \left(64x^{4}-192x^{3}+180x^{2}-65x+8\right)}}\approx 1.27443988203802179$

中分球半径则为多项式$256x^{4}-512x^{3}+240x^{2}-28x+1$之正实根的平方根：

${\sqrt {\operatorname {root} \left(256x^{4}-512x^{3}+240x^{2}-28x+1\right)}}\approx 1.172261495114928$

顶点座标

扭棱小星形十二面体的顶点座标为下列座标的偶置换：

(±2α, ±2, ±2β),

(±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1))、

(±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ))、

(±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) 与

(±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1))，

带有偶数个正号，其中

β = (α²/τ+τ)/(ατ−1/τ)，

当中的 τ = (1+√5)/2为黄金比例且 α是多项式τα⁴−α³+2α²−α−1/τ的正实根，约为0.7964421。 若上述座标使用奇置换并带有奇数个正号的话，则会得到扭棱小星形十二面体的另一种形式，即另一种形式的对映体。

参见

• 均匀多面体列表
• 反扭棱小星形十二面体