双丸塔
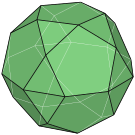  以同相(左)/异相(右)双五角丸塔为例 | ||
| 类别 | 双丸塔 | |
|---|---|---|
| 对偶多面体 | 见#对偶多面体一节 | |
| 性质 | ||
| 面 | ||
| 边 | ||
| 顶点 | ||
| 欧拉特征数 | F=, E=, V= (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 2个n边形 2n个五边形 4n个三角形 | |
| 对称性 | ||
| 对称群 | 同相:Dnh, [n,2], (*n22), 4n阶 异相:Dnd, [2n,2+], (2*n), 4n阶 | |
| 旋转对称群 | Dn, [n,2]+, (n22), 2n阶 | |
| 特性 | ||
| 凸 | ||
| 图像 | ||
| ||
| 注:为底面边数 。 | ||
在几何学中,双罩帐又称为双丸塔(birotunda),是指一系列属于二面体群的多面体,由两个丸塔通过边数较大的底面以底面对底面的方式贴合而成[1]。 其与双台塔类似但不是正方形和三角形交替构成,而是五边形和三角形交替并绕轴构成。双丸塔有两种形式,分别为以相同相位叠合,称为同相双丸塔(orthobirotunda)[2], 和以相异相位叠合,称为异相双丸塔(gyrobirotunda)[2]。 同相双丸塔可以视为丸塔以边数较多的底面作为镜像面镜射产生另一个丸塔组合而成的立体;而异相双丸塔则为两个丸塔之间除了是镜像之外,还差了一个旋转角叠合构成。
双五角丸塔是唯一一个能够以所有面皆为正多边形的形式存在的丸塔。 两种形式中,一个是约翰逊多面体,另一个是半正多面体:[3]
例子[编辑]
双丸塔有无限多种,最小的双丸塔是双三角丸塔。能以所有面皆为正多边形之形式存在的双丸塔只有双五角丸塔[2],其他双丸塔的五边形面都会有一定程度的形变,即使其所有边等长,也未必能所有角等角。[2]
双丸塔根据两底面的方向性可以分成“同相”和“异相”两种情况。其中,“同相”表示顶面和底面相同方向,而“异相”则表示顶面和底面差了一个旋转角,角度为底面多边形中心角的一半。
| 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|
 同相双四角丸塔 |
 同相双五角丸塔 |
 同相双六角丸塔 |
 同相双七角丸塔 |
 同相双八角丸塔 |
 异相双四角丸塔 |
 异相双五角丸塔 |
 异相双六角丸塔 |
 异相双七角丸塔 |
 异相双八角丸塔 |
对偶多面体[编辑]
  以同相/异相双六角丸塔的对偶多面体为例 | |
| 类别 | 双丸塔对偶 |
|---|---|
| 性质 | |
| 面 | |
| 边 | |
| 顶点 | |
| 欧拉特征数 | F=, E=, V= (χ=2) |
| 组成与布局 | |
| 面的种类 | 同相:
异相: |
| 对称性 | |
| 对称群 | 同相:Dnh, [n,2], (*n22), 4n阶 异相:Dnd, [2n,2+], (2*n), 4n阶 |
| 旋转对称群 | Dn, [n,2]+, (n22), 2n阶 |
| 特性 | |
| 凸 | |
| 注:为底面边数 。 | |
双丸塔可以分成同相双丸塔和异相双丸塔,这两种立体的对偶多面体各不相同。其中,异相双丸塔的对偶多面体由筝形或菱形组成,尤其是异相双五角丸塔的对偶多面体全部皆由菱形构成,是一种卡塔兰立体——菱形三十面体[5]。
| 4 | 5 | 6 | 7 |
|---|---|---|---|
 异相双四角丸塔 的对偶多面体 |
 异相双五角丸塔 的对偶多面体 菱形三十面体 |
 异相双六角丸塔 的对偶多面体 |
 异相双七角丸塔 的对偶多面体 |
 异相双四角丸塔 |
 异相双五角丸塔 |
 异相双六角丸塔 |
 异相双七角丸塔 |
而同相双丸塔的对偶多面体除了构成异相双丸塔的筝形和菱形外,还会在赤道面上有一圈梯形。
| 4 | 5 | 6 | 7 |
|---|---|---|---|
 同相双四角丸塔 的对偶多面体 |
 同相双五角丸塔 的对偶多面体 |
 同相双六角丸塔 的对偶多面体 |
 同相双七角丸塔 的对偶多面体 |
 同相双四角丸塔 |
 同相双五角丸塔 |
 同相双六角丸塔 |
 同相双七角丸塔 |
相关多面体[编辑]
双丸塔柱[编辑]
双丸塔柱是指在双丸塔的两个丸塔中间加入柱体所形成的立体,与双丸塔一样,可分为“同相”及“异相”两种。仅有同相五角双丸塔柱和异相五角双丸塔柱属于约翰逊多面体。[6][7]
| 4 | 5 | 6 | 7 |
|---|---|---|---|
 同相双四角丸塔柱 |
 同相五角双丸塔柱 |
 同相双六角丸塔柱 |
 同相双七角丸塔柱 |
 异相双四角丸塔柱 |
 异相五角双丸塔柱 |
 异相双六角丸塔柱 |
 异相双七角丸塔柱 |
双丸塔反角柱[编辑]
双丸塔反角柱又称为双丸塔反棱柱是指在双丸塔的两个丸塔中间加入反角柱所形成的立体。仅有双五角丸塔反角柱属于约翰逊多面体。[8]
| 4 | 5 | 6 | 7 |
|---|---|---|---|
 双四角丸塔反角柱 |
 双五角丸塔反角柱 |
 双六角丸塔反角柱 |
 双七角丸塔反角柱 |
参考文献[编辑]
- ^ Weisstein, Eric W. (编). Birotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 2.0 2.1 2.2 2.3 Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- ^ Victor A. Zalgaller. Convex Polyhedra with Regular Faces. Consultants Bureau. 1969. No ISBN.
- ^ Icosidodecahedron. polyhedra.tessera.li. [2023-01-17]. (原始内容存档于2023-01-17).
- ^ Icosidodecahedron. polyhedrongarden.com. [2023-01-17]. (原始内容存档于2023-01-17).
- ^ Weisstein, Eric W. (编). Elongated Pentagonal Orthobirotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Elongated Pentagonal Gyrobirotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Gyroelongated Pentagonal Birotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
| |||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||





