跳转到内容

天文学大成

维基百科，自由的百科全书
天文学大成的拉丁文版本图片

《天文学大成》（拉丁语：Almagestum），又译《至大论》，古希腊托勒密在约公元140年编纂的一部数学、天文学专著，提出了恒星和行星的复杂运动路径。直到中世纪和文艺复兴早期，该书提出的地心说模型被伊斯兰和欧洲社会接受长达一千多年。天文学大成是古希腊天文学最重要的信息来源。该书对数学学者也很有价值，因为它记载了古希腊数学家喜帕恰斯已经遗失的著作。喜帕恰斯论述了三角法，但是该著作已经丢失，数学家大体上使用托勒密的书籍来当做喜帕恰斯著作和古希腊三角法的资料。

该书的古希腊语原名《数学论》（Μαθηματικἠ Σύνταξις，Mathematikē Sýntaxis），９世纪阿拉伯语译成《المجسطي》(al-majisṭī，字面意思为“最宏大的”，即现代中文译名《天文学大成》的来由），因为古希腊语原文一度在西欧散佚，1175年的拉丁语译本译自阿拉伯语，采用了阿拉伯语的译名，这译名自此在全欧通行。

成书的日期

[编辑]

对《天文学大成》完成的日期近来做了更经确的估计，托勒密在147或148年于埃及亚力山大城东方约25公里的Canopus(在现在的尼罗河三角洲)设立了公开的碑文。稍后，N.T.汉弥敦发现Canopic碑文所载的托勒密模型的版本早于《天文学大成》的版本，因此《天文学大成》完成的时间不会早于托勒密开始观察工作之后的四分之一世纪的150年[1]。

书籍内容

[编辑]

书籍

[编辑]
以地球为中心的太阳和行星视运动。

在1515年印制的这一版《天文学大成》包含13卷（称为book），总共有152页[2]。

  • 卷一，是对亚里士多德宇宙论的概述论的概述：在天球中，地球在中心静止不动，恒星和各个行星绕着地球运转。然后用一组全弦表解释全弦；观察到的黄道（太阳在恒星间的视运动路径）倾角和介绍球面三角学。
  • 卷二包括和归纳天球周日运动相关的问题，换言之就是天体的出没、日夜长短的变化、纬度的测定、垂直在太阳之下的点(日下点)、晷针在分点和至点的影子、和其他因观测者位置造成观测尚的改变。这一卷也利用垂直的平壁研究黄道的角度。
  • 卷三包括一年的长度和太阳的运动。托勒密解释伊巴古发现的分点岁差，和开始解释周转圆的理论。
  • 卷四和卷五涵盖月球的运动、月球视差、月球远地点的运动、月球和太阳相对于地球的大小和距离。
  • 卷六包括太阳和月球的食。
  • 卷七和卷八涵盖恒星的运动，包括分点的进动(岁差)。其中也包含有1022颗恒星的星表，描述它们的位置和所属星座，最亮的那些恒星的视星等被标示为一等星(m=1)，肉眼可见最暗的恒星被标视为六等星(m=6)。每一个星等的亮度是下一个星等的两倍，这是一种对数标尺。这个系统被认为是源自喜帕恰斯，尽管托勒密主张恒星位置是他测定的，但一般也认为是出自喜帕恰斯。
  • 卷九引导出对五颗肉眼可见行星的一般观点和创建的模型，以及水星的运动。
  • 卷十涵盖了金星和火星的运动。
  • 卷十一涵盖了木星和土星的运动。
  • 卷十二涵盖了留和逆行，这些现象发生时行星似乎出现短暂的停止不动，然后有一小段时间在黄道的背景上改变了运动方向。托勒密了解这些现象不仅适用于水星和金星，以适用于外行星。
  • 卷十三涵盖了纬度上的运动，也就是说行星会偏离黄道。

托勒密的宇宙

[编辑]

天文学大成的宇宙论包含五个重点，它们都是该书第一卷的主题。以下是Toomer的翻译过的托勒密的原话：[来源请求]

  • 天体领域是球壳，并且作为天球运动。
  • 地球是球形的。
  • 地球位于宇宙中心。
  • 若提及地球与恒星的距离，地球的体积便可以忽略并当做一个数学上的点来对待。[1]
  • 地球是固定的。

托勒密的行星模型

[编辑]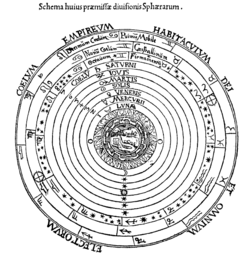
16世纪绘制的托勒密地心说模型。

托勒密把行星球按照下面的顺序安放，从最里面开始依次是：

  1. 月球
  2. 水星
  3. 金星
  4. 太阳
  5. 火星
  6. 木星
  7. 土星
  8. 恒星球

其他古代的作家也曾建议不同的顺序。柏拉图 (c. 427 – c. 347 BC)将太阳放在月球之后做为第二颗；马尔提亚努斯·卡佩拉(公元5世纪)让水星和金星绕着太阳运转；但大多数中世纪伊斯兰和中世纪晚期的欧洲天文学家都以托勒密的学说作为首选。

托勒密继承了希腊前辈的几何学工具和一部分用来预测行星在天空中出现位置的模型。珀加的阿波罗尼奥斯 (c. 262 – c. 190 BC)曾经将均轮和本轮与偏心均轮引入天文学中。喜帕恰斯(公元前2世纪)曾经以精心编制的数学模型解释太阳和月球的运动。喜帕恰斯的一些天文知识传承自美索不达米亚，并且他认为希腊的模型应该比巴比伦的精确，但他未能为依然存在的5颗行星创建经确的模型。

《天文学大成》继承了依巴古以简单的偏心均轮构成的太阳模型。对于月球，托勒密采用了在均轮上的本轮，然后添加了被天文学史家称为"曲柄机构"的装置[3]：他加入了第三个称为偏心均速圆[4]的装置，成功创建了其他行星的模型，而喜帕恰斯曾经失败过。

影响

[编辑]

托勒密写的《天文学大成》被当成数理天文学的教科书。他以圆的结合做基础解释行星的几何模型，组合出行星的几何模型。在稍后的书中，《行星假说》，托勒密解释如何将他的几何模型转换成三维的天球或部分的球。相对于数学的《天文学大成》，《行星假说》有时被称为描述宇宙论的一本书。

托勒密在数里天文学上广泛的论文取代了绝大多数希腊天文学的古老教本。一些更为专业和不会引人入胜的内容，只是单纯的成为过时的新模型。结果是，古老的教本不再被复制，而逐渐失传了。我们知道的许多天文学家的工作，像是喜帕恰斯的，都在《天文学大成》中被引用。

托勒密的《天文学大成》在好几个世纪都是学术上的权威著作。

在9世纪，由两位独力的工作者，主要是哈里发马蒙，首度将之翻译成阿拉伯文。而在当时，《天文学大成》在西欧已经失传了，或是只隐约的流传在占星学的知识中。因此西欧是翻译了阿拉伯文的版本，重新再发现了托勒密。在12世纪，西班牙文的版本产生了，后来又在腓特烈二世 (神圣罗马帝国)的赞助下，从这个版本翻译成拉丁文；克雷莫纳的杰拉德则直接将《天文学大成》从阿拉伯文版翻译成拉丁文。杰拉德在西班牙的托雷多发现阿拉伯文的版本，但是有许多的专有名词是杰拉德不会翻译的，他甚至至将阿拉伯语的喜帕恰斯都保留为阿拉伯文。

在15世纪，西欧出现了希腊文的版本。德国天文学家约翰·缪勒（拉丁名为雷吉奥蒙塔努斯）在希腊教士约翰贝萨里翁授意下制作了拉丁文的精简版。大约在同一时间，特拉布宗的乔治也不仅将原本的文稿，连同评注全都翻译完成。乔治的翻译是在教皇尼古拉斯五世的赞助下进行的，目的是在取代旧有的翻译。新的翻译有很大的改进，但新的评论不仅没有，反倒引起更多的批判[来源请求]。教皇贬低了乔治牺牲奉献的工作[来源请求]，使得雷吉奥蒙塔努斯的译本占了百余年的优势。

Trebizond George: 特拉布宗的乔治翻译的《天文学大成评注》卷十中的一页。在左边， 是水星的模型，显示他在最靠近地球时；在右边，是关于水星的资料，和他对金星这颗行星所做评论的开端。

写过《天文学大成》评论的有亚力山大的塞翁(现存)、亚力山大的帕普斯(仅有残稿留存)、和阿摩纽斯·厄耳墨萨 (失传)。

现代版本

[编辑]

现代通行的校勘本是：

  • Johan Ludvig Heiberg：Claudii Ptolemaei opera quae exstant omnia，莱比锡Teubner出版社：
    • 1. Syntaxis Mathematics. 1898。
    • 2. Opera astronomica minora. 1903。

《天文学大成》有三种英文的翻译版本：第一种是美国马里兰州安纳波利斯圣约翰学院的R. Catesby Taliaferro翻译的，被收录在《西方世界伟大著作》的第16卷。G. J. Toomer稍后也翻译了托勒密的《天文学大成》，于1984年由施普林格出版(ISBN 0-387-91220-7);于1998年由普林斯顿大学出版(ISBN 0-691-00260-6)[来源请求]。最新的版本是Bruce M. Perry翻译的，他也是圣约翰学院的教授[来源请求]。

有一个古老的法文翻译本 (由希腊文直接翻译)，共有二卷，是Nicholas Halma在1813年和1816年分别发表了的，现在可以透过网络在线上阅览：
http://gallica.bnf.fr/ （页面存档备份，存于互联网档案馆）

脚注

[编辑]
  1. ^ 1.0 1.1 Ptolemy. Almagest. 1952. , Book I, Chapter 5.
  2. ^ 存档副本. [2010-03-30]. （原始内容存档于2013-08-28）. 
  3. ^ Michael Hoskin. The Cambridge Concise History of Astronomy.  Chapter 2, page 44.
  4. ^ http://blog.sina.com.cn/s/blog_51fdc06201009m8w.html （页面存档备份，存于互联网档案馆） Equant译名刍议

参见

[编辑]

参考资料

[编辑]
  • James Evans, The History and Practice of Ancient Astronomy, Oxford University Press, 1998 (ISBN 0-19-509539-1)
  • Michael Hoskin, The Cambridge Concise History of Astronomy, Cambridge University Press, 1999 (ISBN 0-521-57291-6)
  • Olaf Pedersen, A Survey of the Almagest, Odense University Press, 1974 (ISBN 87-7492-087-1)
  • Olaf Pedersen, Early Physics and Astronomy: A Historical Introduction, 2nd edition, Cambridge University Press, 1993 (ISBN 0-521-40340-5)

外部链接

[编辑]
检索自“https://zh.wikipedia.org/w/index.php?title=天文學大成&oldid=79911014”