弧度

提示：此条目的主题不是曲率。

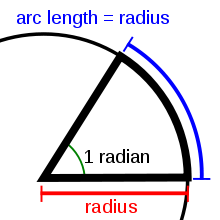單位弧度

常見的各種弧度

弧度（英語：radian）又稱弳度，符号$rad$，是平面角的一種計量單位，屬於國際單位制導出單位。單位弧度定義為圓弧長度等於半徑時的圓心角。因此在弧度制下，度量平面角的大小是以两射线交点为圆心的圆被射线所截的弧长与半径之比。

一個完整圓的弧度是$2\pi$，所以弧度制下的$1\pi$等於360度制下的180°。

轉換

以度數表示的角，把數字乘以${\frac {\pi }{180^{\circ }}}$便轉換成弧度；以弧度表示的角，乘以${\frac {180^{\circ }}{\pi }}$便轉換成度數。

$\pi =180^{\circ }$

$1={\frac {180^{\circ }}{\pi }}\approx 57.2958^{\circ }$

${\frac {\pi }{3}}={\frac {\pi }{3}}\cdot {\frac {180^{\circ }}{\pi }}=60^{\circ }$

$1^{\circ }=1^{\circ }\cdot {\frac {\pi }{180^{\circ }}}\approx 0.0175$

微積分學中，三角函數的角度要採用弧度為單位，以獲得正確的計算結果。

$\lim _{h\to 0}{\frac {\sin h}{h}}=1$

${\frac {d}{dx}}\sin x^{2}=2x\cos x^{2}$

把三角函數寫成泰勒级数，則必須以弧度表示。

一單位弳度等於一半徑長的弧所佔的角度

$\sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots \quad \!$

相同角度的轉換表

角度單位	值
轉	$0$	${\frac {1}{12}}$	${\frac {1}{8}}$	${\frac {1}{6}}$	${\frac {1}{4}}$	${\frac {1}{2}}$	${\frac {3}{4}}$	$1$
角度	$0^{\circ }$	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$90^{\circ }$	$180^{\circ }$	$270^{\circ }$	$360^{\circ }$
弧度	$0$	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi$	${\frac {3\pi }{2}}$	$2\pi$
梯度	$0^{g}$	$33{\frac {1}{3}}^{g}$	$50^{g}$	$66{\frac {2}{3}}^{g}$	$100^{g}$	$200^{g}$	$300^{g}$	$400^{g}$

參見

• 角度
• 球面度

參考文獻

• ISO 31-1
• ISO/IEC 80000-3

外部連結

• Radian （页面存档备份，存于互联网档案馆） at MathWorld
• 弧度 （页面存档备份，存于互联网档案馆） | [科學Online]