八元数

各种各样的數

基本

$\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}\sub\mathbb{R}\sub\mathbb{C}$ 自然數 $\begin{smallmatrix} \mathbb{N} \end{smallmatrix}$ 整數 $\begin{smallmatrix} \mathbb{Z} \end{smallmatrix}$ 二进分数 有限小数 循环小数 有理數 $\begin{smallmatrix} \mathbb{Q} \end{smallmatrix}$ 高斯整数 $\begin{smallmatrix} \mathbb{Z}[i] \end{smallmatrix}$ 代數數 $\begin{smallmatrix} \mathbb{A} \end{smallmatrix}$ 實數 $\begin{smallmatrix} \mathbb{R} \end{smallmatrix}$ 複數 $\begin{smallmatrix} \mathbb{C} \end{smallmatrix}$ 負數 分数 单位分数 无限小数 规矩数 無理數 超越數 二次无理数 虛數 艾森斯坦整数 $\begin{smallmatrix} \mathbb{Z}[\omega] \end{smallmatrix}$

延伸

雙複數 四元數 $\begin{smallmatrix} \mathbb{H} \end{smallmatrix}$ 共四元數 八元數 $\begin{smallmatrix} \mathbb{O} \end{smallmatrix}$ 超數 上超實數 超現實數 超複數 十六元數 $\begin{smallmatrix} \mathbb{S} \end{smallmatrix}$ 複四元數 大實數 超實數 $\begin{smallmatrix} {}^\star\mathbb{R} \end{smallmatrix}$

其他

对偶数 雙曲複數 序數 質數 同餘 可計算數 阿列夫数 公稱值 超限數 基數 P進數 規矩數 整數序列 數學常數 圓周率 $\begin{smallmatrix} \pi \end{smallmatrix}$ = 3.141592653… 自然對數的底 $\begin{smallmatrix} e \end{smallmatrix}$ = 2.718281828… 虛數單位 $\begin{smallmatrix} i \end{smallmatrix}$ = $\begin{smallmatrix} +\sqrt{-1} \end{smallmatrix}$ 無窮大 $\begin{smallmatrix} \infty \end{smallmatrix}$

八元数是四元数的一个非结合推广，通常记为O，或$\mathbb{O}$。

也许是因为八元数不提供一个结合性的乘法，它们比四元数引起较少的注意。尽管如此，八元数仍然与数学中的一些例外结构有关，其中包括例外李群。此外，八元数在诸如弦理论、狭义相对论和量子逻辑中也有应用。

歷史

八元數第一次被描述於1843年，於一封约翰·格雷夫斯給威廉·盧雲·哈密頓的信中。後來八元數由阿瑟·凯莱在1845年獨自發表。阿瑟·凯莱發表的八元數和约翰·格雷夫斯給威廉·盧雲·哈密頓的信中所提及的並無關係。

定义

八元数可以视为实数的八元组。每一个八元数都是单位八元数{1, i, j, k, l, il, jl, kl}的线性组合。也就是说，每一个八元数x都可以写成$x = x_0 + x_1\,i + x_2\,j + x_3\,k + x_4\,l + x_5\,il + x_6\,jl + x_7\,kl,$其中系数x_a是实数。

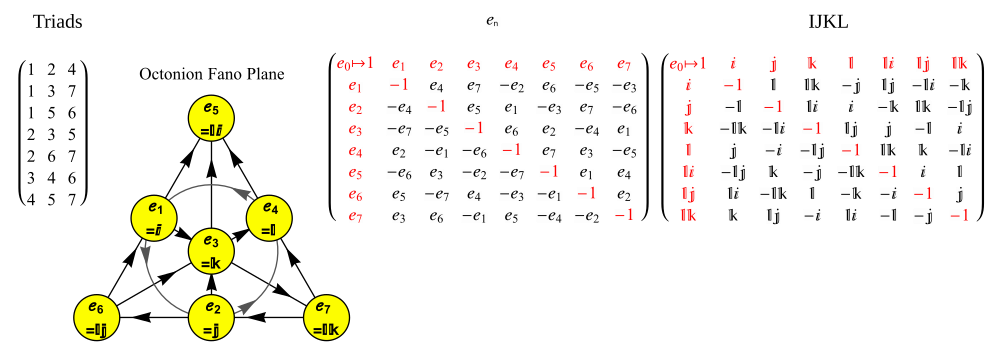
八元数的加法是把对应的系数相加，就像复数和四元数一样。根据线性，八元数的乘法完全由以下单位八元数的乘法表来决定。

1	i	j	k	l	il	jl	kl
i	−1	k	−j	il	−l	−kl	jl
j	−k	−1	i	jl	kl	−l	−il
k	j	−i	−1	kl	−jl	il	−l
l	−il	−jl	−kl	−1	i	j	k
il	l	−kl	jl	−i	−1	−k	j
jl	kl	l	−il	−j	k	−1	−i
kl	−jl	il	l	−k	−j	i	−1

凯莱-迪克松构造

一个更加系统的定义八元数的方法，是通过凯莱-迪克松构造。就像四元数可以用一对复数来定义一样，八元数可以用一对四元数来定义。两对四元数(a, b)和(c, d)的乘积定义为：

$(a,b)(c,d)=(ac-d^{*}b,da+bc^{*})$

其中$z^{*}$表示四元数z的共轭。这个定义与上面给出的定义是等价的。

法诺平面记忆

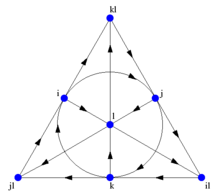
八元数的乘积的简单记忆。

一个用来记忆八元数的乘积的方便办法，由右面的图给出。这个图中有七个点和七条直线（经过i、j和k的圆也是一条直线），称为法诺平面。这些直线是有向的。七个点对应于Im(O)的七个标准基元素。每一对不同的点位于唯一的一条直线上，而每一条直线正好通过三个点。

设(a, b, c)为位于一条给定的直线上的三个有序点，其顺序由箭头的方向指定。那么，乘法由下式给出：

ab = c，ba = −c

以及它们的循环置换。这些规则与

• 1是乘法单位元，
• 对于图中的每一个点，都有$e^2=-1$

完全定义了八元数的乘法结构。七条直线的每一条都生成了O的一个子代数，与四元数H同构。

共轭、範数和逆元素

八元数

$x = x_0 + x_1\,i + x_2\,j + x_3\,k + x_4\,l + x_5\,il + x_6\,jl + x_7\,kl$

的共轭为：

$x^* = x_0 - x_1\,i - x_2\,j - x_3\,k - x_4\,l - x_5\,il - x_6\,jl - x_7\,kl.$

共轭是O的一个对合，满足$(xy)^{*}=y^{*}x^{*}$（注意次序的变化）。

x的实数部分定义为½(x + x^*) = x₀，虚数部分定义为½(x - x^*)。所有纯虚的八元数生成了O的一个七维子空间，记为Im(O)。

八元数x的範数定义为：

$\|x\| = \sqrt{x^{*} x}$

在这里，平方根是定义良好的，因为$x^{*}x=xx^{*}$总是非负实数：

$\|x\|^2 = x^{*}x = x_0^2 + x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 + x_6^2 + x_7^2$

这个範数与R⁸上的标准欧几里得範数是一致的。

O上範数的存在，意味着O的所有非零元素都存在逆元素。x ≠ 0的逆元素为：

$x^{-1} = \frac {x^*}{\|x\|^2}$

它满足$xx^{-1}=x^{-1}x=1$。

性质

八元数的乘法既不是交换的：

$ij = -ji \neq ji\,$

也不是结合的：

$(ij)l = -i(jl) \neq i(jl)\,$

然而，八元数确实满足结合性的一个较弱形式──交错性。这就是说，由任何两个元素所生成的子代数是结合的。实际上，我们可以证明，由O的任何两个元素所生成的子代数都与R、C或H同构，它们都是结合的。由于八元数不满足结合性，因此它们没有矩阵的表示法，与四元数不一样。

八元数确实保留了R、C和H共同拥有的一个重要的性质：O上的範数满足

$\|xy\| = \|x\|\|y\|$

这意味着八元数形成了一个非结合的赋範可除代数。所有由凯莱-迪克松构造所定义的更高维代数都不满足这个性质。它们都有零因子。

这样，实数域上唯一的赋範可除代数是R、C、H和O。这四个代数也形成了实数域上唯一的交错的、有限维的可除代数。

由于八元数不是结合的，因此O的非零元素不形成一个群。然而，它们形成一个拟群。

自同构

八元数的自同构A，是O的可逆线性变换，满足：

$A(xy) = A(x)A(y).\,$

O的所有自同构的集合组成了一个群，称为G₂。群G₂是一个单连通、紧致、14维的实李群。这个群是例外李群中最小的一个。

参见

• 双曲复数
• 四元数
• 十六元数
• Spin(8)
• PSL(2,7)──法诺平面的自同构群。

参考文献

• Baez, John, The Octonions, Bull. Amer. Math. Soc.. 2002, 39: 145-205 . Online HTML version at http://math.ucr.edu/home/baez/octonions/.
• Conway, John Horton; Smith, Derek A., On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd.. 2003, ISBN 1-56881-134-9 . (Review).