八元数

八元数是四元数的一个非结合推广，通常记为O，或$\mathbb {O}$。

也许是因为八元数不提供一个结合性的乘法，它们比四元数引起较少的注意。尽管如此，八元数仍然与数学中的一些例外结构有关，其中包括例外李群。此外，八元数在诸如弦理论、狭义相对论和量子逻辑中也有应用。

歷史

八元數第一次被描述於1843年，於一封约翰·格雷夫斯給威廉·盧雲·哈密頓的信中。後來八元數由阿瑟·凯莱在1845年獨自發表。阿瑟·凯莱發表的八元數和约翰·格雷夫斯給威廉·盧雲·哈密頓的信中所提及的並無關係。

定义

八元数可以视为实数的八元组。八元数有多種構造方式。以凯莱-迪克森结构為例，八元数可以表達為2個四元數P與Q的組合，即P+Q l或$p_{0}+p_{1}i+p_{2}j+p_{3}k+\left(q_{0}+q_{1}i+q_{2}j+q_{3}k\right)l\,$，其中，量l為其中一個八元数單位並滿足：

$i^{2}=j^{2}=k^{2}=l^{2}=-1\,$

在這種定義下每一个八元数都是单位八元数{1, i, j, k, l, il, jl, kl}的线性组合。也就是说，每一个八元数x都可以写成

$x=x_{0}+x_{1}\,i+x_{2}\,j+x_{3}\,k+x_{4}\,l+x_{5}\,il+x_{6}\,jl+x_{7}\,kl$

其中系数x_a是实数。 這些八元数單位亦滿足：

$i^{2}=j^{2}=k^{2}=l^{2}=(il)^{2}=(jl)^{2}=(kl)^{2}=-1\,$

八元数的加法是把对应的系数相加，就像复数和四元数一样。根据线性，八元数的乘法完全由以下单位八元数的乘法表来决定。

$\times$	$1$	$i$	$j$	$k$	$l$	$il$	$jl$	$kl$
$1$	$1$	$i$	$j$	$k$	$l$	$il$	$jl$	$kl$
$i$	$i$	$-1$	$k$	$-j$	$il$	$-l$	$-kl$	$jl$
$j$	$j$	$-k$	$-1$	$i$	$jl$	$kl$	$-l$	$-il$
$k$	$k$	$j$	$-i$	$-1$	$kl$	$-jl$	$il$	$-l$
$l$	$l$	$-il$	$-jl$	$-kl$	$-1$	$i$	$j$	$k$
$il$	$il$	$l$	$-kl$	$jl$	$-i$	$-1$	$-k$	$j$
$jl$	$jl$	$kl$	$l$	$-il$	$-j$	$k$	$-1$	$-i$
$kl$	$kl$	$-jl$	$il$	$l$	$-k$	$-j$	$i$	$-1$

一些不同的定義方式會將八元數的單位元素表達為e_a的線性組合，其中 a=0, 1,..., 7 ：

$\{e_{0},e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7}\},$

每個八元數單位元素皆不相等，而其平方為實數。也就是說，每個八元數 x 都可以寫成以下形式：

$x=x_{0}e_{0}+x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}+x_{4}e_{4}+x_{5}e_{5}+x_{6}e_{6}+x_{7}e_{7},\,$

其中x_i為實數的係數。八元數的加法和減法是通過加減相應的項以及它們的係數來完成的，與四元數的加減法類似。 乘法則較為複雜。 八元數的乘法是對加法的分配，所以兩個八元數的乘積可以通過對所有項的乘積求和來計算，再次如同四元數一般。 每對項的乘積可以通過係數的乘積和單位八元數的乘法表給出，其乘法表的結構與{1, i, j, k, l, il, jl, kl}的模式（$p_{0}+p_{1}i+p_{2}j+p_{3}k+\left(q_{0}+q_{1}i+q_{2}j+q_{3}k\right)l\,$）類似。這個乘法表先後由Graves於1843年和Cayley於1845年描述：

$e_{i}e_{j}$		$e_{j}$
		$e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
$e_{i}$	$e_{0}$	$e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
	$e_{1}$	$e_{1}$	$-e_{0}$	$e_{3}$	$-e_{2}$	$e_{5}$	$-e_{4}$	$-e_{7}$	$e_{6}$
	$e_{2}$	$e_{2}$	$-e_{3}$	$-e_{0}$	$e_{1}$	$e_{6}$	$e_{7}$	$-e_{4}$	$-e_{5}$
	$e_{3}$	$e_{3}$	$e_{2}$	$-e_{1}$	$-e_{0}$	$e_{7}$	$-e_{6}$	$e_{5}$	$-e_{4}$
	$e_{4}$	$e_{4}$	$-e_{5}$	$-e_{6}$	$-e_{7}$	$-e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$
	$e_{5}$	$e_{5}$	$e_{4}$	$-e_{7}$	$e_{6}$	$-e_{1}$	$-e_{0}$	$-e_{3}$	$e_{2}$
	$e_{6}$	$e_{6}$	$e_{7}$	$e_{4}$	$-e_{5}$	$-e_{2}$	$e_{3}$	$-e_{0}$	$-e_{1}$
	$e_{7}$	$e_{7}$	$-e_{6}$	$e_{5}$	$e_{4}$	$-e_{3}$	$-e_{2}$	$e_{1}$	$-e_{0}$

凯莱-迪克松构造

一个更加系统的定义八元数的方法，是通过凯莱-迪克松构造。就像四元数可以用一对复数来定义一样，八元数可以用一对四元数来定义。两对四元数(a, b)和(c, d)的乘积定义为：

$(a,b)(c,d)=(ac-d^{*}b,da+bc^{*})$

其中$z^{*}$表示四元数z的共轭。这个定义与上面给出的定义是等价的。

法诺平面记忆

八元数的乘积的简单记忆。

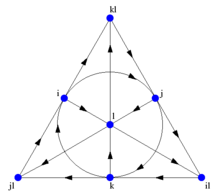
一个用来记忆八元数的乘积的方便办法，由右面的图给出。这个图中有七个点和七条直线（经过i、j和k的圆也是一条直线），称为法诺平面。这些直线是有向的。七个点对应于Im(O)的七个标准基元素。每一对不同的点位于唯一的一条直线上，而每一条直线正好通过三个点。

设(a, b, c)为位于一条给定的直线上的三个有序点，其顺序由箭头的方向指定。那么，乘法由下式给出：

ab = c，ba = −c

以及它们的循环置换。这些规则与

• 1是乘法单位元，
• 对于图中的每一个点，都有$e^{2}=-1$

完全定义了八元数的乘法结构。七条直线的每一条都生成了O的一个子代数，与四元数H同构。

共轭、範数和逆元素

八元数

$x=x_{0}+x_{1}\,i+x_{2}\,j+x_{3}\,k+x_{4}\,l+x_{5}\,il+x_{6}\,jl+x_{7}\,kl$

的共轭为：

$x^{*}=x_{0}-x_{1}\,i-x_{2}\,j-x_{3}\,k-x_{4}\,l-x_{5}\,il-x_{6}\,jl-x_{7}\,kl.$

共轭是O的一个对合，满足$(xy)^{*}=y^{*}x^{*}$（注意次序的变化）。

x的实数部分定义为½(x + x^*) = x₀，虚数部分定义为½(x - x^*)。所有纯虚的八元数生成了O的一个七维子空间，记为Im(O)。

八元数x的範数定义为：

$\|x\|={\sqrt {x^{*}x}}$

在这里，平方根是定义良好的，因为$x^{*}x=xx^{*}$总是非负实数：

$\|x\|^{2}=x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}$

这个範数与R⁸上的标准欧几里得範数是一致的。

O上範数的存在，意味着O的所有非零元素都存在逆元素。x ≠ 0的逆元素为：

$x^{-1}={\frac {x^{*}}{\|x\|^{2}}}$

它满足$xx^{-1}=x^{-1}x=1$。

性质

八元数的乘法既不是交换的：

$ij=-ji\neq ji\,$

也不是结合的：

$(ij)l=-i(jl)\neq i(jl)\,$

然而，八元数确实满足结合性的一个较弱形式──交错性。这就是说，由任何两个元素所生成的子代数是结合的。实际上，我们可以证明，由O的任何两个元素所生成的子代数都与R、C或H同构，它们都是结合的。由于八元数不满足结合性，因此它们没有矩阵的表示法，与四元数不一样。

八元数确实保留了R、C和H共同拥有的一个重要的性质：O上的範数满足

$\|xy\|=\|x\|\|y\|$

这意味着八元数形成了一个非结合的赋範可除代数。所有由凯莱-迪克松构造所定义的更高维代数都不满足这个性质。它们都有零因子。

这样，实数域上唯一的赋範可除代数是R、C、H和O。这四个代数也形成了实数域上唯一的交错的、有限维的可除代数。

由于八元数不是结合的，因此O的非零元素不形成一个群。然而，它们形成一个拟群。

自同构

八元数的自同构A，是O的可逆线性变换，满足：

$A(xy)=A(x)A(y).\,$

O的所有自同构的集合组成了一个群，称为G₂。群G₂是一个单连通、紧致、14维的实李群。这个群是例外李群中最小的一个。

参见

• 双曲复数
• 四元数
• 十六元数
• Spin(8)
• PSL(2,7)──法诺平面的自同构群。

参考文献

• Baez, John, The Octonions, Bull. Amer. Math. Soc., 2002, 39: 145–205 [2008-12-01], （原始内容存档于2008-12-09） . Online HTML version at https://web.archive.org/web/20081009232658/http://math.ucr.edu/home/baez/octonions/.
• Conway, John Horton; Smith, Derek A., On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., 2003, ISBN 1-56881-134-9 . (Review（页面存档备份，存于互联网档案馆）).