法拉第电磁感应定律

法拉第電磁感應定律(英語:Faraday's law of electromagnetic induction)常直接簡稱為“法拉第定律”,是電磁學的一條基本定律,也是變壓器、電感元件及多種電動機、發電機、螺線管的根本運作原理。定律指出:[1]
| “ | 任何封閉电路中感应电动势大小,等於穿过这一电路磁通量的变化率。 | ” |
此定律预测磁场如何与电路相互作用以产生电动势,这种现象称为电磁感应。
虽然約瑟·亨利在1830年的獨立研究中比法拉第早發現這一定律,但其並未發表;迈克尔·法拉第则于1831年發現此定律,命名為法拉第定律。
本定律可用以下的公式表达:[2]
其中:
電動勢的方向(公式中的負號)由楞次定律提供。“通過電路的磁通量”的意義會由下面的例子闡述。
傳統上有兩種改變通過電路的磁通量的方式。至於感應電動勢時,改變的是自身的電場,例如改變生成場的電流(就像變壓器那樣)。而至於動生電動勢時,改變的是磁場中的整個或部份電路的運動,例如像在同極發電機中那樣。

用詞[编辑]
電磁感應現象不應與靜電感應混淆。電磁感應將電動勢與通過電路的磁通量聯繫起來,而靜電感應則是使用另一帶電荷的物體使物體產生電荷的方法。
馬克士威-法拉第方程[编辑]
本節是一段題外話,作用是區分本條目中的“法拉第定律”及麥克斯韋方程組中用同一個名字的∇×E方程。於本條目中∇×E方程會被稱為馬克士威-法拉第方程。
馬克士威於1855年總結出法拉第定律的旋度版本,而黑維塞則於1884年將定律重寫成旋度方程:
其中
方程的意義是,如果電場的空間依賴在紙面上成逆時針方向(經右手定則,得旋度向量方向為出紙面),那麼磁場會因時間而更少指出紙面,更多地指入頁面(跟旋度向量異號)。方程跟磁場的變量有關係。故磁場不一定要指向紙面,只需向該方向轉動即可。
本方程(在本條目中被稱為馬克士威-法拉第方程)是馬克士威方程組的四條方程之一。
在麥克斯韋-法拉第方程中,黑維塞用的是時間偏導數。不使用馬克士威用過的時間全導數,而使用時間偏導數,這樣做使得馬克士威-法拉第方程不能說明動生電動勢。[註 1]。然而,馬克士威-法拉第方程很多時候會被直接稱為“法拉第定律”。[3]
在本條目中“法拉第定律”一詞指的是通量方程,而“馬克士威-法拉第方程”指的則是黑維塞的旋度方程,也就是現在的馬克士威方程組中的那一條。
通過表面的磁通量及圈中的電動勢[编辑]


法拉第電磁感應定律用到通過一表面Σ的磁通量ΦB,其積分形式定義如下:
其中dA為移動面Σ(t)的面積元,B為磁場,B·dA為向量點積。見圖一。更多細節見面積分及磁通量條目。設該表面有一個開口,邊界為閉合曲線∂Σ(t)。見圖二。
當通量改變時,把一電荷在閉合曲線中∂Σ(t)移一圈(每單位電荷)所作的功,也就是電動勢,可由法拉第電磁感應定律求得:
其中:
設有一緊纏線圈,法拉第電磁感應定律指出:
- 其中N為線圈圈數;
- ΦB為通過一圈的磁通量,單位為韋伯。
在選擇路徑∂Σ(t)求電動勢時,路徑須滿足兩個基本條件:(一)路徑閉合;(二)路徑必需能描述到電路各部分的相對運動(這就是∂Σ(t)中變量為時間的原因)。路徑並不一定要跟隨電流的流動路線,但用通量定律求出的電動勢,理所當然地會是通過所選路徑的電動勢。假若路徑並不跟隨電流的話,那麼那電動勢可能不是驅動着電流的那一電動勢。
例一:空間變強磁場[编辑]
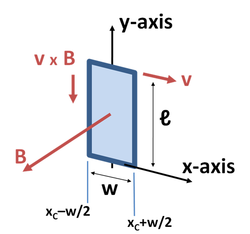
考慮圖三的長方形線圈,它在xy平面上向x方向以速率v移動。因此,線圈中心xC滿足v = dxC/dt。線圈在y方向的長度為ℓ,x方向的寬度為w。一不隨時間改變,而隨x方向改變的磁場B(x)指向z方向。左邊的磁場為B(xC − w/2),右邊的磁場為B(xC + w/2)。電動勢可直接求得,或由上述的法拉第電磁感應定律求得。
洛倫茲力法[编辑]
在線圈左邊的一電荷q,所受的洛倫茲力為qv×Bk = −qvB(xC − w/2)j(j、k分別為y方向及z方向的單位向量,見向量積),因此左邊整段電線的電動勢(單位電荷所作的功)為vℓB(xC − w/2)。可用相同的論述,求出右邊電線的電動勢為vℓB(xC + w/2)。兩股電動勢互相抵抗,將正電荷推向線圈底部。由於這時磁場的強度會向x方向增強,所以右邊的力最強,電流會順時針流動:使用右手定則,電流所產生的磁場會抵抗外加的磁場。[註 2]驅動電流的電動勢必須向逆時針方向增加(抵抗電流)。把電動勢向逆時針方向加起來得:
法拉第定律法[编辑]
線圈上任何位置通過線圈的磁通量為
其正負取決於表面的垂直線與B的方向之異同。如果表面垂直線跟感應電流的B同一方向,式子為負。此時通量的時間導數(使用微分的鏈式法則或萊布尼茨定則的通用形式求出)為:
(其中v = dxC/dt為線圈於x方向的運動速率),所以
跟之前一樣。
這兩種方法一般來說都一樣,但視乎例子而定,其中一種有時可能會比較實用。
例二:均勻磁場中的運動環路[编辑]

圖四為由上下兩塊帶導電邊沿的碟片所組成的轉軸,上面的電線環路垂直地連接着兩塊碟片。整組裝置在磁場中旋轉,該磁場向外呈放射狀指出,但其大小不隨方向變化。一向外的回路從邊沿上把電流收集起來。在收集迴路的位置上,向外的磁場與回路位於同一個平面上,因此收電回路並不對電路的磁通量造成影響。電動勢可直接求出,或使用上文的法拉第定律求出。
洛倫茲力法[编辑]
這個案中,在移動環路中那兩根垂直的電線裏,洛倫茲力向下驅動着電流,因此電流從上碟片流向下碟片。在碟片的導電邊沿內,洛倫茲力與邊沿垂直,所以邊沿上並沒有電動勢,環路中的水平部分也沒有。電流通過外加的回路從下邊沿傳到上邊沿,而該回路位於磁場的平面上。因此,回路中的洛倫茲力與回路平行,在這回路中並沒有生成電動勢。穿過電流通道,到達電流反方向流動的地方,功只在移動環路垂直電線中抵抗洛倫茲力,其中
因此電動勢為
其中ℓ為環路中的垂直長度,與角轉動率相關的速度可由v = r ω求出,而r = 碟片半徑。注意,在任何跟環路轉動並連接上下邊沿的路徑中,所作的功都一樣。
法拉第定律法[编辑]
一個直覺上很吸引但錯誤的通量定則使用法是,將通過電流的通量當成只是ΦB = Bwℓ,其中w為移動環路的寬度。這數目與時間沒有關係,所以這方法會不正確地預測出無生成電動勢。這套論述的缺陷在於它並沒有考慮到整個電路,而整個電路是閉合的環路。
使用通量定則時,我們必須顧及整個電路,其中包括通過上下碟片邊沿的路徑。我們可以選擇一通過兩道邊沿及移動環路的任意閉合路徑,而通量定則會找出該路徑的電動勢。任何有一部分連接移動環路的路徑,都會表達到電路移動部分的相對運動。
作為一個路徑例子,選擇在上碟片按照轉動方向,並下碟片按照轉動反方向穿過電路(由圖四的箭號表示)。在這情況下,對與回路成角θ的移動環路而言,圓柱體的一部分面積A = rℓθ為電路的一部分。這面積與磁場垂直,所以造成了這個大小的通量:
其中式子為負,這是因為右手定則指出,電流環路所產生的磁場,與外加的磁場方向相反的緣故。由於這是通量中唯一一個跟隨時間轉變的部分,所以通量定則預測的電動勢為
與使用洛倫茲力法的計算答案一致。
現在嘗試不同的路徑。跟隨一條選擇餘下部分通過邊沿的路徑。那麼耦合磁通量會隨θ增加而減少,但右手定則會指出把電流環路加到外加磁場上去,因此這條路徑跟第一條路徑的電動勢相同。任何回路的組合都會對電動勢產生相同的結果,因此跟隨哪一條路徑實際上並不重要。
直接從通量變量中推導[编辑]

以上使用閉合路徑求電動勢的方法,看起來是取決於路徑幾何的細節。相反地,使用勞侖茲力則沒有這樣的限制。所以有需要加深對通量定則的理解,有關路徑等同及路徑選取時的會漏掉的細節。
圖五是圖四的理想化版本,當中圓柱體被展開成了平面。同樣的路徑分析依然有效,但是還有一個可以簡化的地方。電路中與時間無關的方面,並不能夠影響通量隨時間的變化率。例如,環路以均速滑動時,電流通過環路流動的細節,並不取決於時間。與其考慮求電動勢時環路選取的細節,不如考慮環路移動時所掃過的磁場面積。這相當於找出電路通量的切斷率。[註 3]這個說法提供了一個方法,可直接求出通量變化率,而不需要考慮電路上各種路徑選取,隨時間而變化的細節。跟使用洛倫茲力一樣,很明顯地,任何兩條連接移動環路的路徑,都會產生相同的通量變化率,不同之處只在於它們如何與環路相交。
圖五中,單位時間內掃過的面積為dA/dt = vℓ,跟選取的環路細節無關,所以可經法拉第電磁感應定律求出電動勢:[註 4]
電路勢的路徑的不依賴性表明,如果滑動環路被實心導電板所取代,又或是更複雜的某種變形表面,分析都是一樣的:找出電路移動部分掃過面積的通量。相近地,如果圖四的移動環路被一360°的實心導電圓柱體所取代,掃過面積的計算就跟只有一個環路時是完全一樣的。故此,對圓柱體及實心導電板的個案而言,法拉第定律所預測的電動勢完全一樣,更甚者,以有孔板為壁的圓柱體的個案也一樣。但是注意,這個電動勢所導致的流動電流是不一樣的,因為電阻決定電流。
麥克斯韋-法拉第方程[编辑]

變化中的磁場會生成電場;這個現象由麥克斯韋-法拉第方程描述:[註 5]
其中:
這條方程是現代麥克斯韋方程組內的其中一條,很多時候被稱為法拉第定律。然而,由於它只含有一個時間偏導數,它的應用只限於在隨時間變化的磁場中靜止電荷的情況。它並不能說明帶電粒子在磁場中移動的電磁感應狀況。
它可以用開爾文-斯托克斯定理寫成積分形式:[4]
其中把導數移至積分前這個動作,需要一與時無關的曲面Σ(在這裏被視為偏導數解釋的一部分),見圖六:
- Σ為一被閉合圍道∂Σ包圍的曲面;Σ與∂Σ皆為固定的,不隨時間變動;
- E為電場強度;
- dℓ為圍道∂Σ的一無限小向量元;
- B為磁通量密度;
- dA為曲面Σ的一無限小向量元,其大小相等於一塊無限小曲面,而其方向與該塊曲面成正交。
dℓ和dA都具有正負模糊性;要得到正確的正負號,需要使用右手定則,解釋詳見開爾文-斯托克斯定理條目。對一平面Σ而言,曲線∂Σ的正路徑元dℓ,其定義由右手定則所規定,就是當右手姆指跟表面Σ的垂直線n同一方向時,其他手指所指的那一個方向。
圍繞着∂Σ的積分叫曲線積分或路徑積分。麥克斯韋-法拉第方程右邊的曲面積分,是通過Σ的磁通量ΦB的明確表達式。注意E的非零路徑積分,跟電荷產生電場的表現不一樣。由電荷生成的電場能以標量場的梯度表達,為泊松方程的解,並且路徑積分為零。見梯度定理。
積分方程對通過空間的任何路徑∂Σ成立,也對任何以該路徑為邊界的的表面Σ成立。注意,但是已知在這方程裏,∂Σ及Σ都不隨時間而改變。這個積分形式不能用於運動電動勢,因為Σ跟時間無關。注意這方程內並沒有電動勢 ,所以確實不能夠在不引入洛倫茲力的情況下計算出功。

使用完整的洛倫茲力計算電動勢:
法拉第電磁感應定律的一個描述,比麥克斯韋-法拉第方程的積分形式更通用(見洛倫茲力),如下:
其中∂Σ(t)為圍着運動表面Σ(t)的閉合路徑,而v為運動速率。見圖二。注意上面用的是時間常導數,而不是時間偏導數,意指Σ(t)的時間差異必須被微分所包括。被積函數中,曲線dℓ的元以速率v移動。
圖七為磁力是如何促成電動勢作出了詮釋,而電動勢就在上面方程的左邊。曲線∂Σ部分dℓ,在時間dt以速率v移動時掃過的面積為(見向量積的幾何意義):
所以在時間dt間通過∂Σ為邊的表面中這一部分的磁通量變量ΔΦB為:
如果我們把這些通過所有部分dℓ的ΔΦB的作用加在一起,就可以得到法拉第定律對磁力的促成作用。也就是,這個項跟運動電動勢有關係。
例三:移動觀測者的視點[编辑]
再次討論圖三的例子,但這次以移動觀測者的參考系,帶出電場與磁場間以及運動與感應電動勢的密切關係。[註 6]假設一環路觀測者與環路一起移動。觀測者以洛倫茲力及法拉第電磁感應定律計算環路的電動勢。由於這觀測者與環路一起移動,觀測者看不到環路的運動,以及零v×B。然而,由於磁場隨x位置變化,所以觀測者看到時間變強的磁場,也就是:
其中k為指向z方向的單位向量。[註 7]
洛倫茲力定律版本[编辑]
麥克斯韋-法拉第方程指出移動觀測者在y方向所見的電場Ey可由下式表示(見旋度):
下式使用了鏈鎖律:
求解Ey,準確到一個對環路積分沒有作用的常數,得:
使用洛倫茲力定律,得一個電場分量,觀測者於時間t得環路的電動勢為:
這個結果跟靜止觀測者的個案一致,他看到的是中點xC移到xC + vt。然而,移動觀測者的結果中,洛倫茲力看起來只有電分量,而靜止觀測者的則只有磁分量。
法拉第電磁感應定律[编辑]
使用法拉第電磁感應定律,與xC一起移動的觀測者看到磁通量的變化,但環路看起來並沒有移動:環路的中心xC被固定了,這是因為觀測者與環路一起移動着。通量則是:
其中右式為負,這是因為表面的垂直線與外加磁場各自指向相反的方向。現在從法拉第電磁感應定律得出的電動勢是:
答案是一樣的。時間導數走進了積分裏面,這是因為積分的上下限並不取決於時間。又一次,鏈式定律被用於把時間導數轉化成x導數。
靜止觀測者認為該電動勢是運動電動勢,而移動觀測者則認為是感應電動勢。[5]
作為兩種不同現象的法拉第定律[编辑]
有些物理學家注意到法拉第定律是一條描述兩種現象的方程式:由磁力在移動中的電線中產生的動生電動勢,及由磁場轉變而成的電力所產生的感應電動勢。就像理查德·費曼指出的那樣:[6]
所以“通量定則”,指出電路中電動勢等於通過電路的磁通量變化率的,同樣適用於通量不變化的時候,這是因為場有變化,或是因為電路移動(或兩者皆是)……但是在我們對定則的解釋裏,我們用了兩個屬於完全不同個案的定律:“電路運動”的和“場變化”的。
我們不知道在物理學上還有其他地方,可以用到一條如此簡單且準確的通用原理,來明白及分析兩個不同的現象。
— 理查德·P·費曼 《費曼物理學講義》
格里夫斯的書中也有類似陳述。[7]
歷史[编辑]
法拉第定律最初是一條基於觀察的實驗定律。[8][9]後來被正式化,其偏導數的限制版本,跟其他的電磁學定律一塊被列麥克斯韋方程組的現代黑維塞版本。
法拉第電磁感應定律是基於法拉第於1831年所作的實驗。這個效應被約瑟·亨利於大約同時發現,但法拉第的發表時間較早。[10][11]
見麥克斯韋討論電動勢的原著。[12]
於1834年由波羅的海德國科學家海因里希·楞次發現的楞次定律,提供了感應電動勢的方向,及生成感應電動勢的電流方向。
應用[编辑]
發電機[编辑]

由法拉第電磁感應定律因電路及磁場的相對運動所造成的電動勢,是發電機背後的根本現象。當永久性磁鐵相對於一導電體運動時(反之亦然),就會產生電動勢。如果電線這時連着電負載的話,電流就會流動,並因此產生電能,把機械運動的能量轉變成電能。例如,基於圖四的鼓輪發電機。另一種實現這種構想的發電機就是法拉第碟片,簡化版本見圖八。注意使用圖五的分析,或直接用洛倫茲力定律,都能得出使用實心導電碟片運作不變的這一結果。
在法拉第碟片這一例子中,碟片在與碟片垂直的均勻磁場中運動,導致一電流因洛倫兹力流到向外的軸臂裏。明白機械運動是如何成為驅動電流的必需品,是很有趣的一件事。當生成的電流通過導電的邊沿時,這電流會經由安培環路定理生成出一磁場(圖八中標示為“Induced B”)。因此邊沿成了抵抗轉動的電磁鐵(楞次定律一例)。在圖的右邊,經轉動中軸臂返回的電流,通過右邊沿到達底部的電刷。此一返回電流所感應的磁場會抵抗外加的磁場,它有減少通過電路那邊通量的傾向,以此增加旋轉帶來的通量。因此在圖的左邊,經轉動中軸臂返回的電流,通過左邊沿到達底部的電刷。感應磁場會增加電路這邊的通量,減少旋轉帶來的通量。所以,電路兩邊都生成出抵抗轉動的電動勢。儘管有反作用力,需要保持碟片轉動的能量,正等於所產生的電能(加上由於摩擦、焦耳熱及其他消耗所浪費的能量)。所有把機械能轉化成電能的發電機都會有這種特性。
雖然法拉第定律經常描述發電機的運作原理,但是運作的機理可以隨個案而變。當磁鐵繞着靜止的導電體旋轉時,變化中的磁場生成電場,就像麥克斯韋-法拉第方程描述的那樣,而電場就會通過電線推着電荷行進。這個案叫感應電動勢。另一方面,當磁鐵靜止,而導電體運動時,運動中的電荷的受到一股磁力(像洛倫茲力定律所描述的那樣),而這磁力會通過電線推着電荷行進。這個案叫動生電動勢。(更多有關感應電動勢、動生電動勢、法拉第定律及洛倫茲力的細節,可見上例或格里夫斯一書。[13])
電動機[编辑]
發電機可以“反過來”運作,成為電動機。例如,用法拉第碟片這例子,設一直流電流由電壓驅動,通過導電軸臂。然後由洛倫茲力定律可知,行進中的電荷受到磁場B的力,而這股力會按佛來明左手定則訂下的方向來轉動碟片。在沒有不可逆效應(如摩擦或焦耳熱)的情況下,碟片的轉動速率必需使得dΦB/dt等於驅動電流的電壓。
變壓器[编辑]
法拉第定律所預測的電動勢,同時也是變壓器的運作原理。當線圈中的電流轉變時,轉變中的電流生成一轉變中的磁場。在磁場作用範圍中的第二條電線,會感受到磁場的轉變,於是自身的耦合磁通量也會轉變(dΦB/dt)。因此,第二個線圈內會有電動勢,這電動勢被稱為感應電動勢或變壓器電動勢。如果線圈的兩端是連接着一個電負載的話,電流就會流動。
電磁流量計[编辑]
法拉第定律可被用於量度導電液體或漿狀物的流動。這樣一個儀器被稱為電磁流量計。在磁場B中因導電液以速率為v的速度移動,所生成的感應電壓ε可由以下公式求出:
其中ℓ為電磁流量計中電極間的距離。
另見[编辑]
註解[编辑]
- ^ 為何這條方式不能解釋動生電動勢的解釋可見於Griffiths Introduction to Electrodynamics, pp.301-3, or Feynman Lectures on Physics, Ch. II-17
- ^ 感應電流產生的磁場有減低磁通量的傾向,而線圈的運動則有增加它的傾向(因為B(x)會隨線圈移動而增加)。抵抗運動是勒沙特列原理一個例子,以楞次定律這個形式進行的。
- ^ 這個說法指的是法拉第力的線。
- ^ 當移動環路通過收集環路時,掃出的通量由減少變成增加。同一時間,電流的轉向由逆時針變成順時針,因此磁場生成的電流會抵抗通量的變化。相應地,法拉第定律dΦB/dt的正負也會由原本的負,轉成了正,跟通量轉變的正負剛好相反,所以不論收集點在移動環路的哪一邊,電動勢都是正的。
- ^ “麥克斯韋-法拉第方程”一詞很多時候會由“法拉第電磁感應定律”或甚至“法拉第定律”所取代。後面兩個詞有多重意思,所以這裏用“麥克斯韋-法拉第方程”來防止混淆。
- ^ 在這一例子中,假定速率遠低於光速,因此場變換時由洛倫茲變換所造成的修正值可以被忽略。
- ^ 其中一個可得到這結果的方法是,在移動參考系中從xC量度x,假設ξ = x - xC ( t )。然後於時間t,移動觀測者看到場B( ξ, t ),而靜止觀測者在同一個地方看到場,B [ ξ + xC ( t ) ] = B ( ξ + xC0 + v t ),其中xC0 = xC ( t = 0 )。
資料來源[编辑]
- ^ M N O Sadiku. Elements of Electromagnetics Fourth Edition. NY/Oxford UK: Oxford University Press. 2007: §9.2 pp. 386 ff. ISBN 0-19-530048-3.
- ^ Tai L. Chow. Electromagnetic theory. Sudbury MA: Jones and Bartlett. 2006. Chapter 5; p. 171 ff [2008-12-25]. ISBN 0-7637-3827-1. (原始内容存档于2011-07-22).
- ^ 見Griffiths Introduction to Electrodynamics pp. 301-3 或 Feynman Lectures on Physics Ch. II-17。 這兩位作者都用“通量定則”這個詞來聯繫通量及電動勢,而把旋量版本叫做“法拉第定律”。還有其他叫法,在Jackson的Classical Electrodynamics中,兩條定律分別被稱為“法拉第定律的積分形式”及“法拉第定律的微分形式”。
- ^ Roger F Harrington. Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. 2003: 56. ISBN 0486432416.
- ^ Peter Alan Davidson. An Introduction to Magnetohydrodynamics. Cambridge UK: Cambridge University Press. 2001: 44. ISBN 0521794870.
- ^ 費曼把聯繫磁通量及電動勢的定律叫“通量定則”。Richard Phillips Feynman, Leighton R B & Sands M L. The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. 2006. Vol. II, pp. 17-2. ISBN 0805390499.
- ^ Griffiths, David J. Introduction to Electrodynamics Third Edition. Upper Saddle River NJ: Prentice Hall. 1999: 301-3 [2009-01-10]. ISBN 0-13-805326-X. (原始内容存档于2019-10-29).. 注意把通量及電動勢聯繫起來的定律,在本條目中被稱為“法拉第定律”,而格里夫斯則用上“通用通量定則”一詞。而格里夫斯則把本條目中的“麥克斯韋-法拉第定律”,叫做“法拉第定律”。所以實際上,在教科書中,格里夫斯的陳述是有關“通用通量定則”的。
- ^ BB Laud. Electromagnetics. New Delhi: New Age International. 1987: 151. ISBN 0852264992.
- ^ L. Pearce Williams. The Origins of Field Theory. Random House. 1966: 77-78, 133 (for electromagnetic induction) ; p. 85-89, 133 (for electrostatic induction).
- ^ Ulaby, Fawwaz. Fundamentals of applied electromagnetics 5th Edition. Pearson:Prentice Hall. 2007: 255 [2008-12-26]. ISBN 0-13-241326-4. (原始内容存档于2020-10-30).
- ^ Joseph Henry. Distinguished Members Gallery, National Academy of Sciences. [2006-11-30]. (原始内容存档于2006-12-09).
- ^ James Clerk Maxwell. A treatise on electricity and magnetism v. 2. Oxford UK: Clarendon Press. 1881. Chapter III, §530, p. 178. ISBN 0486606376.
- ^ Griffiths, David J. Introduction to Electrodynamics Third Edition. Upper Saddle River NJ: Prentice Hall. 1999: 301-303 [2009-01-10]. ISBN 0-13-805326-X. (原始内容存档于2019-10-29).
延伸閱讀[编辑]
有關法拉第定律一詞各種用法的討論: Tankersley and Mosca: Introducing Faraday's law (英文)
外部連結[编辑]
- 電磁感应的簡易互動Java教學 美國國家高能磁場實驗室 (英文)
- R. Vega 《電磁感應:法拉第定律與楞次定律》——高度動畫化課堂 (英文)
- 喬治亞州州立大學超物理筆記 (页面存档备份,存于互联网档案馆); 另見 主頁 (页面存档备份,存于互联网档案馆) (英文)
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||












![{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec1ba6719fecd0f5dd9e698b5f699a6553b4b3bf)


![{\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/41ddaf1f754720997a3191b66d98a1752c1b851b)
![{\displaystyle =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28f3c376811d459217a55a67a7ebfb88e4588438)
![{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bfbb47d0853b397d5c9f557428ea03d597d1f8f)


















![{\displaystyle {\mathcal {E}}=-\ell [E_{y}(x_{C}+w/2,\ t)-E_{y}(x_{C}-w/2,\ t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c3c17ff369123ebc572ae50480462b519144ee)
![{\displaystyle =v\ell [B(x_{C}+w/2+vt)-B(x_{C}-w/2+vt)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce2682b1ed2c655dce13e6eb516a845a9a931f8c)



![{\displaystyle =v\ell \ [B(x_{C}+w/2+vt)-B(x_{C}-w/2+vt)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8709d49795f14344e93367422b590c5750e69ca)




