卷积、互相关 和自相关 的图示比较。运算涉及函数
f
{\displaystyle f}
f
{\displaystyle f}
f
{\displaystyle f}
g
∗
f
{\displaystyle g*f}
f
⋆
g
{\displaystyle f\star g}
在泛函分析 中,捲積 (convolution),或译为疊積 、褶積 或旋積 ,是透過两个函数
f
{\displaystyle f}
g
{\displaystyle g}
算子 ,表徵函数
f
{\displaystyle f}
g
{\displaystyle g}
区间 的指示函数 ,卷积还可以被看作是“滑動平均 ”的推廣。
卷积是数学分析 中一种重要的运算。设:
f
(
t
)
{\displaystyle f(t)}
g
(
t
)
{\displaystyle g(t)}
实数
R
{\displaystyle \mathbb {R} }
可积函数 ,定义二者的卷积
(
f
∗
g
)
(
t
)
{\displaystyle (f*g)(t)}
积分 变换 :
(
f
∗
g
)
(
t
)
≜
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
d
τ
{\displaystyle (f*g)(t)\triangleq \int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,\mathrm {d} \tau }
(
f
∗
g
)
(
t
)
{\displaystyle (f*g)(t)}
(
f
∗
g
)
(
t
)
≜
∫
−
∞
∞
f
(
t
−
τ
)
g
(
τ
)
d
τ
=
(
g
∗
f
)
(
t
)
{\displaystyle (f*g)(t)\triangleq \int _{-\infty }^{\infty }f(t-\tau )g(\tau )\,d\tau =(g*f)(t)}
函数
f
{\displaystyle f}
g
{\displaystyle g}
支撑 在
[
0
,
∞
]
{\displaystyle [0,\infty ]}
(
f
∗
g
)
(
t
)
=
∫
0
t
f
(
τ
)
g
(
t
−
τ
)
d
τ
{\displaystyle (f*g)(t)=\int _{0}^{t}f(\tau )g(t-\tau )\,d\tau \quad }
f
,
g
:
[
0
,
∞
)
→
R
{\displaystyle \ f,g:[0,\infty )\to \mathbb {R} }
对于两个得出复数 值的多元实变函数 多重积分 :
(
f
∗
g
)
(
t
1
,
t
2
,
⋯
,
t
n
)
≜
∫
∫
⋯
∫
R
n
f
(
τ
1
,
τ
2
,
⋯
,
τ
n
)
g
(
t
1
−
τ
1
,
t
2
−
τ
2
,
⋯
,
t
n
−
τ
n
,
)
d
τ
1
d
τ
2
⋯
d
τ
n
≜
∫
R
n
f
(
τ
)
g
(
t
−
τ
)
d
n
τ
{\displaystyle {\begin{aligned}(f*g)(t_{1},t_{2},\cdots ,t_{n})&\triangleq \int \int \cdots \int _{\mathbb {R} ^{n}}f(\tau _{1},\tau _{2},\cdots ,\tau _{n})g(t_{1}-\tau _{1},t_{2}-\tau _{2},\cdots ,t_{n}-\tau _{n},)\,d\tau _{1}d\tau _{2}\cdots d\tau _{n}\\&\triangleq \int _{\mathbb {R} ^{n}}f(\tau )g(t-\tau )\,d^{n}\tau \end{aligned}}}
卷积有一个通用的工程上的符号约定[1]
f
(
t
)
∗
g
(
t
)
≜
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
d
τ
⏟
(
f
∗
g
)
(
t
)
{\displaystyle f(t)*g(t)\triangleq \underbrace {\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau } _{(f*g)(t)}}
它必须被谨慎解释以避免混淆。例如:
f
(
t
)
∗
g
(
t
−
t
0
)
{\displaystyle f(t)*g(t-t_{0})}
(
f
∗
g
)
(
t
−
t
0
)
{\displaystyle (f*g)(t-t_{0})}
f
(
t
−
t
0
)
∗
g
(
t
−
t
0
)
{\displaystyle f(t-t_{0})*g(t-t_{0})}
(
f
∗
g
)
(
t
−
2
t
0
)
{\displaystyle (f*g)(t-2t_{0})}
[2]
卷积运算的最早使用出现在达朗贝尔 于1754年出版的《宇宙体系的几个要点研究》中对泰勒定理 的推导之中[3] 西尔维斯特·拉克鲁瓦
∫
f
(
u
)
⋅
g
(
x
−
u
)
d
u
{\textstyle \int f(u)\cdot g(x-u)\,du}
[4] 皮埃尔-西蒙·拉普拉斯 、约瑟夫·傅里叶 和西梅翁·泊松 等人的著作中。这个运算以前有时叫做“Faltung”(德语中的折叠)、合成乘积、叠加积分或卡森积分[5]
“卷积”这个术语早在1903年就出现了,然而其定义在早期使用中是相当生僻的[6] [7]
如果
f
{\displaystyle f}
g
{\displaystyle g}
Lp 空间
L
1
(
R
n
)
{\displaystyle L^{1}(\mathbb {R} ^{n})}
勒贝格可积函数 ,则二者的卷积存在,并且在这种情况下
f
∗
g
{\displaystyle f*g}
[8] 托內利定理 的结论。对于在
L
1
{\displaystyle L^{1}}
f
∈
L
1
(
R
n
)
{\displaystyle f\in L^{1}(\mathbb {R} ^{n})}
g
∈
L
p
(
R
n
)
{\displaystyle g\in L^{p}(\mathbb {R} ^{n})}
1
≤
p
≤
∞
{\displaystyle 1\leq p\leq \infty }
f
∗
g
∈
L
p
(
R
n
)
{\displaystyle f*g\in L^{p}(\mathbb {R} ^{n})}
Lp 范数 间有着不等式 :
‖
f
∗
g
‖
p
≤
‖
f
‖
1
‖
g
‖
p
{\displaystyle \|{f}*g\|_{p}\leq \|f\|_{1}\|g\|_{p}}
在
p
=
1
{\displaystyle p=1}
L
1
{\displaystyle L^{1}}
巴拿赫代数 (并且如果
f
{\displaystyle f}
g
{\displaystyle g}
几乎处处 非负则两边间等式成立)。
卷积与傅里叶变换 有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,利用此一性質,能簡化傅里叶分析中的许多问题。
由卷积得到的函数
f
∗
g
{\displaystyle f*g}
f
{\displaystyle f}
g
{\displaystyle g}
g
{\displaystyle g}
光滑函数 ,
f
{\displaystyle f}
f
∗
g
{\displaystyle f*g}
f
{\displaystyle f}
f
{\displaystyle f}
f
s
{\displaystyle f_{s}}
正则化 。
函数
f
(
t
)
{\displaystyle f(t)}
g
(
t
)
{\displaystyle g(t)}
互相关
(
f
⋆
g
)
(
τ
)
{\displaystyle (f\star g)(\tau )}
f
(
−
τ
)
{\displaystyle f(-\tau )}
共轭复数
f
(
−
τ
)
¯
{\displaystyle {\overline {f(-\tau )}}}
g
(
τ
)
{\displaystyle g(\tau )}
(
f
⋆
g
)
(
τ
)
≜
∫
−
∞
∞
f
(
t
−
τ
)
¯
g
(
t
)
d
t
=
f
(
−
τ
)
¯
∗
g
(
τ
)
{\displaystyle (f\star g)(\tau )\triangleq \int _{-\infty }^{\infty }{\overline {f(t-\tau )}}g(t)\,dt={\overline {f(-\tau )}}*g(\tau )}
这里的
τ
{\displaystyle \tau }
对于單位脈衝 函数
δ
(
t
)
{\displaystyle \delta (t)}
h
(
t
)
{\displaystyle h(t)}
h
(
t
)
{\displaystyle h(t)}
h
(
t
)
{\displaystyle h(t)}
衝激響應 :
(
δ
∗
h
)
(
t
)
=
∫
−
∞
∞
δ
(
τ
)
h
(
t
−
τ
)
d
τ
=
h
(
t
)
{\displaystyle (\delta *h)(t)=\int _{-\infty }^{\infty }\delta (\tau )h(t-\tau )\,d\tau =h(t)}
在连续时间线性非时变系统 中,输出信号
y
(
t
)
{\displaystyle y(t)}
信号
x
(
t
)
{\displaystyle x(t)}
冲激响应
h
(
t
)
{\displaystyle h(t)}
[9]
y
(
t
)
=
(
x
∗
h
)
(
t
)
≜
∫
−
∞
∞
x
(
t
−
τ
)
⋅
h
(
τ
)
d
τ
=
∫
−
∞
∞
x
(
τ
)
⋅
h
(
t
−
τ
)
d
τ
{\displaystyle y(t)=(x*h)(t)\ \triangleq \ \int \limits _{-\infty }^{\infty }x(t-\tau )\cdot h(\tau )\,\mathrm {d} \tau =\int \limits _{-\infty }^{\infty }x(\tau )\cdot h(t-\tau )\,\mathrm {d} \tau }
两个独立 的随机变量
U
{\displaystyle U}
V
{\displaystyle V}
概率密度函数 ,二者之和的概率密度,是它们单独的密度函数的卷积:
f
U
+
V
(
x
)
=
∫
−
∞
∞
f
U
(
y
)
f
V
(
x
−
y
)
d
y
=
(
f
U
∗
f
V
)
(
x
)
{\displaystyle f_{U+V}(x)=\int _{-\infty }^{\infty }f_{U}(y)f_{V}(x-y)\,dy=\left(f_{U}*f_{V}\right)(x)}
已知右侧第一行图中两个函数
f
(
t
)
{\displaystyle f(t)}
g
(
t
)
{\displaystyle g(t)}
首先將兩個函數都用约束变量
τ
{\displaystyle \tau }
g
(
τ
)
{\displaystyle g(\tau )}
f
(
τ
)
{\displaystyle f(\tau )}
g
(
−
τ
)
{\displaystyle g(-\tau )}
向函数
g
(
−
τ
)
{\displaystyle g(-\tau )}
t
{\displaystyle t}
g
(
−
(
τ
−
t
)
)
=
g
(
t
−
τ
)
{\displaystyle g(-(\tau -t))=g(t-\tau )}
t
{\displaystyle t}
常数 而是自由变量 ,当
t
{\displaystyle t}
g
(
t
−
τ
)
{\displaystyle g(t-\tau )}
τ
{\displaystyle \tau }
t
{\displaystyle t}
g
(
t
−
τ
)
{\displaystyle g(t-\tau )}
g
(
−
τ
)
{\displaystyle g(-\tau )}
τ
{\displaystyle \tau }
+
∞
{\displaystyle +\infty }
t
{\displaystyle t}
t
{\displaystyle t}
g
(
t
−
τ
)
{\displaystyle g(t-\tau )}
g
(
−
τ
)
{\displaystyle g(-\tau )}
−
∞
{\displaystyle -\infty }
|
t
|
{\displaystyle |t|}
讓
t
{\displaystyle t}
−
∞
{\displaystyle -\infty }
+
∞
{\displaystyle +\infty }
t
{\displaystyle t}
f
(
τ
)
{\displaystyle f(\tau )}
权重函数
g
(
t
−
τ
)
{\displaystyle g(t-\tau )}
t
=
0
{\displaystyle t=0}
t
=
2.5
{\displaystyle t=2.5}
t
=
5.5
{\displaystyle t=5.5}
t
>
1
{\displaystyle t>1}
τ
=
0
{\displaystyle \tau =0}
g
(
t
−
τ
)
=
g
(
2.5
)
{\displaystyle g(t-\tau )=g(2.5)}
τ
=
1.5
{\displaystyle \tau =1.5}
g
(
t
−
τ
)
=
g
(
1
)
{\displaystyle g(t-\tau )=g(1)}
τ
∉
[
0
,
1.5
]
{\displaystyle \tau \notin [0,1.5]}
f
(
τ
)
g
(
t
−
τ
)
=
0
{\displaystyle f(\tau )g(t-\tau )=0}
最後得到的波形 (未包含在此圖中)就是
f
{\displaystyle f}
g
{\displaystyle g}
两个矩形 脈衝波 的捲積。其中函数
g
{\displaystyle g}
τ
=
0
{\displaystyle \tau =0}
t
{\displaystyle t}
g
(
t
−
τ
)
{\displaystyle g(t-\tau )}
t
{\displaystyle t}
τ
{\displaystyle \tau }
f
∗
g
{\displaystyle f\ast g}
t
{\displaystyle t}
矩形 脈衝波 和指數衰減 脈衝波 的捲積(後者可能出現於RC電路 中),同樣地重疊部份面積就相當於
t
{\displaystyle t}
g
{\displaystyle g}
两个
T
{\displaystyle T}
h
T
(
t
)
{\displaystyle h_{_{T}}(t)}
x
T
(
t
)
{\displaystyle x_{_{T}}(t)}
[10] [11]
∫
t
0
t
0
+
T
h
T
(
τ
)
x
T
(
t
−
τ
)
d
τ
{\displaystyle \int _{t_{0}}^{t_{0}+T}h_{_{T}}(\tau )x_{_{T}}(t-\tau )\,d\tau }
这里的
t
0
{\displaystyle t_{0}}
任何可积分函数
s
(
t
)
{\displaystyle s(t)}
s
(
t
)
{\displaystyle s(t)}
整数倍
P
{\displaystyle P}
平移 的总和 ,从而制作出具有周期
P
{\displaystyle P}
周期函数
s
P
(
t
)
{\displaystyle s_{_{P}}(t)}
周期求和
s
P
(
t
)
≜
∑
m
=
−
∞
∞
s
(
t
+
m
P
)
=
∑
m
=
−
∞
∞
s
(
t
−
m
P
)
,
m
∈
Z
{\displaystyle s_{_{P}}(t)\triangleq \sum _{m=-\infty }^{\infty }s(t+mP)=\sum _{m=-\infty }^{\infty }s(t-mP),\quad m\in \mathbb {Z} }
对于无周期函数
h
{\displaystyle h}
x
{\displaystyle x}
T
{\displaystyle T}
h
T
(
t
)
{\displaystyle h_{_{T}}(t)}
x
T
(
t
)
{\displaystyle x_{_{T}}(t)}
h
{\displaystyle h}
x
{\displaystyle x}
h
(
t
)
{\displaystyle h(t)}
x
T
(
t
)
{\displaystyle x_{_{T}}(t)}
x
(
t
)
{\displaystyle x(t)}
h
T
(
t
)
{\displaystyle h_{_{T}}(t)}
h
T
(
t
)
{\displaystyle h_{_{T}}(t)}
x
T
(
t
)
{\displaystyle x_{_{T}}(t)}
(
h
∗
x
T
)
(
t
)
≜
∫
−
∞
∞
h
(
τ
)
x
T
(
t
−
τ
)
d
τ
=
∫
t
0
t
0
+
T
h
T
(
τ
)
x
T
(
t
−
τ
)
d
τ
{\displaystyle (h*x_{_{T}})(t)\ \triangleq \ \ \int _{-\infty }^{\infty }h(\tau )x_{_{T}}(t-\tau )\,d\tau \ =\ \int _{t_{0}}^{t_{0}+T}h_{_{T}}(\tau )x_{_{T}}(t-\tau )\,d\tau }
(
h
∗
x
T
)
(
t
)
=
(
x
∗
h
T
)
(
t
)
{\displaystyle (h*x_{_{T}})(t)=(x*h_{_{T}})(t)}
圆周卷积 是周期卷积的特殊情况[11] [12]
h
{\displaystyle h}
x
{\displaystyle x}
[
0
,
T
]
{\displaystyle [0,T]}
h
∗
x
T
{\displaystyle h*x_{_{T}}}
x
T
{\displaystyle x_{_{T}}}
非负 余数 的模除 运算表达为“圆周函数”:
x
T
(
t
)
=
x
(
t
m
o
d
T
)
,
t
∈
R
{\displaystyle x_{_{T}}(t)=x(t_{\mathrm {mod} \ T}),\quad t\in \mathbb {R} }
而积分的界限可以缩简至函数
h
{\displaystyle h}
[
0
,
T
]
{\displaystyle [0,T]}
(
h
∗
x
T
)
(
t
)
=
∫
0
T
h
(
τ
)
x
(
(
t
−
τ
)
m
o
d
T
)
d
τ
{\displaystyle (h*x_{_{T}})(t)=\int _{0}^{T}h(\tau )x((t-\tau )_{\mathrm {mod} \ T})\ d\tau }
离散卷积示意图 对于定义在整數
Z
{\displaystyle \mathbb {Z} }
复数 值的函数
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
[13]
(
f
∗
g
)
[
n
]
≜
∑
m
=
−
∞
∞
f
[
m
]
g
[
n
−
m
]
=
∑
m
=
−
∞
∞
f
[
n
−
m
]
g
[
m
]
{\displaystyle (f*g)[n]\ \ \triangleq \ \sum _{m=-\infty }^{\infty }{f[m]g[n-m]}=\sum _{m=-\infty }^{\infty }f[n-m]\,g[m]}
這裡一樣把函數定義域以外的值當成零,所以可以擴展函數到所有整數上(如果本來不是的話)。两个有限序列的卷积的定义,是将这些序列扩展成在整数集合上有限支撑的函数。在这些序列是两个多项式 的系数之时,这两个多项式的普通乘积的系数,就是这两个序列的卷积。这叫做序列系数的柯西乘积 。
當
g
[
n
]
{\displaystyle g[n]}
支撐集 為有限長度的
{
−
M
,
−
M
+
1
,
…
,
M
−
1
,
M
}
{\displaystyle \{-M,-M+1,\dots ,M-1,M\}}
求和 :
(
f
∗
g
)
[
n
]
=
∑
m
=
−
M
M
f
[
n
−
m
]
g
[
m
]
{\displaystyle (f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m]}
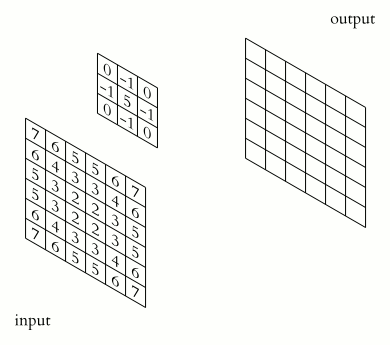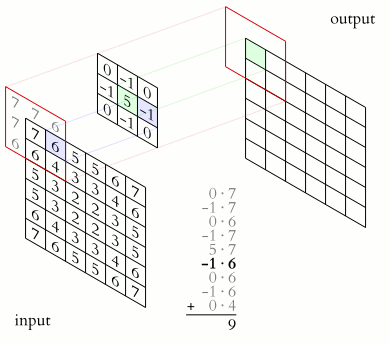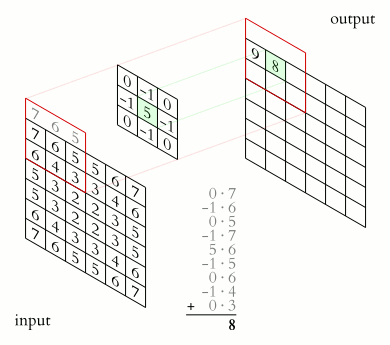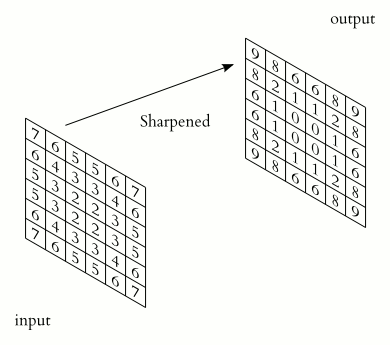
用离散二维卷积对图像 进行锐化 处理 的动画 类似于一维情况,使用星号 表示卷积,而维度体现在星号的数量上,
M
{\displaystyle M}
M
{\displaystyle M}
M
{\displaystyle M}
y
(
n
1
,
n
2
,
.
.
.
,
n
M
)
=
h
(
n
1
,
n
2
,
.
.
.
,
n
M
)
∗
⋯
M
∗
x
(
n
1
,
n
2
,
.
.
.
,
n
M
)
{\displaystyle y(n_{1},n_{2},...,n_{_{M}})=h(n_{1},n_{2},...,n_{_{M}})*{\overset {M}{\cdots }}*x(n_{1},n_{2},...,n_{_{M}})}
对于离散值的信号,这个卷积可以直接如下这样计算:
∑
k
1
=
−
∞
∞
∑
k
2
=
−
∞
∞
.
.
.
∑
k
M
=
−
∞
∞
h
(
k
1
,
k
2
,
.
.
.
,
k
M
)
x
(
n
1
−
k
1
,
n
2
−
k
2
,
.
.
.
,
n
M
−
k
M
)
{\displaystyle \sum _{k_{1}=-\infty }^{\infty }\sum _{k_{2}=-\infty }^{\infty }...\sum _{k_{_{M}}=-\infty }^{\infty }h(k_{1},k_{2},...,k_{_{M}})x(n_{1}-k_{1},n_{2}-k_{2},...,n_{_{M}}-k_{_{M}})}
结果的离散多维卷积所支撑的输出区域,基于两个输入信号所支撑的大小和区域来决定。
在两个二维信号之间的卷积的可视化 对比离散无周期卷积(左列)与离散圆周卷积(右列) 对于离散序列和一个参数
N
{\displaystyle N}
h
{\displaystyle h}
x
{\displaystyle x}
(
h
∗
x
N
)
[
n
]
≜
∑
m
=
−
∞
∞
h
[
m
]
x
N
[
n
−
m
]
⏟
∑
k
=
−
∞
∞
x
[
n
−
m
−
k
N
]
=
∑
m
=
0
N
−
1
(
∑
k
=
−
∞
∞
h
[
m
−
k
N
]
)
x
N
[
n
−
m
]
{\displaystyle (h*x_{_{N}})[n]\ \triangleq \ \sum _{m=-\infty }^{\infty }h[m]\underbrace {x_{_{N}}[n-m]} _{\sum _{k=-\infty }^{\infty }x[n-m-kN]}\ =\ \sum _{m=0}^{N-1}\left(\sum _{k=-\infty }^{\infty }{h}[m-kN]\right)x_{_{N}}[n-m]}
这个函数有周期
N
{\displaystyle N}
N
{\displaystyle N}
h
{\displaystyle h}
x
{\displaystyle x}
[
0
,
N
−
1
]
{\displaystyle [0,N-1]}
圆周卷积 :
(
h
∗
x
N
)
[
n
]
=
∑
m
=
0
N
−
1
h
[
m
]
x
N
[
n
−
m
]
=
∑
m
=
0
N
−
1
h
[
m
]
x
[
(
n
−
m
)
mod
N
]
{\displaystyle (h*x_{_{N}})[n]=\sum _{m=0}^{N-1}h[m]x_{_{N}}[n-m]=\sum _{m=0}^{N-1}h[m]x[(n-m)_{\bmod {N}}]}
离散圆周卷积可简约为矩阵乘法 ,这里的积分变换 的核函数是循环矩阵 :
[
y
0
y
1
⋮
y
N
−
1
]
=
[
h
0
h
N
−
1
⋯
h
1
h
1
h
0
⋯
h
2
⋮
⋮
⋱
⋮
h
N
−
1
h
N
−
2
⋯
h
0
]
[
x
0
x
1
⋮
x
N
−
1
]
{\displaystyle {\begin{bmatrix}y_{0}\\y_{1}\\\vdots \\y_{_{N-1}}\end{bmatrix}}={\begin{bmatrix}h_{0}&h_{_{N-1}}&\cdots &h_{1}\\h_{1}&h_{0}&\cdots &h_{2}\\\vdots &\vdots &\ddots &\vdots \\h_{_{N-1}}&h_{_{N-2}}&\cdots &h_{0}\end{bmatrix}}{\begin{bmatrix}x_{0}\\x_{1}\\\vdots \\x_{_{N-1}}\end{bmatrix}}}
圆周卷积最经常出现的快速傅里叶变换 的实现算法比如雷德演算法 之中。
各种卷积算子都满足下列性质:
交换律
f
∗
g
=
g
∗
f
{\displaystyle f*g=g*f\,}
结合律
f
∗
(
g
∗
h
)
=
(
f
∗
g
)
∗
h
{\displaystyle f*(g*h)=(f*g)*h\,}
分配律
f
∗
(
g
+
h
)
=
(
f
∗
g
)
+
(
f
∗
h
)
{\displaystyle f*(g+h)=(f*g)+(f*h)\,}
数乘结合律
a
(
f
∗
g
)
=
(
a
f
)
∗
g
=
f
∗
(
a
g
)
{\displaystyle a(f*g)=(af)*g=f*(ag)\,}
其中
a
{\displaystyle a}
实数 (或复数 )。
复数共轭
f
∗
g
¯
=
f
¯
∗
g
¯
{\displaystyle {\overline {f*g}}={\overline {f}}*{\overline {g}}}
微分有关
(
f
∗
g
)
′
=
f
′
∗
g
=
f
∗
g
′
{\displaystyle (f*g)'=f'*g=f*g'}
积分有关
如果
F
(
t
)
=
∫
−
∞
t
f
(
τ
)
d
τ
{\textstyle F(t)=\int _{-\infty }^{t}f(\tau )d\tau }
G
(
t
)
=
∫
−
∞
t
g
(
τ
)
d
τ
{\textstyle G(t)=\int _{-\infty }^{t}g(\tau )\,d\tau }
(
F
∗
g
)
(
t
)
=
(
f
∗
G
)
(
t
)
=
∫
−
∞
t
(
f
∗
g
)
(
τ
)
d
τ
{\displaystyle (F*g)(t)=(f*G)(t)=\int _{-\infty }^{t}(f*g)(\tau )\,d\tau }
如果
f
{\displaystyle f}
g
{\displaystyle g}
[14]
∫
R
n
(
f
∗
g
)
(
t
)
d
n
t
=
(
∫
R
n
f
(
t
)
d
n
t
)
(
∫
R
n
g
(
t
)
d
n
t
)
{\displaystyle \int _{\mathbb {R} ^{n}}(f*g)(t)\,d^{n}t=\left(\int _{\mathbb {R} ^{n}}f(t)\,d^{n}t\right)\left(\int _{\mathbb {R} ^{n}}g(t)\,d^{n}t\right)}
这是富比尼定理 的结果。如果
f
{\displaystyle f}
g
{\displaystyle g}
托内利定理 ,这也是成立的。
在一元函数情况下,
f
{\displaystyle f}
g
{\displaystyle g}
导数 有着:
d
d
t
(
f
∗
g
)
=
d
f
d
t
∗
g
=
f
∗
d
g
d
t
{\displaystyle {\frac {d}{dt}}(f*g)={\frac {df}{dt}}*g=f*{\frac {dg}{dt}}}
这里的
d
d
t
{\displaystyle {\frac {d}{dt}}}
微分算子 。更一般的说,在多元函数 的情况下,对偏导数 也有类似的公式:
∂
∂
t
i
(
f
∗
g
)
=
∂
f
∂
t
i
∗
g
=
f
∗
∂
g
∂
t
i
{\displaystyle {\frac {\partial }{\partial t_{i}}}(f*g)={\frac {\partial f}{\partial t_{i}}}*g=f*{\frac {\partial g}{\partial t_{i}}}}
这就有了一个特殊结论,卷积可以看作“光滑”运算:
f
{\displaystyle f}
g
{\displaystyle g}
f
{\displaystyle f}
g
{\displaystyle g}
这些恒等式成立的严格条件,为
f
{\displaystyle f}
g
{\displaystyle g}
L
1
{\displaystyle L^{1}}
Young卷积不等式
在离散情况下,差分 算子
Δ
[
f
]
(
n
)
=
f
(
n
+
1
)
−
f
(
n
)
{\displaystyle \Delta [f](n)=f(n+1)-f(n)}
Δ
(
f
∗
g
)
=
(
Δ
f
)
∗
g
=
f
∗
(
Δ
g
)
{\displaystyle \Delta (f*g)=(\Delta f)*g=f*(\Delta g)}
卷积定理 指出[15] 信号 )的卷积的傅里叶变换 ,是它们的傅里叶变换的逐点乘积 。更一般的说,在一个域(比如时域 )中的卷积等于在其他域(比如频域 )逐点 乘法。
设两个函数
g
(
x
)
{\displaystyle g(x)}
h
(
x
)
{\displaystyle h(x)}
傅里叶变换
G
(
s
)
{\displaystyle G(s)}
H
(
s
)
{\displaystyle H(s)}
G
(
s
)
≜
F
{
g
}
(
s
)
=
∫
−
∞
∞
g
(
x
)
e
−
i
2
π
s
x
d
x
,
s
∈
R
H
(
s
)
≜
F
{
h
}
(
s
)
=
∫
−
∞
∞
h
(
x
)
e
−
i
2
π
s
x
d
x
,
s
∈
R
{\displaystyle {\begin{aligned}G(s)&\triangleq {\mathcal {F}}\{g\}(s)=\int _{-\infty }^{\infty }g(x)e^{-i2\pi sx}\,dx,\quad s\in \mathbb {R} \\H(s)&\triangleq {\mathcal {F}}\{h\}(s)=\int _{-\infty }^{\infty }h(x)e^{-i2\pi sx}\,dx,\quad s\in \mathbb {R} \end{aligned}}}
这里的
F
{\displaystyle {\mathcal {F}}}
算子 指示傅里叶变换 。
卷积定理声称:
F
{
g
∗
h
}
(
s
)
=
G
(
s
)
H
(
s
)
,
s
∈
R
{\displaystyle {\mathcal {F}}\{g*h\}(s)=G(s)H(s),\quad s\in \mathbb {R} }
F
{
g
⋅
h
}
(
s
)
=
G
(
s
)
∗
H
(
s
)
,
s
∈
R
{\displaystyle {\mathcal {F}}\{g\cdot h\}(s)=G(s)*H(s),\quad s\in \mathbb {R} }
应用逆傅里叶变换
F
−
1
{\displaystyle {\mathcal {F}}^{-1}}
(
g
∗
h
)
(
s
)
=
F
−
1
{
G
⋅
H
}
,
s
∈
R
{\displaystyle (g*h)(s)={\mathcal {F}}^{-1}\{G\cdot H\},\quad s\in \mathbb {R} }
(
g
⋅
h
)
(
s
)
=
F
−
1
{
G
∗
H
}
,
s
∈
R
{\displaystyle (g\cdot h)(s)={\mathcal {F}}^{-1}\{G*H\},\quad s\in \mathbb {R} }
这里的算符
⋅
{\displaystyle \,\cdot \,}
逐点 乘法。
这一定理对拉普拉斯变换 、双边拉普拉斯变换 、Z变换 、梅林变换 和Hartley变换 调和分析 中还可以推广到在局部紧致的阿贝尔群 上定义的傅里叶变换。
对于周期为
P
{\displaystyle P}
g
P
(
x
)
{\displaystyle g_{_{P}}(x)}
h
P
(
x
)
{\displaystyle h_{_{P}}(x)}
周期求和
g
P
(
x
)
≜
∑
m
=
−
∞
∞
g
(
x
−
m
P
)
,
m
∈
Z
h
P
(
x
)
≜
∑
m
=
−
∞
∞
h
(
x
−
m
P
)
,
m
∈
Z
{\displaystyle {\begin{aligned}g_{_{P}}(x)\ &\triangleq \sum _{m=-\infty }^{\infty }g(x-mP),\quad m\in \mathbb {Z} \\h_{_{P}}(x)\ &\triangleq \sum _{m=-\infty }^{\infty }h(x-mP),\quad m\in \mathbb {Z} \end{aligned}}}
它们的傅里叶级数 系数 为:
G
[
k
]
≜
F
{
g
P
}
[
k
]
=
1
P
∫
P
g
P
(
x
)
e
−
i
2
π
k
x
/
P
d
x
,
k
∈
Z
H
[
k
]
≜
F
{
h
P
}
[
k
]
=
1
P
∫
P
h
P
(
x
)
e
−
i
2
π
k
x
/
P
d
x
,
k
∈
Z
{\displaystyle {\begin{aligned}G[k]&\triangleq {\mathcal {F}}\{g_{_{P}}\}[k]={\frac {1}{P}}\int _{P}g_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \\H[k]&\triangleq {\mathcal {F}}\{h_{_{P}}\}[k]={\frac {1}{P}}\int _{P}h_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \end{aligned}}}
这里的
F
{\displaystyle {\mathcal {F}}}
傅里叶级数 积分 。
逐点乘积
g
P
(
x
)
⋅
h
P
(
x
)
{\displaystyle g_{_{P}}(x)\cdot h_{_{P}}(x)}
P
{\displaystyle P}
F
{
g
P
⋅
h
P
}
[
k
]
=
(
G
∗
H
)
[
k
]
{\displaystyle {\mathcal {F}}\{g_{_{P}}\cdot h_{_{P}}\}[k]=(G*H)[k]}
周期卷积
(
g
P
∗
h
)
(
x
)
{\displaystyle (g_{_{P}}*h)(x)}
P
{\displaystyle P}
F
{
g
P
∗
h
}
[
k
]
=
P
⋅
G
[
k
]
H
[
k
]
{\displaystyle {\mathcal {F}}\{g_{_{P}}*h\}[k]=\ P\cdot G[k]\ H[k]}
对于作为两个连续函数采样 的序列
g
[
n
]
{\displaystyle g[n]}
h
[
n
]
{\displaystyle h[n]}
离散时间傅里叶变换
G
(
s
)
{\displaystyle G(s)}
H
(
s
)
{\displaystyle H(s)}
G
(
s
)
≜
F
{
g
}
(
s
)
=
∑
n
=
−
∞
∞
g
[
n
]
⋅
e
−
i
2
π
s
n
,
s
∈
R
H
(
s
)
≜
F
{
h
}
(
s
)
=
∑
n
=
−
∞
∞
h
[
n
]
⋅
e
−
i
2
π
s
n
,
s
∈
R
{\displaystyle {\begin{aligned}G(s)&\triangleq {\mathcal {F}}\{g\}(s)=\sum _{n=-\infty }^{\infty }g[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \\H(s)&\triangleq {\mathcal {F}}\{h\}(s)=\sum _{n=-\infty }^{\infty }h[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \end{aligned}}}
这里的
F
{\displaystyle {\mathcal {F}}}
离散时间傅里叶变换 (DTFT)。
离散卷积的卷积定理为:
F
{
g
∗
h
}
(
s
)
=
G
(
s
)
H
(
s
)
{\displaystyle {\mathcal {F}}\{g*h\}(s)=\ G(s)H(s)}
对于周期为
N
{\displaystyle N}
序列
g
N
[
n
]
{\displaystyle g_{_{N}}[n]}
h
N
[
n
]
{\displaystyle h_{_{N}}[n]}
g
N
[
n
]
≜
∑
m
=
−
∞
∞
g
[
n
−
m
N
]
,
m
,
n
∈
Z
h
N
[
n
]
≜
∑
m
=
−
∞
∞
h
[
n
−
m
N
]
,
m
,
n
∈
Z
{\displaystyle {\begin{aligned}g_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }g[n-mN],\quad m,n\in \mathbb {Z} \\h_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }h[n-mN],\quad m,n\in \mathbb {Z} \end{aligned}}}
相较于离散时间傅里叶变换
G
(
s
)
{\displaystyle G(s)}
H
(
s
)
{\displaystyle H(s)}
1
{\displaystyle 1}
1
/
N
{\displaystyle 1/N}
G
(
s
)
{\displaystyle G(s)}
H
(
s
)
{\displaystyle H(s)}
N
{\displaystyle N}
离散傅里叶变换 (DFT-1 或IDFT)的结果。
离散周期卷积
(
g
N
∗
h
)
[
n
]
{\displaystyle (g_{_{N}}*h)[n]}
N
{\displaystyle N}
F
{
g
N
∗
h
}
[
k
]
=
F
{
g
N
}
[
k
]
⏟
G
(
k
/
N
)
⋅
F
{
h
N
}
[
k
]
⏟
H
(
k
/
N
)
,
k
,
n
∈
Z
{\displaystyle {\mathcal {F}}\{g_{_{N}}*h\}[k]=\ \underbrace {{\mathcal {F}}\{g_{_{N}}\}[k]} _{G(k/N)}\cdot \underbrace {{\mathcal {F}}\{h_{_{N}}\}[k]} _{H(k/N)},\quad k,n\in \mathbb {Z} }
这里的
F
{\displaystyle {\mathcal {F}}}
N
{\displaystyle N}
离散傅里叶变换 (DFT)。
它有着推论:
(
g
N
∗
h
)
[
n
]
=
F
−
1
{
F
{
g
N
}
⋅
F
{
h
N
}
}
{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g_{_{N}}\}\cdot {\mathcal {F}}\{h_{_{N}}\}\}}
对于其非零时段小于等于
N
{\displaystyle N}
g
{\displaystyle g}
h
{\displaystyle h}
(
g
N
∗
h
)
[
n
]
=
F
−
1
{
F
{
g
}
⋅
F
{
h
}
}
{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g\}\cdot {\mathcal {F}}\{h\}\}}
卷积的概念还可以推广到数列 、测度 以及广义函数 上去。函数
f
,
g
{\displaystyle f,g}
R
n
{\displaystyle \mathbb {R} ^{n}}
可測函數 (measurable function),
f
{\displaystyle f}
g
{\displaystyle g}
f
∗
g
{\displaystyle f*g}
R
n
{\displaystyle \mathbb {R} ^{n}}
R
n
{\displaystyle \mathbb {R} ^{n}}
若G 是有某m 测度 的群 (例如豪斯多夫空间 上哈尔测度 下局部紧致 的拓扑群 ),对于G 上m -勒贝格可积 的实数 或复数 函数f 和g ,可定义它们的卷积:
(
f
∗
g
)
(
x
)
=
∫
G
f
(
y
)
g
(
x
y
−
1
)
d
m
(
y
)
{\displaystyle (f*g)(x)=\int _{G}f(y)g(xy^{-1})\,dm(y)\,}
对于这些群上定义的卷积同样可以给出诸如卷积定理等性质,但是这需要对这些群的表示理论 以及调和分析的彼得-外尔定理 。
計算卷積
f
[
n
]
∗
g
[
n
]
{\displaystyle f[n]*g[n]}
直接計算(Direct Method)
快速傅立葉轉換 (FFT)分段卷積(sectioned convolution) 方法1是直接利用定義來計算卷積,而方法2和3都是用到了FFT來快速計算卷積。也有不需要用到FFT的作法,如使用數論轉換 。
y
[
n
]
=
f
[
n
]
∗
g
[
n
]
=
∑
m
=
0
M
−
1
f
[
n
−
m
]
g
[
m
]
{\displaystyle y[n]=f[n]*g[n]=\sum _{m=0}^{M-1}f[n-m]g[m]}
若
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
M
N
{\displaystyle MN}
若
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
4
M
N
{\displaystyle 4MN}
3
M
N
{\displaystyle 3MN}
因此,使用定義直接計算卷積的複雜度為
O
(
M
N
)
{\displaystyle O(MN)}
概念:由於兩個離散信號在時域(time domain)做卷積相當於這兩個信號的離散傅立葉轉換在頻域(frequency domain)做相乘:
y
[
n
]
=
f
[
n
]
∗
g
[
n
]
↔
Y
[
f
]
=
F
[
f
]
G
[
f
]
{\displaystyle y[n]=f[n]*g[n]\leftrightarrow Y[f]=F[f]G[f]}
,可以看出在頻域的計算較簡單。
F
[
f
]
=
D
F
T
P
(
f
[
n
]
)
,
G
[
f
]
=
D
F
T
P
(
g
[
n
]
)
{\displaystyle F[f]=DFT_{P}(f[n]),G[f]=DFT_{P}(g[n])}
,於是
Y
[
f
]
=
D
F
T
P
(
f
[
n
]
)
D
F
T
P
(
g
[
n
]
)
{\displaystyle Y[f]=DFT_{P}(f[n])DFT_{P}(g[n])}
,最後再將頻域信號轉回時域,就完成了卷積的計算:
y
[
n
]
=
I
D
F
T
P
D
F
T
P
(
f
[
n
]
)
D
F
T
P
(
g
[
n
]
)
{\displaystyle y[n]=IDFT_{P}{DFT_{P}(f[n])DFT_{P}(g[n])}}
總共做了2次DFT和1次IDFT。 特別注意DFT和IDFT的點數
P
{\displaystyle P}
P
≥
M
+
N
−
1
{\displaystyle P\geq M+N-1}
由於DFT有快速演算法FFT,所以運算量為
O
(
P
log
2
P
)
{\displaystyle O(P\log _{2}P)}
假設
P
{\displaystyle P}
a
{\displaystyle a}
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
3
a
+
3
P
{\displaystyle 3a+3P}
概念:將
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
作法:先將
f
[
n
]
{\displaystyle f[n]}
L
{\displaystyle L}
L
>
M
{\displaystyle L>M}
f
[
n
]
(
n
=
0
,
1
,
.
.
.
,
N
−
1
)
→
f
1
[
n
]
,
f
2
[
n
]
,
f
3
[
n
]
,
.
.
.
,
f
S
[
n
]
(
S
=
⌈
N
L
⌉
)
{\displaystyle f[n](n=0,1,...,N-1)\to f_{1}[n],f_{2}[n],f_{3}[n],...,f_{S}[n](S=\left\lceil {\frac {N}{L}}\right\rceil )}
Section 1:
f
1
[
n
]
=
f
[
n
]
,
n
=
0
,
1
,
.
.
.
,
L
−
1
{\displaystyle f_{1}[n]=f[n],n=0,1,...,L-1}
Section 2:
f
2
[
n
]
=
f
[
n
+
L
]
,
n
=
0
,
1
,
.
.
.
,
L
−
1
{\displaystyle f_{2}[n]=f[n+L],n=0,1,...,L-1}
⋮
{\displaystyle \vdots }
Section r:
f
r
[
n
]
=
f
[
n
+
(
r
−
1
)
L
]
,
n
=
0
,
1
,
.
.
.
,
L
−
1
{\displaystyle f_{r}[n]=f[n+(r-1)L],n=0,1,...,L-1}
⋮
{\displaystyle \vdots }
Section S:
f
S
[
n
]
=
f
[
n
+
(
S
−
1
)
L
]
,
n
=
0
,
1
,
.
.
.
,
L
−
1
{\displaystyle f_{S}[n]=f[n+(S-1)L],n=0,1,...,L-1}
,
f
[
n
]
{\displaystyle f[n]}
f
[
n
]
=
∑
r
=
1
S
f
r
[
n
+
(
r
−
1
)
L
]
{\displaystyle f[n]=\sum _{r=1}^{S}f_{r}[n+(r-1)L]}
因此,
y
[
n
]
=
f
[
n
]
∗
g
[
n
]
=
∑
r
=
1
S
∑
m
=
0
M
−
1
f
r
[
n
+
(
r
−
1
)
L
−
m
]
g
[
m
]
{\displaystyle y[n]=f[n]*g[n]=\sum _{r=1}^{S}\sum _{m=0}^{M-1}f_{r}[n+(r-1)L-m]g[m]}
每一小段作卷積則是採用方法2,先將時域信號轉到頻域相乘,再轉回時域:
y
[
n
]
=
I
D
F
T
(
∑
r
=
1
S
∑
m
=
0
M
−
1
D
F
T
P
(
f
r
[
n
+
(
r
−
1
)
L
−
m
]
)
D
F
T
P
(
g
[
m
]
)
)
,
P
≥
M
+
L
−
1
{\displaystyle y[n]=IDFT(\sum _{r=1}^{S}\sum _{m=0}^{M-1}DFT_{P}(f_{r}[n+(r-1)L-m])DFT_{P}(g[m])),P\geq M+L-1}
總共只需要做
P
{\displaystyle P}
2
S
+
1
{\displaystyle 2S+1}
g
[
n
]
{\displaystyle g[n]}
假設
P
{\displaystyle P}
a
{\displaystyle a}
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
(
2
S
+
1
)
a
+
3
S
P
{\displaystyle (2S+1)a+3SP}
運算量:
N
L
3
(
L
+
M
−
1
)
[
log
2
(
L
+
M
−
1
)
+
1
]
{\displaystyle {\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}
運算複雜度:
O
(
N
)
{\displaystyle O(N)}
N
{\displaystyle N}
分為 Overlap-Add 和 Overlap-Save 兩種方法。 分段卷積: Overlap-Add
欲做
x
[
n
]
∗
h
[
n
]
{\displaystyle x[n]*h[n]}
x
[
n
]
{\displaystyle x[n]}
N
{\displaystyle N}
h
[
n
]
{\displaystyle h[n]}
M
{\displaystyle M}
Step 1: 將
x
[
n
]
{\displaystyle x[n]}
L
{\displaystyle L}
Step 2: 再每段
L
{\displaystyle L}
M
−
1
{\displaystyle M-1}
L
+
M
−
1
{\displaystyle L+M-1}
Step 3: 把
h
[
n
]
{\displaystyle h[n]}
L
−
1
{\displaystyle L-1}
L
+
M
−
1
{\displaystyle L+M-1}
h
′
[
n
]
{\displaystyle h'[n]}
Step 4: 把每個
x
[
n
]
{\displaystyle x[n]}
h
′
[
n
]
{\displaystyle h'[n]}
I
D
F
T
L
+
M
−
1
{
D
F
T
L
+
M
−
1
(
x
[
n
]
)
D
F
T
L
+
M
−
1
(
h
′
[
n
]
)
}
{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}
L
+
M
−
1
{\displaystyle L+M-1}
Step 5: 放置第
i
{\displaystyle i}
L
×
i
{\displaystyle L\times i}
i
=
0
,
1
,
.
.
.
,
⌈
N
L
⌉
−
1
{\displaystyle i=0,1,...,\lceil {\frac {N}{L}}\rceil -1}
Step 6: 會發現在每一段的後面
M
−
1
{\displaystyle M-1}
舉例來說:
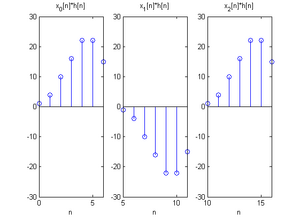
x
[
n
]
=
[
1
,
2
,
3
,
4
,
5
,
−
1
,
−
2
,
−
3
,
−
4
,
−
5
,
1
,
2
,
3
,
4
,
5
]
{\displaystyle x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]}
N
=
15
{\displaystyle N=15}
h
[
n
]
=
[
1
,
2
,
3
]
{\displaystyle h[n]=[1,2,3]}
M
=
3
{\displaystyle M=3}
令
L
=
5
{\displaystyle L=5}
令
L
=
5
{\displaystyle L=5}
x
0
[
n
]
,
x
1
[
n
]
,
x
2
[
n
]
{\displaystyle x_{0}[n],x_{1}[n],x_{2}[n]}
M
−
1
{\displaystyle M-1}
h
[
n
]
{\displaystyle h[n]}
L
+
M
−
1
{\displaystyle L+M-1}
將每一段做
I
D
F
T
L
+
M
−
1
{
D
F
T
L
+
M
−
1
(
x
[
n
]
)
D
F
T
L
+
M
−
1
(
h
′
[
n
]
)
}
{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}
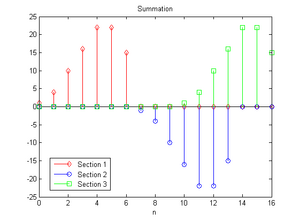
若將每小段擺在一起,可以注意到第一段的範圍是
0
∼
6
{\displaystyle 0\thicksim 6}
5
∼
11
{\displaystyle 5\thicksim 11}
10
∼
16
{\displaystyle 10\thicksim 16}
最後將三小段加在一起,並將結果和未分段的卷積做比較,上圖是分段的結果,下圖是沒有分段並利用快速卷積所算出的結果,驗證兩者運算結果相同。
分段卷積: Overlap-Save
欲做
x
[
n
]
∗
h
[
n
]
{\displaystyle x[n]*h[n]}
x
[
n
]
{\displaystyle x[n]}
N
{\displaystyle N}
h
[
n
]
{\displaystyle h[n]}
M
{\displaystyle M}
Step 1: 將
x
[
n
]
{\displaystyle x[n]}
M
−
1
{\displaystyle M-1}
Step 2: 第一段
i
=
0
{\displaystyle i=0}
x
[
n
]
{\displaystyle x[n]}
L
×
i
−
(
M
−
1
)
×
i
{\displaystyle L\times i-(M-1)\times i}
L
×
(
i
+
1
)
−
(
M
−
1
)
×
i
−
1
{\displaystyle L\times (i+1)-(M-1)\times i-1}
L
{\displaystyle L}
M
−
1
{\displaystyle M-1}
Step 3: 把
h
[
n
]
{\displaystyle h[n]}
L
−
M
{\displaystyle L-M}
L
{\displaystyle L}
h
′
[
n
]
{\displaystyle h'[n]}
Step 4: 把每個
x
[
n
]
{\displaystyle x[n]}
h
′
[
n
]
{\displaystyle h'[n]}
I
D
F
T
L
{
D
F
T
L
(
x
[
n
]
)
D
F
T
L
(
h
′
[
n
]
)
}
{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h'[n])}\}}
L
{\displaystyle L}
Step 5: 對於每個
i
{\displaystyle i}
L
−
(
M
−
1
)
{\displaystyle L-(M-1)}
Step 6: 將所有保留的點合再一起,得到最後結果
舉例來說:
x
[
n
]
=
[
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
,
11
,
12
,
13
,
14
,
15
]
{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}
N
=
15
{\displaystyle N=15}
h
[
n
]
=
[
1
,
2
,
3
]
{\displaystyle h[n]=[1,2,3]}
M
=
3
{\displaystyle M=3}
令
L
=
7
{\displaystyle L=7}
將
x
[
n
]
{\displaystyle x[n]}
M
−
1
{\displaystyle M-1}
M
−
1
{\displaystyle M-1}
再將每一段做
I
D
F
T
L
{
D
F
T
L
(
x
[
n
]
)
D
F
T
L
(
h
′
[
n
]
)
}
{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h'[n])}\}}
保留每一段末端的
L
−
(
M
−
1
)
{\displaystyle L-(M-1)}
0
∼
4
{\displaystyle 0\thicksim 4}
5
∼
9
{\displaystyle 5\thicksim 9}
10
∼
14
{\displaystyle 10\thicksim 14}
15
∼
16
{\displaystyle 15\thicksim 16}
將結果和未分段的卷積做比較,下圖是分段的結果,上圖是沒有分段並利用快速卷積所算出的結果,驗證兩者運算結果相同。
至於為什麼要把前面
M
−
1
{\displaystyle M-1}
以下以一例子來闡述:
x
[
n
]
=
[
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
]
{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10]}
L
=
10
{\displaystyle L=10}
h
[
n
]
=
[
1
,
2
,
3
,
4
,
5
]
{\displaystyle h[n]=[1,2,3,4,5]}
M
=
5
{\displaystyle M=5}
第一條藍線代表
y
{\displaystyle y}
L
{\displaystyle L}
當在做快速摺積時
I
D
F
T
L
{
D
F
T
L
(
x
[
n
]
)
D
F
T
L
(
h
′
[
n
]
)
}
{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h'[n])}\}}
L
{\displaystyle L}
而在一開始前
M
−
1
{\displaystyle M-1}
h
[
0
]
,
h
[
6
]
,
h
[
7
]
,
h
[
8
]
,
h
[
9
]
{\displaystyle h[0],h[6],h[7],h[8],h[9]}
x
[
0
]
,
x
[
6
]
,
x
[
7
]
,
x
[
8
]
,
x
[
9
]
{\displaystyle x[0],x[6],x[7],x[8],x[9]}
然而
h
[
6
]
,
h
[
7
]
,
h
[
8
]
,
h
[
9
]
{\displaystyle h[6],h[7],h[8],h[9]}
M
−
1
{\displaystyle M-1}
L
+
M
−
1
{\displaystyle L+M-1}
而今天因為在做快速摺積時長度為
L
{\displaystyle L}
M
−
1
{\displaystyle M-1}
M
−
1
{\displaystyle M-1}
為了要丟棄這
M
−
1
{\displaystyle M-1}
h
[
−
n
]
{\displaystyle h[-n]}
M
−
1
{\displaystyle M-1}
以上三種方法皆可用來計算卷積,其差別在於所需總體乘法量不同。基於運算量以及效率的考量,在計算卷積時,通常會選擇所需總體乘法量較少的方法。
以下根據
f
[
n
]
{\displaystyle f[n]}
g
[
n
]
{\displaystyle g[n]}
N
,
M
{\displaystyle N,M}
M
{\displaystyle M}
M
≪
N
{\displaystyle M\ll N}
M
≈
N
{\displaystyle M\approx N}
M
≫
N
{\displaystyle M\gg N}
N
{\displaystyle N}
基本上,以上只是粗略的分類。在實際應用時,最好還是算出三種方法所需的總乘法量,再選擇其中最有效率的方法來計算卷積。
Q1:當
N
=
2000
,
M
=
17
{\displaystyle N=2000,M=17}
Ans:
方法1:所需乘法量為
3
M
N
=
102000
{\displaystyle 3MN=102000}
方法2:
P
≥
M
+
N
−
1
=
2016
{\displaystyle P\geq M+N-1=2016}
a
=
12728
{\displaystyle a=12728}
3
(
a
+
P
)
=
44232
{\displaystyle 3(a+P)=44232}
方法3:
若切成8塊(
S
=
8
{\displaystyle S=8}
L
=
250
,
P
≥
M
+
L
−
1
=
266
{\displaystyle L=250,P\geq M+L-1=266}
P
=
288
{\displaystyle P=288}
(
2
S
+
1
)
a
+
3
S
P
=
26632
{\displaystyle (2S+1)a+3SP=26632}
但是若要找到最少的乘法量,必須依照以下步驟
(1)先找出
L
{\displaystyle L}
L
{\displaystyle L}
∂
N
L
3
(
L
+
M
−
1
)
[
log
2
(
L
+
M
−
1
)
+
1
]
∂
L
=
0
{\displaystyle {\frac {\partial {{\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}}{\partial L}}=0}
(2)由
P
≥
L
+
M
−
1
{\displaystyle P\geq L+M-1}
P
{\displaystyle P}
(3)最後由
L
=
P
+
1
−
M
{\displaystyle L=P+1-M}
L
o
p
t
{\displaystyle L_{opt}}
因此,
(1)由運算量對
L
{\displaystyle L}
L
=
85
{\displaystyle L=85}
(2)
P
≥
L
+
M
−
1
=
101
{\displaystyle P\geq L+M-1=101}
P
=
96
{\displaystyle P=96}
P
=
120
{\displaystyle P=120}
(3-1)當
P
=
96
→
a
=
280
,
L
=
P
+
1
−
M
=
80
→
S
=
25
{\displaystyle P=96\to a=280,L=P+1-M=80\to S=25}
(
2
S
+
1
)
a
+
3
S
P
=
21480
{\displaystyle (2S+1)a+3SP=21480}
(3-2)當
P
=
120
→
a
=
380
,
L
=
P
+
1
−
M
=
104
→
S
=
20
{\displaystyle P=120\to a=380,L=P+1-M=104\to S=20}
(
2
S
+
1
)
a
+
3
S
P
=
22780
{\displaystyle (2S+1)a+3SP=22780}
由此可知,切成20塊會有較好的效率,而所需總乘法量為21480。 因此,當
N
=
2000
,
M
=
17
{\displaystyle N=2000,M=17}
Q2:當
N
=
1024
,
M
=
3
{\displaystyle N=1024,M=3}
Ans:
方法1:所需乘法量為
3
M
N
=
9216
{\displaystyle 3MN=9216}
方法2:
P
≥
M
+
N
−
1
=
1026
{\displaystyle P\geq M+N-1=1026}
→
P
=
1152
,
a
=
7088
{\displaystyle \to P=1152,a=7088}
因此,所需乘法量為
3
(
a
+
P
)
=
24342
{\displaystyle 3(a+P)=24342}
方法3:
(1)由運算量對
L
{\displaystyle L}
L
=
5
{\displaystyle L=5}
(2)
P
≥
L
+
M
−
1
=
7
{\displaystyle P\geq L+M-1=7}
P
=
8
{\displaystyle P=8}
P
=
6
{\displaystyle P=6}
P
=
4
{\displaystyle P=4}
(3-1)當
P
=
8
→
a
=
4
,
L
=
P
+
1
−
M
=
6
→
S
=
171
{\displaystyle P=8\to a=4,L=P+1-M=6\to S=171}
(
2
S
+
1
)
a
+
3
S
P
=
5476
{\displaystyle (2S+1)a+3SP=5476}
(3-2)當
P
=
6
→
a
=
4
,
L
=
P
+
1
−
M
=
4
→
S
=
256
{\displaystyle P=6\to a=4,L=P+1-M=4\to S=256}
(
2
S
+
1
)
a
+
3
S
P
=
6660
{\displaystyle (2S+1)a+3SP=6660}
(3-3)當
P
=
4
→
a
=
0
,
L
=
P
+
1
−
M
=
2
→
S
=
512
{\displaystyle P=4\to a=0,L=P+1-M=2\to S=512}
(
2
S
+
1
)
a
+
3
S
P
=
6144
{\displaystyle (2S+1)a+3SP=6144}
由此可知,切成171塊會有較好的效率,而所需總乘法量為5476。 因此,當
N
=
1024
,
M
=
3
{\displaystyle N=1024,M=3}
雖然當
M
{\displaystyle M}
Q3:當
N
=
1024
,
M
=
600
{\displaystyle N=1024,M=600}
Ans:
方法1:所需乘法量為
3
M
N
=
1843200
{\displaystyle 3MN=1843200}
方法2:
P
≥
M
+
N
−
1
=
1623
{\displaystyle P\geq M+N-1=1623}
→
P
=
2016
,
a
=
12728
{\displaystyle \to P=2016,a=12728}
因此,所需乘法量為
3
(
a
+
P
)
=
44232
{\displaystyle 3(a+P)=44232}
方法3:
(1)由運算量對
L
{\displaystyle L}
L
=
1024
{\displaystyle L=1024}
(2)
P
≥
L
+
M
−
1
=
1623
{\displaystyle P\geq L+M-1=1623}
P
=
2016
{\displaystyle P=2016}
(3)當
P
=
2016
→
a
=
12728
,
L
=
P
+
1
−
M
=
1417
→
S
=
1
{\displaystyle P=2016\to a=12728,L=P+1-M=1417\to S=1}
(
2
S
+
1
)
a
+
3
S
P
=
44232
{\displaystyle (2S+1)a+3SP=44232}
由此可知,此時切成一段,就跟方法2一樣,所需總乘法量為44232。 因此,當
N
=
1024
,
M
=
600
{\displaystyle N=1024,M=600}
高斯模糊 可被用来从半色调 印刷品复原出光滑灰度数字图像。卷积在科学、工程和数学上都有很多应用:
^ Smith, Stephen W. 13.Convolution . The Scientist and Engineer's Guide to Digital Signal Processing 1. California Technical Publishing. 1997 [22 April 2016] . ISBN 0-9660176-3-3存档 于2023-06-26). ^ Irwin, J. David . 4.3. The Industrial Electronics Handbook 1. Boca Raton, FL: CRC Press. 1997: 75 . ISBN 0-8493-8343-9 ^ Dominguez-Torres, p 2
^ on page 505 of his book entitled Treatise on differences and series , which is the last of 3 volumes of the encyclopedic series: Traité du calcul différentiel et du calcul intégral , Chez Courcier, Paris, 1797–1800. Dominguez-Torres, p 4
^
R. N. Bracewell, Early work on imaging theory in radio astronomy , W. T. Sullivan (编), The Early Years of Radio Astronomy: Reflections Fifty Years After Jansky's Discovery, Cambridge University Press: 172, 2005, ISBN 978-0-521-61602-7
^
John Hilton Grace and Alfred Young, The algebra of invariants , Cambridge University Press: 40, 1903
^
Leonard Eugene Dickson, Algebraic invariants , J. Wiley: 85, 1914
^ (Stein & Weiss 1971 ,Theorem 1.3)
^ Crutchfield, Steve, The Joy of Convolution , Johns Hopkins University, October 12, 2010 [November 21, 2010] , (原始内容存档 于2013-09-11) ^
Jeruchim, Michel C.; Balaban, Philip; Shanmugan, K. Sam. Simulation of Communication Systems: Modeling, Methodology and Techniques 2nd. New York: Kluwer Academic Publishers. October 2000: 73–74. ISBN 0-30-646267-2
^ 11.0 11.1
Udayashankara, V. Real Time Digital Signal Processing. India: Prentice-Hall. June 2010: 189. ISBN 978-8-12-034049-7
^ Priemer, Roland. Introductory Signal Processing . Advanced Series in Electrical and Computer Engineering 6 . Teaneck,N.J.: World Scientific Pub Co Inc. July 1991: 286–289 [2023-10-26 ] . ISBN 9971-50-919-9存档 于2023-10-11). ^ Damelin & Miller 2011 ,第219頁^ Weisstein, Eric W. Convolution . mathworld.wolfram.com. [2021-09-22 ] . (原始内容存档 于2002-01-14) (英语) . ^ Weisstein, Eric W. From MathWorld--A Wolfram Web Resource . [2023-10-23 ] . (原始内容存档 于2000-07-11). ^ Zhang, Yingjie; Soon, Hong Geok; Ye, Dongsen; Fuh, Jerry Ying Hsi; Zhu, Kunpeng. Powder-Bed Fusion Process Monitoring by Machine Vision With Hybrid Convolutional Neural Networks . IEEE Transactions on Industrial Informatics. September 2020, 16 (9): 5769–5779 [2023-10-24 ] . ISSN 1941-0050 S2CID 213010088 doi:10.1109/TII.2019.2956078 存档 于2023-07-31). ^ Chervyakov, N.I.; Lyakhov, P.A.; Deryabin, M.A.; Nagornov, N.N.; Valueva, M.V.; Valuev, G.V. Residue Number System-Based Solution for Reducing the Hardware Cost of a Convolutional Neural Network . Neurocomputing. September 2020, 407 : 439–453 [2023-10-24 ] . S2CID 219470398 doi:10.1016/j.neucom.2020.04.018 存档 于2023-06-29) (英语) . Convolutional neural networks represent deep learning architectures that are currently used in a wide range of applications, including computer vision, speech recognition, time series analysis in finance, and many others. ^ Atlas, Homma, and Marks. An Artificial Neural Network for Spatio-Temporal Bipolar Patterns: Application to Phoneme Classification (PDF) . Neural Information Processing Systems (NIPS 1987). (原始内容存档 (PDF) 于2021-04-14).
Bracewell, R., The Fourier Transform and Its Applications 2nd, McGraw–Hill, 1986, ISBN 0-07-116043-4 Damelin, S.; Miller, W., The Mathematics of Signal Processing, Cambridge University Press, 2011, ISBN 978-1107601048 Diggle, P. J., A kernel method for smoothing point process data, Journal of the Royal Statistical Society, Series C, 1985, 34 (2): 138–147, JSTOR 2347366 S2CID 116746157 doi:10.2307/2347366 Dominguez-Torres, Alejandro (Nov 2, 2010). "Origin and history of convolution". 41 pgs. http://www.slideshare.net/Alexdfar/origin-adn-history-of-convolution (页面存档备份 ,存于互联网档案馆 ). Cranfield, Bedford MK43 OAL, UK. Retrieved Mar 13, 2013.
Ghasemi, S. Hooman; Nowak, Andrzej S., Reliability Index for Non-normal Distributions of Limit State Functions, Structural Engineering and Mechanics, 2017, 62 (3): 365–372, doi:10.12989/sem.2017.62.3.365 Grinshpan, A. Z., An inequality for multiple convolutions with respect to Dirichlet probability measure, Advances in Applied Mathematics, 2017, 82 (1): 102–119, doi:10.1016/j.aam.2016.08.001 Hewitt, Edwin; Ross, Kenneth A., Abstract harmonic analysis. Vol. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 115 2nd, Berlin, New York: Springer-Verlag , 1979, ISBN 978-3-540-09434-0MR 0551496 Hewitt, Edwin; Ross, Kenneth A., Abstract harmonic analysis. Vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag , 1970, MR 0262773 Hörmander, L. , The analysis of linear partial differential operators I, Grundl. Math. Wissenschaft. 256 , Springer, 1983, ISBN 3-540-12104-8MR 0717035 doi:10.1007/978-3-642-96750-4 Kassel, Christian, Quantum groups 155 , Berlin, New York: Springer-Verlag , 1995, ISBN 978-0-387-94370-1MR 1321145 doi:10.1007/978-1-4612-0783-2 Knuth, Donald , Seminumerical Algorithms 3rd., Reading, Massachusetts: Addison–Wesley, 1997, ISBN 0-201-89684-2 Template:Narici Beckenstein Topological Vector Spaces Reed, Michael; Simon, Barry , Methods of modern mathematical physics. II. Fourier analysis, self-adjointness, New York-London: Academic Press Harcourt Brace Jovanovich, Publishers: xv+361, 1975, ISBN 0-12-585002-6MR 0493420 Rudin, Walter , Fourier analysis on groups, Interscience Tracts in Pure and Applied Mathematics 12 , New York–London: Interscience Publishers, 1962, ISBN 0-471-52364-XMR 0152834 Template:Schaefer Wolff Topological Vector Spaces Stein, Elias ; Weiss, Guido, Introduction to Fourier Analysis on Euclidean Spaces ISBN 0-691-08078-X Sobolev, V.I., Convolution of functions , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 Strichartz, R., A Guide to Distribution Theory and Fourier Transforms, CRC Press, 1994, ISBN 0-8493-8273-4 Titchmarsh, E , Introduction to the theory of Fourier integrals 2nd, New York, N.Y.: Chelsea Pub. Co., 19481986, ISBN 978-0-8284-0324-5 Template:Trèves François Topological vector spaces, distributions and kernels Uludag, A. M. , On possible deterioration of smoothness under the operation of convolution, J. Math. Anal. Appl., 1998, 227 (2): 335–358, doi:10.1006/jmaa.1998.6091 von zur Gathen, J.; Gerhard, J ., Modern Computer Algebra, Cambridge University Press, 2003, ISBN 0-521-82646-2 Oppenheim, Alan V. ; Schafer, Ronald W. ; Buck, John R. Discrete-time signal processing 548 , 571. ISBN 0-13-754920-2 McGillem, Clare D.; Cooper, George R. Continuous and Discrete Signal and System Analysis 2. Holt, Rinehart and Winston. 1984. ISBN 0-03-061703-0 可微分计算
概论 概念 应用 硬件 软件库 实现
人物 组织 架构








 , Graduate Texts in Mathematics 155, Berlin, New York: Springer-Verlag, 1995, ISBN 978-0-387-94370-1, MR 1321145, doi:10.1007/978-1-4612-0783-2.
, Graduate Texts in Mathematics 155, Berlin, New York: Springer-Verlag, 1995, ISBN 978-0-387-94370-1, MR 1321145, doi:10.1007/978-1-4612-0783-2. , Princeton University Press, 1971, ISBN 0-691-08078-X.
, Princeton University Press, 1971, ISBN 0-691-08078-X.
 2nd. Upper Saddle River,N.J.: Prentice Hall. 1999: 548, 571. ISBN 0-13-754920-2.
2nd. Upper Saddle River,N.J.: Prentice Hall. 1999: 548, 571. ISBN 0-13-754920-2.










![{\displaystyle [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52088d5605716e18068a460dec118214954a68e9)


















































![{\displaystyle \tau \notin [0,1.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838205ce42d577093b941bc0a0fe5bcfef0b8f9c)

















![{\displaystyle [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)





![{\displaystyle f[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b176b3dbcced447341ad5ab70001ef0e3231062e)
![{\displaystyle g[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5e1d771a2385e9aeb71838a40425bb07c89525)
![{\displaystyle (f*g)[n]\ \ \triangleq \ \sum _{m=-\infty }^{\infty }{f[m]g[n-m]}=\sum _{m=-\infty }^{\infty }f[n-m]\,g[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bd9a55083d6a0d0aa8bda67d179ebc0c7970166)

![{\displaystyle (f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0a31f12e6771e6a8b1868f15214e43c8714c1d9)





![{\displaystyle (h*x_{_{N}})[n]\ \triangleq \ \sum _{m=-\infty }^{\infty }h[m]\underbrace {x_{_{N}}[n-m]} _{\sum _{k=-\infty }^{\infty }x[n-m-kN]}\ =\ \sum _{m=0}^{N-1}\left(\sum _{k=-\infty }^{\infty }{h}[m-kN]\right)x_{_{N}}[n-m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14cb0408cb58e39c596cab8ee9f1f63cb6e2fa3d)
![{\displaystyle [0,N-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d4099dcd12fea62ad089a8d26d2a14c54fc88f5)
![{\displaystyle (h*x_{_{N}})[n]=\sum _{m=0}^{N-1}h[m]x_{_{N}}[n-m]=\sum _{m=0}^{N-1}h[m]x[(n-m)_{\bmod {N}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac37f1cfe50298bfdefdcd870a5627ef30db1cee)















=f(n+1)-f(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10ef9708b32ccda9a3be9ff9c1f8865c4107cf59)
















![{\displaystyle {\begin{aligned}G[k]&\triangleq {\mathcal {F}}\{g_{_{P}}\}[k]={\frac {1}{P}}\int _{P}g_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \\H[k]&\triangleq {\mathcal {F}}\{h_{_{P}}\}[k]={\frac {1}{P}}\int _{P}h_{_{P}}(x)e^{-i2\pi kx/P}\,dx,\quad k\in \mathbb {Z} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff5ff5748d540ed77192958f5ec50cbe83ff9b2)

![{\displaystyle {\mathcal {F}}\{g_{_{P}}\cdot h_{_{P}}\}[k]=(G*H)[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec23600fe822e18dc005e7025b45caeb30a17f48)

![{\displaystyle {\mathcal {F}}\{g_{_{P}}*h\}[k]=\ P\cdot G[k]\ H[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d08db60e83b8282a9c6351dc2b556632ad6c336)
![{\displaystyle h[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89981bbbb05ffd469eeadb828c18359965985e46)
![{\displaystyle {\begin{aligned}G(s)&\triangleq {\mathcal {F}}\{g\}(s)=\sum _{n=-\infty }^{\infty }g[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \\H(s)&\triangleq {\mathcal {F}}\{h\}(s)=\sum _{n=-\infty }^{\infty }h[n]\cdot e^{-i2\pi sn}\;,\quad s\in \mathbb {R} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0173c3574eda0d0a0ab15d8aef57be616c6efd03)

![{\displaystyle g_{_{N}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30368575be97a3a4a9213a5bace7faff1a4a6371)
![{\displaystyle h_{_{N}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50abe51c291125077df860525b4c6c1c8d767595)
![{\displaystyle {\begin{aligned}g_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }g[n-mN],\quad m,n\in \mathbb {Z} \\h_{_{N}}[n]\ &\triangleq \sum _{m=-\infty }^{\infty }h[n-mN],\quad m,n\in \mathbb {Z} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a06f5589438df8b4574b428b5869c5178b9d2e7)


![{\displaystyle (g_{_{N}}*h)[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f3e5554f1c3fe2b5f2edeff4e779ccedb445a6)
![{\displaystyle {\mathcal {F}}\{g_{_{N}}*h\}[k]=\ \underbrace {{\mathcal {F}}\{g_{_{N}}\}[k]} _{G(k/N)}\cdot \underbrace {{\mathcal {F}}\{h_{_{N}}\}[k]} _{H(k/N)},\quad k,n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/88f84f790337809a2e0ba2a745b25083a4f3129c)
![{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g_{_{N}}\}\cdot {\mathcal {F}}\{h_{_{N}}\}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab487693fbf66da441eb710125e5ceff2194398e)
![{\displaystyle (g_{_{N}}*h)[n]=\ {\mathcal {F}}^{-1}\{{\mathcal {F}}\{g\}\cdot {\mathcal {F}}\{h\}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0defba14a548128651067acefb5121ba77e020c)



![{\displaystyle f[n]*g[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53f78eb841159a85c00fe9a4331825a77341e67c)
![{\displaystyle y[n]=f[n]*g[n]=\sum _{m=0}^{M-1}f[n-m]g[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1081139aae46ebd7421e11ec20351dc12688cedd)




![{\displaystyle y[n]=f[n]*g[n]\leftrightarrow Y[f]=F[f]G[f]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27f83ca717dff1b21da43e56127c50874843b8b0)
![{\displaystyle F[f]=DFT_{P}(f[n]),G[f]=DFT_{P}(g[n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af332366ed1070784c006329adcd40833e64c44d)
![{\displaystyle Y[f]=DFT_{P}(f[n])DFT_{P}(g[n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ec9e3130dcd720d4d6b1930bd492f29fee0faf)
![{\displaystyle y[n]=IDFT_{P}{DFT_{P}(f[n])DFT_{P}(g[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc12d1e8c9712ca85bf040d7e8573842c545588)





\to f_{1}[n],f_{2}[n],f_{3}[n],...,f_{S}[n](S=\left\lceil {\frac {N}{L}}\right\rceil )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b2758eba65ad177619e0d9198cc913abf649b9a)
![{\displaystyle f_{1}[n]=f[n],n=0,1,...,L-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22401ad12747eb80e3ec79d0c5b189b3c186d912)
![{\displaystyle f_{2}[n]=f[n+L],n=0,1,...,L-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccb4f0b33490a5fc67f57cb6d353087f35c3db5d)

![{\displaystyle f_{r}[n]=f[n+(r-1)L],n=0,1,...,L-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0d987ef3bab08edc0d97642435c8f97a1383304)
![{\displaystyle f_{S}[n]=f[n+(S-1)L],n=0,1,...,L-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30b353213c930583b0b65c5598ea334fdfee777)
![{\displaystyle f[n]=\sum _{r=1}^{S}f_{r}[n+(r-1)L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ad8dbc7f1039ba3824c87225b58895e27a85453)
![{\displaystyle y[n]=f[n]*g[n]=\sum _{r=1}^{S}\sum _{m=0}^{M-1}f_{r}[n+(r-1)L-m]g[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15254f6bff4b4db4f6899f0bb3e450f75e3625d)
![{\displaystyle y[n]=IDFT(\sum _{r=1}^{S}\sum _{m=0}^{M-1}DFT_{P}(f_{r}[n+(r-1)L-m])DFT_{P}(g[m])),P\geq M+L-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3c1ccb338a07511f8c82bbe1478beb62fafdea6)


![{\displaystyle {\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4b5d72adc35b450cfcc40c0d13720fa6d6bd070)

![{\displaystyle x[n]*h[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c97358d336f2e21de7913bc46fac6477eef3bc6)
![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)



![{\displaystyle h'[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7af9a0c1d0c9753adba0e2e13fc2c45e8d5698f7)
![{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h'[n])}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71884e63653a1501f77c376b182141bd9d8e86ce)



![{\displaystyle x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98580fd364a838db6ecc3c27068105c31f81d9a9)

![{\displaystyle h[n]=[1,2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67fdc55efaef23389bacd0b58cf59865377f46f4)


![x[n]和h[n]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/fc/Data_overlap_add.png/300px-Data_overlap_add.png)
![{\displaystyle x_{0}[n],x_{1}[n],x_{2}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d11383cb60875adb6faaedbf729e5956982bff0)
![分段x[n]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/30/Seperate_x_overlap_add.png/300px-Seperate_x_overlap_add.png)








![{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h'[n])}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c639c720d3a6a4922220ac66a9c31d6e8eb7987)

![{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54af19067aacc4ba29d8c5a4e661d92c3f2ab24)

![x[n]和h[n]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9e/Data_overlap_save.png/300px-Data_overlap_save.png)
![分段x[n]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b2/Seperate_x_overlap_save.png/300px-Seperate_x_overlap_save.png)







![{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/197c03fad73159099a753aa21015d7a410c619ba)

![{\displaystyle h[n]=[1,2,3,4,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01382de68d6838f4a938ab33a5ad465fa1ae6d0f)


![x[n]和h[n]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/25/Original_ov_extra.png/300px-Original_ov_extra.png)
![{\displaystyle h[0],h[6],h[7],h[8],h[9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c2e1f7ce57e74223a3049d5d803bd8af91b8019)
![{\displaystyle x[0],x[6],x[7],x[8],x[9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f004d095726b6a642d26dd6dc4bef9660ec8c17)
![{\displaystyle h[6],h[7],h[8],h[9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ccee59494bedbceae16aa4bce150fbcef8b2cf1)

![{\displaystyle h[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2160e2740fe612954bc0c6d78203d595d29076e3)














![{\displaystyle {\frac {\partial {{\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}}{\partial L}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5212be896bcbc7febbe5e992d9650c2b0ea09c6a)


































