十二平均律

十二平均律（英語：Equal temperament），又稱十二等程律，音樂律式的一種，也是當今最主流的律式。將一個八度平均分成十二等份，每等分稱為半音，音高八度音指的是頻率乘上二倍。八度音的頻率分為十二等分，即是分為十二項的等比數列，也就是每個音的頻率為前一個音的2的12次方根倍：

其近似值約為

\,{\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx \,

1.0594630943593

倍。

歷史[編輯]

公元400年左右，中國南朝數學家何承天提出世界歷史上最早有記載的十二平均律數列 900 849 802 758 715 677 638 601 570 536 509.5 479 450（原文：……黃鐘長九寸，太簇長八寸二厘，林鐘長六寸一厘，應鐘長四寸七分九厘強）^[1]。

意大利的物理學家伽利略·伽利萊的父親溫琴佐·伽利萊（英語：Vincenzo Galilei）曾試圖解決十二平均率問題，但他用的倍率是18:17，而不是 ${\sqrt[{12}]{2}}$ ，因此自乘12次後只得1.98556，不是2，他的系統只可算近似十二音階平均律^[2]。

1605年荷蘭數學家西蒙·斯特芬在一篇未完成的手稿「Van de Spiegheling der singconst」^[3]提出用 ${\sqrt[{12}]{1/2}}$ 計算十二平均律，但因計算精度不夠，他算出的弦長數字，有些偏離正確數字一至二單位之多^[4]。

西蒙·斯特芬的弦長表^[5]：

音	弦 10000	比率	正確的弦長
半音	9438	1.0595465	9438.7
全音	8909	1.0593781
1.5 音	8404	1.0600904	8409
2 倍全音	7936	1.0594758	7937
2.5 音	7491	1.0594046	7491.5
3 音	7071	1.0593975	7071.1
3.5 音	6674	1.0594845	6674.2
4 音	6298	1.0597014	6299
4.5 音	5944	1.0595558	5946
5 音	5611	1.0593477	5612.3
5.5 音	5296	1.0594788	5297.2
八度		1.0592000

西蒙·斯特芬的頻率比，每音一率，且各不相同，這是不正確的^[6]。

朱載堉發明十二平均律[編輯]

中國明代音樂家朱載堉於萬曆十二年（1584年）首次提出「新法密率」（見《律呂精義》、《樂律全書》），推算出以比率 ${\sqrt[{12}]{2}}$ 將八度音等分為十二等分的算法，並製造出十二平均律律管及律準，是世界上最早的十二平均律樂器。他用九九八十一位算盤計算出來準確到25位數字新法密率為：

律名	比率
正黃鐘	1.000000000000000000000000
倍應鍾	1.059463094359295264561825
倍無射	1.122462048309372981433533
倍南呂	1.189207115002721066717500
倍夷則	1.259921049894873164767211
倍林鍾	1.334839854170034364830832
倍蕤賓	1.414213562373095048801689
倍仲呂	1.498307076876681498799281
倍姑洗	1.587401051968199474751706
倍夾鍾	1.681792830507429086062251
倍太蔟	1.781797436280678609480452
倍大呂	1.887748625363386993283826
倍黃鐘	2.000000000000000000000000

朱載堉新法密率

朱載堉首創十二平均律樂器[編輯]

朱載堉為了驗證所創的十二平均律理論，計算出所需的長度和律管內徑，特選用上等竹子，按數據截取所需的長度，按數據鏇出內徑，分別創製世界上最早的十二平均律律管36根，分別為新法密率倍率管12根、正律管12根和半律管12根^[7]。選上好竹子製造，金門竹、班竹或紫竹都可，而當時朱載堉採用的是江南出產的筆管竹。

倍率黃鐘管的內逕取為五寸，下一根竹管的內徑為上根竹管的直徑除以 ${\sqrt[{24}]{2}}$ ：

樂器尺寸[編輯]

律數	律名	長度	內徑
1 倍律	黃鐘	2.0000 尺	0.500 尺
2 倍律	大呂	1.8877 尺	0.485 尺
3 倍律	太蔟	1.7818 尺	0.471 尺
4 倍律	夾鍾	1.6818 尺	0.458 尺
5 倍律	姑洗	1.5874 尺	0.445 尺
6 倍律	仲呂	1.4983 尺	0.432 尺
7 倍律	蕤賓	1.4142 尺	0.420 尺
8 倍律	林鍾	1.3348 尺	0.408 尺
9 倍律	夷則	1.2599 尺	0.396 尺
10 倍律	南呂	1.1892 尺	0.385 尺
11 倍律	無射	1.1224 尺	0.374 尺
12 倍律	應鍾	1.0594 尺	0.363 尺
1 正律	黃鐘	1.0000 尺	0.353 尺
2 正律	大呂	0.9439 尺	0.343 尺
3 正律	太蔟	0.8909 尺	0.333 尺
4 正律	夾鍾	0.8409 尺	0.324 尺
5 正律	姑洗	0.7937 尺	0.314 尺
6 正律	仲呂	0.7491 尺	0.306 尺
7 正律	蕤賓	0.7071 尺	0.297 尺
8 正律	林鍾	0.6674 尺	0.288 尺
9 正律	夷則	0.6299 尺	0.280 尺
10 正律	南呂	0.5946 尺	0.272 尺
11 正律	無射	0.5612 尺	0.264 尺
12 正律	應鍾	0.5297 尺	0.257 尺
1 半律	黃鐘	0.5000 尺	0.250 尺
2 半律	大呂	0.4719 尺	0.242 尺
3 半律	太蔟	0.4454 尺	0.235 尺
4 半律	夾鍾	0.4204 尺	0.229 尺
5 半律	姑洗	0.3968 尺	0.222 尺
6 半律	仲呂	0.3745 尺	0.216 尺
7 半律	蕤賓	0.3535 尺	0.210 尺
8 半律	林鍾	0.3337 尺	0.204 尺
9 半律	夷則	0.3150 尺	0.198 尺
10 半律	南呂	0.2973 尺	0.192 尺
11 半律	無射	0.2806 尺	0.187 尺
12 半律	應鍾	0.2648 尺	0.181 尺

倍率黃鐘管的內逕取為五寸，下一根竹管的內徑為上根竹管的直徑除以 ${\sqrt[{24}]{2}}$ 。

十二平均律准[編輯]

朱載堉依他對十二平均律所發明的新法密率理論，創製一種律准。用桐木製作，琴身厚四分，張琴弦12根，琴底藏一根黃鐘律管，用來定黃鐘^[8]。

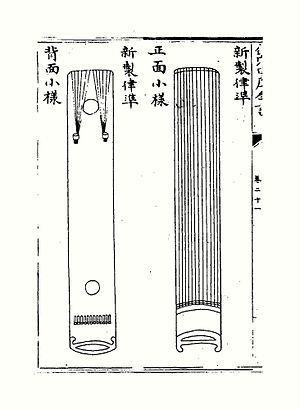
按第 1 弦為黃鐘與本弦散聲應
按第 2 弦為大呂與本弦散聲應
按第 3 弦為太蔟與本弦散聲應
按第 4 弦為夾鍾與本弦散聲應
按第 5 弦為姑洗與本弦散聲應
按第 6 弦為仲呂與本弦散聲應
按第 7 弦為蕤賓與本弦散聲應
按第 8 弦為林鍾與本弦散聲應
按第 9 弦為夷則與本弦散聲應
按第 10 弦為南呂與本弦散聲應
按第 11 弦為無射與本弦散聲應
按第 12 弦為應鍾與本弦散聲應

十二平均律准

十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准
十二平均律准

歐洲的十二平均律[編輯]

16世紀末葉中外交通方興未艾，1580年開始，明朝廣東承宣布政使司每兩年在廣州舉辦一次為時數周的交易會，屆時東西商人和傳教士會交流貨物和思想；^[9]朱載堉刊行十二平均律學說之時，正值耶穌會意大利傳教士利馬竇來華之時，利馬竇在其私人日記里提到朱載堉的曆法新理論，利馬竇本人又是精通天文學和數學，很可能知道朱載堉用 ${\sqrt[{12}]{2}}$ 來解決春分與夏至三個月之間的比率：無獨有偶，利馬竇還是法國位居高位的科學家馬蘭·梅森（Pere Marin Mersenne）的朋友，他們有共同的學術興趣，因此卓仁祥認為，在他們交往過程中，利馬竇將朱載堉獲得的 ${\sqrt[{12}]{2}}$ =1.059463094359295264561825 傳達給梅森。1638年梅森出版《和諧音概論（英語：Harmonie universelle）》，書中在西方世界第一次出現1.059463 這個數字，在此之前西方無人知道這個數字^[2]。

十九世紀德國物理學家赫爾曼·馮·亥姆霍茲在所著的論音感一書中寫道：「中國有一位王子名叫載堉，力排眾議，創導七聲音階。而將八度分成十二個半音的方法，也是這個富有天才和智巧的國家發明的」^[10]。1890年布魯塞爾皇家音樂博物館館長 Victor Charles Mahillon 按朱載堉十二平均律律管數據，複製了一套律管，經過測試之後，他寫道：「關於樂管的管徑，我們毫無所知，中國人比我們知道的多得多。我們按王子載堉的數據複製了一套律管，測試結果表明他的理論的準確性」^[11]。

十二平均律流行世界[編輯]

德國作曲家巴赫於1722年發表的《平均律鍵盤曲集》(Das Wohltemperierten Klavier，中文意思是「完美調音的鍵盤樂器」)，雖然現代中文翻譯為「平均律」，但可能並不是為使用十二平均律的鍵盤樂器而著。十二平均律的德文是Gleichschwebende Temperatur，而不是Wohltemprierte。平均律的英文是Equal Temperament，Temperament是Temper（調律）的動詞，因為百餘年來歐美各國的調律都採十二平均律，故現在習慣以Temperament表示十二平均律。

James Murray Barbour (1897, 3, 31 - 1970, 1, 04) 研究「調律技術演進史」，認為1842年由英國樂器製造廠Broadwood找到十二平均律的調律法，十二平均律才能普及。^[12] 巴赫的鍵盤樂器則是使用他的學生，音樂理論家Johann Philipp Kirnberger（英語：Johann Kirnberger）綜合中庸全音律與五度相生律的原理，所發明的調律法。

歷史上各種十二平均律的音分[編輯]

年份	人名	比率	音分
400	何承天	1.060070671	101.0
1580	伽利略·文森佐	18:17	99.0
1581	朱載堉	1.059463094	100.0
1585	西蒙·斯特芬	1.059546514	100.1
1630	馬蘭·梅森	1.059322034	99.8
1630	Johann Faulhaber	1.059490385	100.0

朱載堉顯然是歷史上最先獲得準確的100音分半音十二平均律的人；半世紀之後德國數學家Johann Faulhaber也獲得了準確的100音分。

十二平均律表[編輯]

將主音設為a1(440Hz)，來計算所有音的頻率，結果如下 （為計算過程更清晰，分數不進行約分）：

音程名稱	間隔半音數	十二平均律的倍數	頻率
純一度(A¹)	0	$2^{0}=1\,$	$440\times 1=440\,$
增一度/小二度(A♯¹/B♭¹)	1	${\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.0594630943592952645618252949463$	$440\times 2^{\frac {1}{12}}\approx 466.1637615180899164072031297762$
大二度(B¹)	2	${\sqrt[{6}]{2}}=2^{\frac {2}{12}}\approx 1.1224620483093729814335330496792$	$440\times 2^{\frac {2}{12}}\approx 493.8833012561241118307545418586$
小三度(C)	3	${\sqrt[{4}]{2}}=2^{\frac {3}{12}}\approx 1.1892071150027210667174999705605$	$440\times 2^{\frac {3}{12}}\approx 523.2511306011972693556999870466$
大三度(C♯)	4	${\sqrt[{3}]{2}}=2^{\frac {4}{12}}\approx 1.2599210498948731647672106072782$	$440\times 2^{\frac {4}{12}}\approx 554.3652619537441924975726672023$
純四度(D)	5	${\sqrt[{12}]{32}}=2^{\frac {5}{12}}\approx 1.3348398541700343648308318811845$	$440\times 2^{\frac {5}{12}}\approx 587.3295358348151205255660277209$
增四度/減五度(D#/E♭)	6	${\sqrt {2}}=2^{\frac {6}{12}}\approx 1.4142135623730950488016887242097$	$440\times 2^{\frac {6}{12}}\approx 622.2539674441618214727430386522$
純五度(E)	7	${\sqrt[{12}]{128}}=2^{\frac {7}{12}}\approx 1.4983070768766814987992807320298$	$440\times 2^{\frac {7}{12}}\approx 659.2551138257398594716835220930$
小六度(F)	8	${\sqrt[{3}]{4}}=2^{\frac {8}{12}}\approx 1.5874010519681994747517056392723$	$440\times 2^{\frac {8}{12}}\approx 698.4564628660077688907504812795$
大六度(F#)	9	${\sqrt[{4}]{8}}=2^{\frac {9}{12}}\approx 1.6817928305074290860622509524664$	$440\times 2^{\frac {9}{12}}\approx 739.9888454232687978673904190852$
小七度(G)	10	${\sqrt[{6}]{32}}=2^{\frac {10}{12}}\approx 1.781797436280678609480452411181$	$440\times 2^{\frac {10}{12}}\approx 783.9908719634985881713990609195$
大七度(G#)	11	${\sqrt[{12}]{2048}}=2^{\frac {11}{12}}\approx 1.8877486253633869932838263133351$	$440\times 2^{\frac {11}{12}}\approx 830.6093951598902770448835778670$
純八度(A)	12	$2^{1}=2\,$	$440\times 2=880\,$

其中 $\,{\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx \,$ $1.0594630943593$

\approx {\frac {18}{17}}=1.05882

99 音分

\approx {\frac {107}{101}}=1.05941

99.9 音分

\approx {\frac {11011}{10393}}=1.05946310

100 音分

參考文獻[編輯]

引用[編輯]

^ J. Murray Barbour Tuning and Temperament p55-56, Michigan State University Press 1951
^ ^2.0 ^2.1 美國北德克薩斯大學音樂學院教授卓仁祥. 《從文化史角度看十二平均律的發現》. 星海音樂學院學報. 2010年, (2期) [2019-11-12]. （原始內容存檔於2020-02-18）.
^ Simon Stevin Van de Spiegheling der singconst （頁面存檔備份，存於互聯網檔案館） 2009-6-30
^ Thomas S. Christensen, The Cambridge history of western music theory p205, Cambridge Univerity Press
^ 卓仁祥：《東西方文化視野中的朱載堉及其學術成就》，第十章，2009年，中央音樂學院出版社，151頁。ISBN 978-7-81096-325-1
^ 卓仁祥：《東西方文化視野中的朱載堉及其學術成就》，第十章，2009年，中央音樂學院出版社，152頁，ISBN 978-7-81096-325-1
^ 朱載堉維基文庫中的相關文獻：《樂律全書》卷八第五至第九頁
^ 朱載堉《樂律全書》卷八《律學新說》
^ Thomas Christensen. The Cambridge History of Western Music Theory. Cambridge University Press. 20 April 2006: 205 [2019-11-12]. ISBN 978-1-316-02548-2. （原始內容存檔於2020-02-18）.
^ Hermann Von Helmholtz, On the Sensations of Tone as a Physiological basis for the theory of music, p 258, 3rd edition, Longmans, Green, and Co., London, 1895
^ 勞漢生《珠算與實用算術》，2010年，河北科學技術出版社，389頁，ISBN 9787537518918
^ Barbour, James Murray, Tuning and temperament, a historical survey, East Lansing, Michigan State College Press, 1953

來源[編輯]

李約瑟：《中國科學技術史》第四卷第一分冊
Robert Temple：The Genius of CHINA （李約瑟《中國科學技術史》的濃縮本）
戴念祖：《朱載堉———明代的科學和藝術巨星》
程貞一著，王翼勳譯：《黃鐘大呂：中國古代和十六世紀聲學成就》（上海：上海科技教育出版社，2007）。
Cho, Gene Jinsiong. (2003). The Discovery of Musical Equal Temperament in China and Europe in the Sixteenth Century. Lewiston, NY: The Edwin Mellen Press.

參見[編輯]

[1] J. Murray Barbour Tuning and Temperament p55-56, Michigan State University Press 1951

[卓仁祥2010-2] 2.0 ^2.1 美國北德克薩斯大學音樂學院教授卓仁祥. 《從文化史角度看十二平均律的發現》. 星海音樂學院學報. 2010年, (2期) [2019-11-12]. （原始內容存檔於2020-02-18）.

[3] Simon Stevin Van de Spiegheling der singconst （頁面存檔備份，存於互聯網檔案館） 2009-6-30

[4] Thomas S. Christensen, The Cambridge history of western music theory p205, Cambridge Univerity Press

[5] 卓仁祥：《東西方文化視野中的朱載堉及其學術成就》，第十章，2009年，中央音樂學院出版社，151頁。ISBN 978-7-81096-325-1

[6] 卓仁祥：《東西方文化視野中的朱載堉及其學術成就》，第十章，2009年，中央音樂學院出版社，152頁，ISBN 978-7-81096-325-1

[7] 朱載堉維基文庫中的相關文獻：《樂律全書》卷八第五至第九頁

[8] 朱載堉《樂律全書》卷八《律學新說》

[Christensen2006-9] Thomas Christensen. The Cambridge History of Western Music Theory. Cambridge University Press. 20 April 2006: 205 [2019-11-12]. ISBN 978-1-316-02548-2. （原始內容存檔於2020-02-18）.

[10] Hermann Von Helmholtz, On the Sensations of Tone as a Physiological basis for the theory of music, p 258, 3rd edition, Longmans, Green, and Co., London, 1895

[11] 勞漢生《珠算與實用算術》，2010年，河北科學技術出版社，389頁，ISBN 9787537518918

[12] Barbour, James Murray, Tuning and temperament, a historical survey, East Lansing, Michigan State College Press, 1953

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]