十进制
| 记数系统 | |
|---|---|
| 印度-阿拉伯数字系统 | |
| 西方阿拉伯数字 阿拉伯文数字 高棉數字 孟加拉数字 |
印度數字 波羅米數字 泰语数字 |
| 漢字文化圈記數系統 | |
| 中文数字 閩南語數字 越南语数字 算筹 |
日語數字 朝鲜语數字 苏州码子 |
| 字母記數系統 | |
| 阿拉伯字母數字 亚美尼亚数字 西里爾數字 吉茲數字 |
希伯來數字 希腊数字 阿利耶波多數字 |
| 其它記數系統 | |
| 阿提卡數字 巴比倫數字 古埃及数字 伊特拉斯坎數字 |
玛雅数字 罗马数字 熙笃会数字 卡克托维克数字 |
| 依底数区分的进位制系统 | |
| 1 2 3 4 5 6 8 9 10 11 12 16 20 36 60 | |

十進位是以10爲底数的數字系统,是在世界上應用最廣泛的進位制。
十进制有两大类:
- 无位值概念的十进制:古希腊、古埃及和古印度的佉卢十进制和婆羅米十进制都属于这一类。
- 具有位值概念的十进制,特称为十进位制,如中国古代的算筹数,和印度阿拉伯数字,以及现代数学广泛使用的,由印度-阿拉伯数字发展而来的阿拉伯数字。
十进制包括十进位制,但不等同十进位制。
来源[编辑]
人類算數採用十進制,可能跟人類有十根手指有關。亚里士多德称人类普遍使用十进制,只不过是绝大多数人生来就有10根手指这样一个解剖学事实的结果。实际上,在古代世界独立开发的有文字的记数体系中,除了巴比伦文明的楔形数字为60进制,玛雅数字为20进制外,几乎全部为十进制。只不过,这些十进制记数体系并不是按位的。[1]
世界各国的数字系统[编辑]
- 无位值十进制
- 古埃及十进制:以一个竖道代表1,二并排竖道代表2,三竖道代表3,一横道代表4,左二撇右竖道代表5,上三撇下三撇代表6,上下两道代表8,四个「(」并排代表9,一个“人”字形代表10,“人”上加一横代表20,20左加一点代表30,横道上加一点代表40,横道上加三竖道(如中国筹算的8)代表60,横道上加四竖道代表80(形同中国筹算中的9)代表80,两横道上加三竖代表90……。
- 古希腊十进制,1至9,10至90,100至900各有不同的单字母代表。
- 古印度Kharosshi十进制,以一个竖道代表1,二并排竖道代表2,三竖道代表3,一个X代表4,IX代表5,||X代表6,XX代表8,10,20个有单字符代表。
- 古印度和Brahmi十进制,和希腊十进制相似,1至9,10至90,100至900各有不同的单字母代表。符号很多。
- 十进位制(有位值十进制)
- 中国古代的十进制有书写式和算筹两种型式。
- 印度-阿拉伯十进位制。
方法[编辑]
用文字表示十進整數位[编辑]
十进位制可以表示任何整數。利用小數點,還可以表示一些小數。
| n | 10n | 前綴 | n | 10n | 前綴 | n | 10n | 前綴 | n | 10n | n | 10n | n | 10n | n | 10n | n | 10n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 個 | - | 12 | 兆/萬億 | 太[2] | 24 | 秭 | 堯 | 36 | 澗 | 48 | 極 | 60 | 那由他 | 72 | 大數 | 84 | |
| 1 | 十 | - | 13 | 十兆 | - | 25 | 十秭 | - | 37 | 十澗 | 49 | 十極 | 61 | 十那由他 | 73 | 十大數 | 85 | |
| 2 | 百 | - | 14 | 百兆 | - | 26 | 百秭 | - | 38 | 百澗 | 50 | 百極 | 62 | 百那由他 | 74 | 百大數 | 86 | |
| 3 | 千 | 千 | 15 | 千兆 | 拍 | 27 | 千秭 | 容 | 39 | 千澗 | 51 | 千極 | 63 | 千那由他 | 75 | 千大數 | 87 | |
| 4 | 萬 | - | 16 | 京 | - | 28 | 穰 | - | 40 | 正 | 52 | 恒河沙 | 64 | 不可思議 | 76 | 88 | ||
| 5 | 十萬 | - | 17 | 十京 | - | 29 | 十穰 | - | 41 | 十正 | 53 | 十恒河沙 | 65 | 十不可思議 | 77 | …… | ||
| 6 | 百萬 | 兆[2] | 18 | 百京 | 艾 | 30 | 百穰 | 昆 | 42 | 百正 | 54 | 百恒河沙 | 66 | 百不可思議 | 78 | 100 | 古戈爾 | |
| 7 | 千萬 | - | 19 | 千京 | - | 31 | 千穰 | - | 43 | 千正 | 55 | 千恒河沙 | 67 | 千不可思議 | 79 | |||
| 8 | 億 | - | 20 | 垓 | - | 32 | 溝 | - | 44 | 載 | 56 | 阿僧祇 | 68 | 無量 | 80 | …… | ||
| 9 | 十億 | 吉 | 21 | 十垓 | 澤 | 33 | 十溝 | - | 45 | 十載 | 57 | 十阿僧祇 | 69 | 十無量 | 81 | 10100 | 古戈爾普勒克斯 | |
| 10 | 百億 | - | 22 | 百垓 | - | 34 | 百溝 | - | 46 | 百載 | 58 | 百阿僧祇 | 70 | 百無量 | 82 | |||
| 11 | 千億 | - | 23 | 千垓 | - | 35 | 千溝 | - | 47 | 千載 | 59 | 千阿僧祇 | 71 | 千無量 | 83 | ...... | ||
用文字表示十進小數位[编辑]
| n | 10n | 前綴 | n | 10n | 前綴 | n | 10n | 前綴 |
|---|---|---|---|---|---|---|---|---|
| 0 | 個 | - | -12 | 漠 | 皮 | -24 | 涅槃寂靜 | 幺 |
| -1 | 分 | 分 | -13 | 模糊 | - | -25 | ||
| -2 | 厘 | 厘 | -14 | 逡巡 | - | -26 | ||
| -3 | 毫 | 毫 | -15 | 須臾 | 飛 | -27 | 柔 | |
| -4 | 絲 | - | -16 | 瞬息 | - | -28 | ||
| -5 | 忽 | - | -17 | 彈指 | - | -29 | ||
| -6 | 微 | 微 | -18 | 剎那 | 阿 | -30 | 亏 | |
| -7 | 纖 | - | -19 | 六德 | - | -31 | ||
| -8 | 沙 | - | -20 | 虛空 | - | -32 | ||
| -9 | 塵 | 奈/納[2] | -21 | 清靜 | 仄 | -33 | ||
| -10 | 埃 | - | -22 | 阿賴耶 | - | -34 | ||
| -11 | 渺 | - | -23 | 阿摩羅 | - | -35 |
註:
- 厘亦作釐。
- 毫亦作毛。
- 漠是正寫,而莫並非正確寫法。
- 比漠微細的,是自天竺佛經上的數字。而這些「佛經數字」已成為古代用法了。
历史沿革[编辑]


中文自始至终都是使用十进制,没有任何使用其他进制的证据。
有学者认为,北京周口店的一万多年前的山顶洞人遗址出土的骨管,以一个圆点代表1,两个圆点并列代表2,三个圆点并列代表3,五个圆点上二下三排列代表5,长圆形可能代表十。中国著名数学史家,国际科学史研究院通讯院士李迪教授认为山顶洞人骨管符号是“一种十进制思想”[3]。
另有学者对中国青海乐都县柳湾出土一千多枚新石器时代骨片进行研究,发现它们分属马厂、半山、齐家和辛店四个中文化型。骨片长度为2-2.4厘米,厚约1毫米。骨片上有刻痕,少的一个,多不超过八个,每个骨片上的刻痕数目不超过十个,他们以此认为新石器时代已有加法运算和十进制[4]。
另有学者认为,甲骨文中一横代表1,两横相叠代表二,三横代表三,四横代表四,X 代表五,“人”形代表六,“十”代表七,“)(”代表八, “九”已经是九;| 代表十,||代表20,|||代表三十,||||代表四十;此外50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000,2000,……9000,10000……40000 都有不同的符号。商代甲骨文“已形成完整的十进制系统”。[5]
北京的中国历史博物馆藏有一把安阳殷墟出土的象牙尺,长15.78厘米,分为十寸,说明中国商代的十进制几经用在长度上了。
中国周代金文的纪数法,继承商代的十进制, 又有明显的进步,十进数量级符号有十、百、千、万、亿,如西周金文“伐鬼方……俘万三千八十一人”,“武王遂征四方,俘人三亿万有二百三十”,出现了位值记数,例如 “俘牛三百五十五“,其中三百五十五写成“三全XX”,前面的“全”是金文的“百”,后面两个XX是五十五,省去了“十”,出现了位置概念,但尚未形成完整的位值制。金文商鞅量铭还出现分数。[6]
春秋战国时代,出现严格的十进位制筹算记数,以空代表0,也发明了用于十进位制乘法、除法的九九表和《算表》。
公元前3400年左右,古埃及有基于十进制的记数法。[7]但这种十进制并无位值的概念。[8]
吠陀时代前800年的印度仪轨经类文献中的绳法经中包含大量分数的应用,但并无证据显示此时的文字记数系统是十进制的。[9]
公元前500年,希腊古典时期的阿提卡数字为十进制系统。[7]
公元前300年,印度的婆罗迷数字为十进制。[7]婆罗迷十进制毫无位值概念。
出土于巴基斯坦的古印度巴克沙利手稿可能是世界上最早的包括0的“真正的”十进制系统,[10]但它的具体时间有争议。[11]
起源[编辑]







一般“共识”认为现在世界通行的十进制起源于印度。从20世纪初,国际上许多学者,包括李约瑟在内对印度起源论提出了质疑。
- 早在1907年印度学者Kaye指出“我研究的目的,在于指出我们关于现代数学记数的基础很不牢固,值得重新研究。从印度文字,碑文证据,早期印度日的记数法,以及现代印度土著的风俗习惯等方面,指明现代记数可能来自外国[12]
- 印度学者Datta and Singh认为,“印度不存在记述这些数字及其基本算术运算方法的早期文献,发明人不可知”[13]
- 德国学者Menninger 认为印度十进制的起源,模糊不清。[14]
- 李约瑟指出,古印度的数字系统,用单独的符号表示10和10的倍数,相对于希腊或希伯来数字系统,毫无进步……印度数字中的0,很可能起源于东印度和中国南方文化接壤的地区。印度是否采纳中国算筹的空档而受启发?关键在于中国在比孙子算经早很多的时期,已经拥有十进位值制。[15]
- 曾任小学教师的法国通俗作家Ifrah断言,458年的印度耆那教文献Lokavibhaga中的 panchabhyah khalu shunyebhyah param dve sapta chambaram ekam trini cha rupam cha代表“五空和二和七和天,一和三和形,就是13107200000”,“是世界上最早的带零的十进位数字”。[16]。他还说,印度的零、一、二、……九的词多了,有eka,pitamaha,adi,tanu……都指“一”,dvi,ashvin,Yama, yamala, netra,bahu,guophau, paksha 都可以是“二”……[17]。有学者认为现在世界各国使用的阿拉伯数字都起源于这一系统。[18]
- 美国学者Robert Temple根据李约瑟《中国科学技术史》缩写的“Genius of China”,认为今日世界通行的十进制,真正起源地在中国[19]。
- 新加坡著名数学史家兰丽蓉认为阿拉伯数字的基本概念,不可能起源于印度婆罗迷数字,而是起源于中国筹算。筹算用九个符号代表一切数,其加法减法,天然包含在算筹之中,三减三就是从算版上取去三个算筹,算版上自然而然留下一个空位,这就是零,筹算中称为‘空’。无独有偶,印度在没有发明‘0’这个符号之前,和中国的筹算一摸一样,也用一格空档来表示零,称为“sunya”!,这就没有天然的理由了;而“983 542”到底是一个数字还是两个数值,容易产生混淆,后来印度才用“.”或“0”代表sunya。此外印度的加减乘除运算程序,上、中、下三行排列的方式,除数和被除数首位对齐,留筹算式的空白(!)而非“0”,从左往右计算的规则,商数右边留空白而没有补“0”,每算一步之后,除数右移一位,甚至余数表示为分数的上、中、下三行表示方法,居然和孙子算经中叙述的孙子除法雷同,这三点是印度十进位数字系统的基础概念全盘来自筹算的铁证。[20]。
现存最古老的运用印度数字的算术著作:10世纪波斯数学家伊本·拉班在所著《印度算术原理》中详细叙述的印度除法,印度开平方术,开立方术也同样源自孙子算经[21]
0……9符号来自印度,但背后的十进位制概念,则来自筹算。将空写成0,只是书写方式,没有概念上的发明。至于中国筹算十进制如何传入印度,兰丽蓉认为中国古时官员,商人僧侣和旅行家,腰挂算筹袋很平常,而中国和印度来往密切,传入印度不难理解。事实上早于458年一个半世纪,从公元266-399年间,就有竺法护,康法郎,于法蓝,竺佛念,慧常,进行,慧辩,支法领,法净等高僧到过印度了,此后还有著名的法显到过佛国。
印度与阿拉伯的十进位制[编辑]
- 七世纪之前,印度数字用一到九个符号,以空代零。[22]。时至今日,南印度泰米尔纳德邦仍通行九个符号加空代零,另有十、百、千符号[23]。
- 公元七世纪,印度Nagari数字出现0。[24]
- 公元八世纪唐朝太史监印度人瞿昙悉达在开元年间主持编纂的《开元占经》卷104将印度数字“·”(零)引入中国,“右天竺算法用上件九个字乘除,其字皆一举扎而成,凡数至十进入前位,每空位处恒安一点”,但只有文字叙述,未曾画出印度数吗的形状。[25]
- 学界公认,印度带“0”的十进位制最早出现在876年印度瓜廖尔Bhojadera碑文,“933”年印度历(公元876年)碑文文记述一块“270” 乘 “187” 的花园,每日给庙奉献“50”个花圈。[26][27]“933”、“270”、“187”、“50”四个印度数字,已经是现代阿拉伯数字了。
- 印度本土用印度数字的算术著作已荡然无存,但保留在多种阿拉伯文著作中。存世最古老的一本用印度数字的算术书,当推十世纪波斯数学家伊本·拉班所著的《印度算术原理》,他在该书第一章详细叙述印度十进位制数字的原理。他写道“必须认识九个数字۹۸۷۶۵۴۳۲۱,第一个是一,第二个是二,一直到九,并且头一个是个位,第二个是十位,第三百位,第四千位,第五万……十之后必须加一个零,一百之后必须加两个零,即记十为10,百为100。
- 九世纪花拉子米,十世纪伊本·拉班,十一世纪乌克里迪西等阿拉伯数学家都著有关于印度算术的著作,所述的加、减、乘、除、开平方、开立方的程序,从排列方式,留空方式,数字位移方式,以至余数、分数的表示格式,都和中国公元一世纪的九章算术、5世纪孙子算经所述的相应算术运算相同。中世纪的印度-阿拉伯数学家用沙盘进行计算.沙盘可以是带沙子的地面或一块木板,上铺一层薄沙,划上格子,用手指头或一根棍将阿拉伯数字划在格子里面。因为有格子,所以空格就代表零,不必写“0”[28],这和中国筹算以空代零的习惯一样[29]。
- 印度文数字的0,1,2……9中的“0”,是印度数学对十进位制的重要贡献,它克服了算筹数码空档的缺点,例如
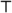 可以指6,600,60000……使十进位制草算在中世纪阿拉伯国家大为流行。
可以指6,600,60000……使十进位制草算在中世纪阿拉伯国家大为流行。 - 中国南宋数学家秦九韶在算筹码中引入圆圈
 可能受到印度“0”的影响。
可能受到印度“0”的影响。
十进制與度量衡[编辑]
傳統度量衡不是完全使用十进制,例如1斤等於16兩、1呎等於12吋等。公制完全使用十进制,使換算較直接。中華民國政府於1920年代推行市制以與公制接軌。1980年代香港政府便曾大力宣傳十进制的好處,當時有口號如「採用十进制,公道又易計」或「十进制,好易計」等,但民間至今仍常用舊制、英制等非十進制換算。
清华简算表[编辑]
成于公元前300年左右的清华简《算表》是世界上最早的十进制乘法表[31]。
美国数学史家约瑟夫·道本周(Joseph Dauben)说《算表》是世界上最早的十进制乘法表文物[31]。

参考文献[编辑]
- ^ 数学史概论,李文林,ISBN 7-04-011361-9,14页
- ^ 2.0 2.1 2.2 香港法例第214章《十進制條例》附表1
- ^ 吴文俊院士主编《中国数学史大系》第一卷 上古到西汉 127页 ISBN 7-303-04555-4/O 引李迪 《中国数学史简编》 5-6 1984
- ^ 吴文俊院士主编《中国数学史大系》第一卷上古到西汉 129页
- ^ 吴文俊院士主编《中国数学史大系》第一卷 上古到西汉 127页 ISBN 7-303-04555-4/O 144-151
- ^ 吴文俊院士主编《中国数学史大系》第一卷《上古到西汉》第三章《金文中的数学》 177页
- ^ 7.0 7.1 7.2 数学史概论,13页
- ^ 前引书,18页
- ^ 数学史概论,106页
- ^ 数学史概论,107页
- ^ Bibhutibhusan Datta (Volume 35, Number 4 (1929), 579–580.). Review: G. R. Kaye, The Bakhshâlî Manuscript—A Study in Mediaeval Mathematics, 1927. Bull. Amer. Math. Soc.. http://projecteuclid.org/euclid.bams/1183493367 (页面存档备份,存于互联网档案馆). Retrieved 2007-07-24.
- ^ Kaye, G,R, Notes On Indian Mathematics, Arithmetical notation. Journal of the Asiatic Society of Bengal
- ^ Datta & Singh, History of Hindu mathematics, Bombay,1962
- ^ Menninger:Number Words and number symbols, MIT Press 1969
- ^ 李约瑟原著 柯林·罗南改编 上海交通大学科学史系翻译 《中华科学文明史》 第二卷 第一章 数学
- ^ Ifrah, Georges (2000) The Universal History of Numbers: From Prehistory to the Invention of the Computer, Wiley. ISBN 0-471-39340-1,416页 “five voids, then two and seven,the sky, one and three and the form"
- ^ 同上410页
- ^ 数学史概论,108页
- ^ Robert Temple, The Genius of China, with preface by Joseph Needham。 139 ISBN 9781853752926。
- ^ Lam Lai Yong,A Chinese Genesis, Rewriting the history of our numeral system. Archive for History of Exact Science 38 101-108
- ^ Lam Lay Yong, Fleeting Footsteps, p44, 图i至v
- ^ George Ifrah, The Universal History of Numbers, p378-380
- ^ George Ifrah,p372
- ^ George Ifrah, p380
- ^ 吴文俊主编 中国数学史大系 卷4 418页
- ^ 李约瑟原著,柯林·罗南改编中华科学技术史 2,第一章 数学
- ^ George Ifrah,The Universal History of Numbers, From Prehistory to the Invention of Computers, P400 Wiley ISBN 0-9650455-0-1
- ^ George Ifrah, The Universal History of Numbers, p555-556, Wiley
- ^ The conceptual origins of our numeral system and the symbolic form of algebra. Archive for History of Exact Sciences 36: 183-195. Lam Lay-Yong. 1987
- ^ 30.0 30.1 法国马若安著《中算史导论》 第十二章
- ^ 31.0 31.1 The 2,300-year-old matrix is the world's oldest decimal multiplication table.自然杂志. [2014-03-12]. (原始内容存档于2019-09-13).
參見[编辑]
外部連結[编辑]
| ||||||||||||||||||||||
| |||||||||||||||||||||
|




