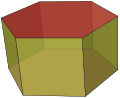
雙錐體
 以雙六角錐為例 | |||
| 類別 | 雙錐體 | ||
|---|---|---|---|
| 對偶多面體 | n角柱 | ||
| 數學表示法 | |||
| 考克斯特符號 | |||
| 施萊夫利符號 | { } + {n} | ||
| 性質 | |||
| 面 | |||
| 邊 | |||
| 頂點 | |||
| 歐拉特徵數 | F=, E=, V= (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 三角形 | ||
| 頂點圖 | V4.4.n | ||
| 對稱性 | |||
| 對稱群 | Dnh, [n,2], (*n22), order 4n | ||
| 旋轉對稱群 | Dn, [n,2]+, (n22), order 2n | ||
| 特性 | |||
| 凸、 面可遞 | |||
| 圖像 | |||
| |||
| 註:為底面邊數 。 | |||
雙錐體,或雙稜錐、又稱雙角錐,是一種幾何體,是由一錐體,經底面鏡射產生的像和原本的錐體合成的立體,換句話說,雙錐體就是將兩個相同的錐體背對背、底面對底面黏起來。其也是柱體的對偶多面體,將一柱體每面的重心當作新的頂點做成多面體也可得到雙錐體。
一般雙錐體會命名為類似雙n角錐的名稱,不是因為它有一個n邊形的面,而是因為它的橫切面是n邊形,或說它是由n角錐疊成的。
每面全等的雙n角錐是正n角體的對偶多面體,這樣子的雙錐的面通常是等腰三角形。
體積[编辑]
雙錐的體積,其中B是中央切面的面積,基座的面積;h是基座到頂點的高度。
正雙錐的體積,基座的正n邊形長度為s,基座到頂點的高度為h,則有:
詹森雙錐[编辑]
在所有雙錐中,有3個雙錐全部都由正多邊形組成,分別為雙三角錐、雙四角錐和雙五角錐;雙六角錐退化成一個平面。
雙三角錐和雙五角錐屬於詹森多面體;雙四角錐屬於正多面體,因此不屬於詹森多面體。

|

|

|
| 雙三角錐 | 雙四角錐 (正八面體) |
雙五角錐 |
參考來源[编辑]
- 埃里克·韦斯坦因. Dipyramid. MathWorld.
- Olshevsky, George, Bipyramid at Glossary for Hyperspace.
- The Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- Virtual Reality Polyhedra (页面存档备份,存于互联网档案馆) The Encyclopedia of Polyhedra
- VRML models (George Hart) (页面存档备份,存于互联网档案馆) <3> (页面存档备份,存于互联网档案馆) <4> (页面存档备份,存于互联网档案馆) <5> (页面存档备份,存于互联网档案馆) <6> (页面存档备份,存于互联网档案馆) <7> <8> (页面存档备份,存于互联网档案馆) <9> (页面存档备份,存于互联网档案馆) <10> (页面存档备份,存于互联网档案馆)
- Conway Notation for Polyhedra (页面存档备份,存于互联网档案馆) Try: "dPn", where n = 3, 4, 5, 6, ... example "dP4" is an octahedron.
- VRML models (George Hart) (页面存档备份,存于互联网档案馆) <3> (页面存档备份,存于互联网档案馆) <4> (页面存档备份,存于互联网档案馆) <5> (页面存档备份,存于互联网档案馆) <6> (页面存档备份,存于互联网档案馆) <7> <8> (页面存档备份,存于互联网档案馆) <9> (页面存档备份,存于互联网档案馆) <10> (页面存档备份,存于互联网档案馆)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||