牛頓第一運動定律

牛頓第一運動定律(Newton's first law of motion,中國大陸譯牛頓第一定律[1])又稱「慣性定律」(law of inertia)[1]。該定律表明,假若施加於某物體的外力為零,則該物體的運動速度不變。[2]根據這定律,假設沒有任何外力施加或所施加的外力之和為零,則運動中物體總保持勻速直線運動狀態,靜止物體總保持靜止狀態。物體所呈現出的維持運動狀態不變的性質稱為「慣性」。牛頓第一運動定律又稱為「慣性定律」,只成立於慣性參考系,又稱為「牛頓參考系」。[3]
1687年,英國物理泰斗艾薩克·牛頓在巨著《自然哲學的數學原理》裏,提出了牛頓運動定律,其中有三條定律,分別為牛頓第一運動定律、牛頓第二運動定律與牛頓第三運動定律。[4]
在歷史上,第一定律是古典物理最早的基石之一,在所有現代物理學裡,它是不可或缺的基礎內容。然而,很多教科書都沒能合乎邏輯地明確表述出這定律。物理學者約翰·瑞格登認為這定律是「邏輯惡夢」,但也稱譽這定律是難以形容的奧妙。[5][註 1][註 2]
概述[編輯]
牛頓第一運動定律表明,假若施加於某物體的外力為零,則該物體的運動速度不變。以方程式表達,[2]
- ;
其中, 是第 個外力, 是速度, 是時間。
從第一定律可以得到下面推論:
- 靜止的物體會保持靜止狀態,除非有外力施加於這物體。
- 運動中的物體不會改變其運動速度,除非有外力施加於這物體。注意到速度是向量,物體運動速度的大小與方向都不會改變。
根據第一定律,從測量物體的運動速度是否改變,可以判斷是否有外力作用於物體,但是,第一定律並未給出這外力的大小,也沒有給出這外力的來源,它只是將物體運動速度的改變歸因為外力的施加於物體。[8]從另一個角度來看,只有因為外力的施加於物體才會改變物體的運動,否則,物體的運動會永遠保持不變,這意味著,物體擁有某種懶於改變運動狀態的性質,稱為物體的慣性。[9]
牛頓繪景[編輯]
第一定律是物理定律,因此具有可證偽性,即做實驗可以核對第一定律是否正確。在做這實驗時,必須測量物體的運動速度,但這涉及到參考系的設定。因此,可以更詳細地將第一定律表明為[10]
採用某種參考系來做測量,假若施加於一個物體的外力為零,則該物體的運動速度不變。
儘管在《自然哲學的數學原理》裏沒有明確地指明應該怎樣詮釋作用力,從第一定律的內容可以推論,牛頓認為,零作用力案例可以很容易地被辨認出來。這案例能夠對於慣性參考系給出定義:假若,從一個參考系觀測,不受力的物體的運動速度不變,則這參考系是慣性參考系。在宇宙中,存在著無數可能的參考系,在這些參考系中,滿足第一定律的參考系稱為「慣性參考系」,而其它不滿足第一定律的參考系稱為「非慣性參考系」。因此,第一定律可以被視為慣性參考系的定義。從做實驗觀察物體的運動行為,就可以辨別出哪個是慣性參考系,哪個不是慣性參考系。[11]至今為止,多個位於地球表面固定地點的實驗室所完成的眾多關於古典力學的實驗建議,這些實驗室很適合實現慣性參考系,對於那些不合適的實驗,則必須設計與建造更為精緻的實驗室。[10]
在做實驗核對第一定律時,還必須測量是否有外力施加於物體,這意味著必須對於力給出嚴格定義。牛頓在《自然哲學的數學原理》裏提出第一定律後,又列舉了三個描述外力與物體運動狀態之間的關係的案例,它們分別為空氣阻力與重力的施加於拋體、空氣阻力與黏力的施加於陀螺、行星與彗星的移動於自由空間。牛頓還給出了三種外力,分別為衝擊力、壓力與離心力。但是他並沒有對於力給出嚴格定義。[4][註 3]

使用操作定義的方法可以對於力給出嚴格定義,例如,兩個同樣的彈簧,假若被壓縮同樣的距離,則其各自產生的「彈力」(一種物理現象)必定相等,將這兩個彈簧並聯,則可以產生兩倍的彈力。將一物體的兩邊分別連接這兩個彈簧的末端,使彈力的作用方向相反,則作用於物體的淨力為零,為了對於彈力給出定量描述,設定「標準單位力」為某特定彈簧壓縮特定距離所產生的彈力,任意數量的標準單位力都可以用幾個彈簧所組成的系統來實現。彈簧系統可以用來做測量實驗,對於任意力做比較,給出它的測量值。[11][15]
克希荷夫繪景[編輯]
另外還有一種常見的繪景是由古斯塔夫·克希荷夫最先給出,後來又獲得恩斯特·馬赫、海因里希·赫茲等人的支持。按照這種繪景,第一定律被視為第二定律的零外力特別案例,[註 4]而第二定律則被視為力的定義,即將力定義為質量與加速度的乘積。[註 5]這樣,就不必涉及引入力的概念這棘手的任務。假若採用這種繪景,則第二定律不再擁有任何物理內涵,[6]而牛頓並沒有發現力是質量與加速度的乘積,因為這只是一個定義,牛頓發現的是,物理定律比較容易用力的概念來表達。[11]
這種繪景會導致的後果是,整個古典力學會變成一種公理化理論,所有結論都是源自於這個定義,而不是源自於更為物理學者青睞的從做實驗總結出的「自然定律」。假若要將實際物理引入這公理化理論,則必須檢試對於力的定義所推導出的結果是否符合實際物理,只有符合實際物理才可被採納,換句話說,從對於力的定義所演繹出的規則,其結果必須符合實驗的檢試,否則不能被採納。[11]
只有從某種特定的參考系觀測,才可以將牛頓定律與實際物理接軌,這種特定的參考系就是慣性參考系,通過做實驗可以找到無限數量的這種慣性參考系。從任何其它種參考系觀測,都無法達成接軌的目標。更具體而言,只有從慣性參考系才可觀測到不受力物體的運動速度不變。[11]
愛因斯坦繪景[編輯]
阿爾伯特·愛因斯坦的等效原理指出,對於一位處於重力場的觀察者呈靜止狀態與一位不處於重力場的觀察者呈加速度運動狀態而言,假若這兩位觀察者感受到的力相等,則他們會無法分辨到底感受到的是重力還是因加速度而產生的慣性力(注意到慣性力的方向與加速度的方向相反,慣性力抗拒加速度運動)。任何處於重力場的自由落體都不會感受到重力,因為,重力已與自由掉落的加速度運動所出現的慣性力相互抵銷,因此,假設從某個參考系觀察到這自由落體呈靜止狀態或或等速直線運動,則這參考系滿足第一定律,這參考系是慣性參考系。由此可採用一種新的觀點,即與處於重力場的自由落體呈靜止狀態或等速直線運動的參考系為慣性參考系,而第一定律適用於此慣性參考系。一個物體的無重量現象可以用來辨明慣性參考系。[11][17]
歷史[編輯]
亞里斯多德認為,在宇宙裏,所有物體都有其「自然位置」──處於完美狀態的位置。物體會固定不動地處於其自然位置。被移離其自然位置的物體,會傾向於返回其自然位置。這是因為物體傾向於完美狀態的位置。因此,像石頭一類的重物體傾向於朝著地面移動,像菸灰一類的輕物質傾向於朝著包含月亮在內的區域移動。亞里斯多德仔細地區分了兩種運動,「自然運動」與「暴烈運動」(violent motion)。重物體的自由墜落是一種自然運動,而發射體的運動則是非自然運動。處於自然位置的物體傾向於固定不動,只有施加「暴烈力」(violent),才能將物體移離其自然位置。所有暴烈運動都不具有永久性,遲早會終止結束。為了維持暴烈運動,必需繼續地施加暴烈力於物體,使其移離自然位置。[18]不處於自然位置的任意物體,在被釋放後,會很快地達到其最終速度,然後維持這速度直到移動至它的自然位置。[19]
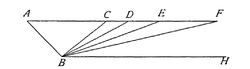
伽利略·伽利萊的想法大不相同。伽利略提出的慣性定律表明,只有施加外力,才能改變物體速度;維持物體速度不變,不需要任何外力。為了證實他的主張是正確的,伽利略做了一個思想實驗。如右圖所示,讓靜止的圓球從點A滾下斜面AB,滾到最底端後,圓球又會滾上斜面BC,假設兩塊斜面都非常的平滑、摩擦係數爲零,而且無空氣阻力,則圓球會滾到與點A同高度的點C;對於斜面BD、BE或BF,儘管圓球的滾動距離會變得越來越長,圓球也同樣地會滾到與點A同高度的位置;假設斜面是水平面BH,則該圓球永遠不能滾到先前的高度,因此會不停地呈等速直線運動。伽利略總結,運動中的物體會持續地以等速直線運動,假若不碰到任何阻礙。[20]伽利略的慣性定律對於動力學的基礎做出重大貢獻,並且徹底地推翻了多年來學者們研讀的亞里斯多德理論,因此促使十七世紀學者們產生極大的困惑,但他並沒有建構出一個新的替代理論,這還有待後來牛頓的貢獻。[21]
勒內·笛卡爾在1644年著作《哲學原理》裏提出了三條自然定律。第一條自然定律表明,假若不將其它影響納入考量,則每個物體永遠會處於同樣的狀態,假若它是處於移動狀態,則它會永久持續的移動。第二條自然定律表明,所有只倚靠內在因素的運動都是直線運動。在這兩條自然定律裡,笛卡爾確切聲明,動態與靜態是物體的兩種基本狀態,只有當承受到外在因素作用,物體的基本狀態才會有所改變。笛卡爾版本的慣性定律對於現代動力學理論的奠基助益良多。牛頓很早就意識到笛卡爾狀態概念的基礎性。[16][22]
1673年,克里斯蒂安·惠更斯發表了著作《擺鐘論》。這本牛頓非常欣賞的著作採用更明晰的邏輯架構,重新推導出了伽利略的自由落體理論。惠更斯對於物體的運動提出了三個假設。第一個假設是惠更斯版本的慣性定律。第一個假設表明,假設重力不存在,假設空氣不會阻礙物體的運動,則任意物體的運動會是持續的直線等速運動。[16][23]

伽利略的想法導致牛頓第一定律誕生──不施加外力,則沒有加速度,因此物體會維持速度不變。牛頓將第一定律的想法歸功於伽利略。第一定律其實是伽利略所提出的慣性定律的再次陳述。[註 6][24]原版第一定律的英文翻譯為[4]
Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
中文翻譯為
物體會堅持其靜止或等速直線運動狀態,除非有外力迫使改變其狀態。
寫出第一定律後,牛頓開始描述他所觀察到的各種物體的自然運動。像飛箭、飛石一類的發射體,假若不被空氣的阻力抗拒,不被重力吸引墜落,它們會持續不停地運動。當陀螺旋轉時,陀螺內部的組成粒子,如果沒有被黏合在一起,就會沿著旋轉曲線的切線以直線運動飛奔離開。由於這些組成粒子被黏合在一起,假若不受到地面摩擦力與空氣阻力的損耗,它們會永久不息地共同隨著陀螺旋轉。像行星、彗星一類的星體,移動於阻力較小的自由空間,會更長時期地維持它們的運動軌道。在這裏,牛頓並沒有提到第一定律與慣性參考系之間的關係,他所專注的問題是,為什麼在一般觀察中,物體的運動狀態會被改變?他認為原因是有空氣阻力、地面摩擦力等等作用於物體。假若這些力不存在,則運動中的物體會永遠不停的做等速直線運動。[4]
似乎還有好幾位其它自然哲學家與科學家分別獨立地想出了慣性定律。[註 7]
慣性參考系[編輯]
當描述物體運動時,只有相對於特定的物體、觀察者或者時空坐標,才能確實顯示出其物理行為。這些特定的標識稱為參考系。假若選擇了不適當的參考系,則相關的運動定律可能會比較複雜,在慣性參考系中,力學定律會展現出最簡單的形式。從慣性參考系觀察,任何呈勻速直線運動的參考系,也都是慣性參考系,否則是「非慣性參考系」。換句話說,牛頓定律滿足伽利略不變性,即在所有慣性參考系裏,牛頓定律都保持不變。[25][26]
牛頓將第一定律建立在一個所謂的絕對時空,其不依賴於外界任何事物而獨自存在的參考系。[註 8]絕對時空是一個地位獨特的絕對參考系。在絕對時空中,自由物體具有保持原來運動狀態的性質。這性質稱為慣性。因此,第一定律又稱為「慣性定律」。但以現代物理學的觀點看來,並不存在一個地位獨特的絕對參考系。
在牛頓時期,固定星體時常被用為參考系,這是因為,相對於絕對空間,它們大致靜止不動。在那些相對於固定星體呈靜止不動或等速直線運動的參考系中,牛頓運動定律被認為正確無誤。但是,學者們現在知道,固定星體並不是固定不動。在銀河系內的固定星體會隨著整個星系旋轉,顯示出自行;而那些在銀河系外的固定星體會從事它們自己的運動,這可能是因為宇宙膨脹、本動速度等等。[27] [註 9]現在,慣性參考系的概念不再倚賴絕對空間或固定星體。替而代之,根據在某參考系中物理定律的簡易性質,學者可以辨識這參考系是否為慣性參考系。更確切而言,假若虛設力不存在,則這參考系是慣性參考系;否則,不是慣性參考系。[29][註 10]
實際而言,雖然不是必要條件,選擇以固定星體來近似慣性參考系,造成的誤差相當微小。例如,地球繞著太陽的公轉所產生的離心力,比太陽繞著銀河系中心的公轉所產生的離心力,要大三千萬倍。所以,在研究太陽系中星體的運動時,太陽是一個良好的慣性參考系。[31]
參閱[編輯]
註釋[編輯]
- ^ 根據第一定律,假設沒有感受到任何外力,則物體的運動速度不變。怎樣才能確定物體沒有感受到任何外力?對於這一問題,人們通常會這樣回答:「如果一個物體的運動速度不變,則這物體沒有感受到任何外力。」可是,這答案很明顯地有嚴重瑕疵。[6]
- ^ 阿爾伯特·愛因斯坦在著作《相對論的意義》裏指出,慣性定律的弱點在於涉及到循環論證: 如果一個質點離其它物體足夠遠,則這質點不呈加速度運動;而由於觀測到這質點不呈加速度運動,所以人們才斷定它離其它物體足夠遠。[7]
- ^ 牛頓對於外力給出的定義為,施加於任何物體的作用會改變該物體的狀態,不論是處於靜止狀態,或是處於等速直線運動狀態。牛頓將慣性力定義為,物體所擁有的一種抗拒的本領,其盡量使物體保持現有的狀態,不論是靜止狀態,或是等速直線運動狀態。[12]這兩個定義共同地意味了第二定律的內涵。[13]牛頓不會沒有注意到這重複部分,他這樣做必定有他的原因。為了簡確論述,本條目不探討牛頓的原因,本條目忽略並繞過這問題,另外給出嚴格定義。
- ^ 牛頓學專家薄納德·柯恩認為,牛頓之所以不合併這兩條定律為一條定律,主要的原因之一是,在牛頓那時期以及之前多個世紀的學者們普遍主張,物體的各種運動都需要外力的施加。為了推翻這根深蒂固的錯誤見解,必須特別強調第一定律所傳達的資訊,因此,牛頓不願意將第一定律併入為第二定律的特別案例。[16]
- ^ 由於物體的加速度與觀測者的參考系有關,因此須找到慣性參考系才能測量出正確的加速度,否則,牛頓定律無法與實際物理相符合。
- ^ 歷史學者並未發現牛頓曾經閱讀過伽利略的著作《論兩種新科學及其數學演化》,他應該是從閱讀其它書籍獲得到相關知識。[16]
- ^ 英國政治哲學家托馬斯·霍布斯在著作《利維坦》裏這樣陳述:
當物體靜止不動時,除非有甚麼事件將它攪動,它會永遠靜止不動。沒有人會懷疑這真理。但是當物體在運動中,除非有甚麼事件將它停止,它會永遠地運動。雖然理由相同(沒有任何東西可以改變自己),這論點並不是很容易讓人信服。
- ^ 牛頓這樣寫:「絕對、真實而數學的時間,因其自秉性質,會穩定地持續流逝,與外界任何事物無關。相對的、表觀的和通常的時間是,對於絕對時間,某種合理的、外界的量度,而這量度是通過運動方式來進行,而不是通過像小時、月、年等等真實時間。絕對空間,就其本質而言,與外界任何事物無關,並且永久保持同樣而不變動。相對空間是絕對空間的可動維度或可動量度。」Newton 1846,第77頁
- ^ 仙女座星系與銀河系之間正在以117 公里/每秒的速度互相接近對方,預計在五十億至一百億年後會發生星系碰撞。[28]
- ^ 利用牛頓第三定律,可以察覺某道力是否是虛設力。假設一個物體感受到實在的作用力,則必定會有一道對應的大小相等、方向相反的反作用力源自於這物體並且施加於另一個物體。[30]
參考資料[編輯]
- ^ 1.0 1.1 物理學名詞審定委員會.物理學名詞 [S/OL].全國科學技術名詞審定委員會,公布. 3版.北京:科學出版社, 2019: 20. 科學文庫.
- ^ 2.0 2.1 Halliday, Resnick & Walker 2005,第88-89頁
- ^ Santavy, I., Newton's first law, European Journal of Physics, 1986, 7 (2): 132–133, doi:10.1088/0143-0807/7/2/011
- ^ 4.0 4.1 4.2 4.3 Newton 1846,第83-93頁
- ^ Pfister, Herbert, Newton's First Law Revisited, Foundations of Physics Letters, 2004, 17 (1): 49–64, doi:10.1023/B:FOPL.0000013003.96640.79,
Newton's first law … was historically one of the first cornerstones of classical physics, … Neverthesis, in most mechanics textbooks little care is devoted to a logically clear formulation of Newton's first law. … John S. Rigden calls Newton's first law a 「logician's nightmare,」 but also expresses the biew that the law is a 「wonder beyond description」
- ^ 6.0 6.1 Rigden, John, High thoughts about Newton's First Law, American Journal of Physics, 1998, 55 (4): 297, doi:10.1119/1.15191
- ^ Einstein 1922,第62頁
- ^ 馬克士威 1878,第27頁
- ^ Holton & Brush 2001,第108-109頁
- ^ 10.0 10.1 French 1971,第162-163頁
- ^ 11.0 11.1 11.2 11.3 11.4 11.5 O'Sullivan, Colm, Newton's Laws of Motion: Some interpretations of the formalism, American Journal of Physics, 1980, 48 (2): 131–133 [2018-08-13], doi:10.1119/1.12186, (原始內容存檔於2019-05-02)
- ^ Newton 1846,第73-74頁
- ^ Hesse 2008,第134-135頁, it is significant that the law of inertia is already implied in his definitions of inertial force and impressed force.
- ^ French 1971,第128-129頁
- ^ Cohen 2011,第30頁, As the unit of force we choose some elementary, reproducible push or pull. This could, for example, be exerted by a standard spring stretched by a standard amount at a standard temperature.
- ^ 16.0 16.1 16.2 16.3 Cohen 2002,第68-70頁
- ^ Graneau & Graneau 2006,第175-176頁
- ^ Dugas 1988,第19-22頁
- ^ Frautschi 1986,第13-14頁
- ^ Mach 2010,第140-141頁
- ^ Frautschi 1986,第111-112頁
- ^ Slowik 2005
- ^ Huygens, Christian. Horologium Oscillatorium (An English translation by Ian Bruce). August 2013 [14 November 2013]. (原始內容存檔於2020-07-28).
- ^ Dugas 1988,第200-207頁
- ^ Landau & Lifshitz 1960,第4-6頁
- ^ Thornton 2004,第53頁
- ^ Balbi 2008,第59頁
- ^ Abraham Loeb, Mark J. Reid, Andreas Brunthaler, Heino Falcke. Constraints on the proper motion of the Andromeda galaxy based on the survival of its satellite M33 (PDF). The Astrophysical Journal. 2005, 633 (2): 894–898 [2011-11-30]. Bibcode:2005ApJ...633..894L. arXiv:astro-ph/0506609
 . doi:10.1086/491644. (原始內容存檔 (PDF)於2017-08-11).
. doi:10.1086/491644. (原始內容存檔 (PDF)於2017-08-11).
- ^ Stachel 2002,第235-236頁
- ^ Kleppner & Kolenkow 2013,第55頁
- ^ Graneau & Graneau 2006,第147頁
- ^ Walter Lewin. Newton's First, Second, and Third Laws. MIT Course 8.01: Classical Mechanics, Lecture 6. (ogg) (videotape). Cambridge, MA USA: MIT OpenCourseWar. 事件發生在 0:00–6:53. September 20, 1999 [December 23, 2010] (英語).
參考書籍[編輯]
- Einstein, Albert, The Meaning of Relativity (PDF), PRINCETON UNIVERSITY PRESS, 1922 [2019-03-27], ISBN 978-1542694247, (原始內容存檔 (PDF)於2019-03-27)
- Cohen, I., Newton's concept of force and mass, with notes on the Laws of Motion, Cohen, I.; Smith, George (編), The Cambridge Companion to Newton, Cambridge University Press, 2002, ISBN 0-521-65177-8
- Cohen, Michael, Classical Mechanics: a Critical Introduction, Michael Cohen, 2011 [2019-01-24], (原始內容存檔於2019-01-24)
- Dugas, R., A History Of Mechanics, New York: Dover Publications, Inc., 1988, ISBN 0-486-65632-2
- Frautschi, Steven, The Mechanical universe: mechanics and heat illustrated, Cambridge University Press, 1986, ISBN 9780521304320
- French, Anthony, Newtonian Mechanics, 1971
- Graneau, Peter; Graneau, Neal, In the Grip of the Distant Universe: The Science of Inertia, World Scientific, 2006, ISBN 978-981-256-754-3</ref>
- Halliday, David; Resnick, Robert; Walker, Jerl, Fundamental of Physics 7th, USA: John Wiley and Sons, Inc., 2005, ISBN 0-471-23231-9
- Hesse, Mary, Forces and Fields, A Study of Action at a Distance in the History of Physics, Philosophical Library, 2008, ISBN 978-0806530857
- Holton, Gerald; Brush, Stephen, Physics, the Human Adventure 2nd, USA: Princeton University Press, 2001, ISBN 0-8135-2908-5
- Kleppner, Daniel; Kolenkow, Robert, An Introduction to Mechanics 2nd, Cambridge University Press, 2013, ISBN 9780521198110
- Landau, L. D.; Lifshitz, E. M., Mechanics, Pergamon Press, 1960
- Mach, Ernst, The science of mechanics; a critical and historical account of its development, Watchmaker Publishing, 2010 [1919], ISBN 978-1603863254
- 馬克士威, 詹姆斯, Matter and Motion, D.Van Nostrand, 1878
- Newton, Isaac, Newton's Principia : the mathematical principles of natural philosophy, New York: Daniel Adee, 1846 請上網閱讀作者Andrew Motte的英文翻譯。
- Slowik, Edward, Descartes' Physics, Stanford Encyclopedia of Philosophy, 2005, (原始內容存檔於2019-04-29)
- Stachel, John, Einstein from "B" to "Z", Springer, 2002, ISBN 0817641432
- Thornton, Marion, Classical dynamics of particles and systems 5th, Brooks/Cole, 2004, ISBN 0534408966
外部連結[編輯]
| ||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||








