双五角锥
外观
 | ||||
| 类别 | 双角锥 Johnson多面体 J12 - J13 - J14 | |||
|---|---|---|---|---|
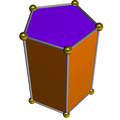
| 对偶多面体 | 五角柱 | |||
| 识别 | ||||
| 鲍尔斯缩写 | pedpy | |||
| 数学表示法 | ||||
| 考克斯特符号 | ||||
| 施莱夫利符号 | {}+{5} ft{2,5} | |||
| 康威表示法 | dP5 J13 | |||
| 性质 | ||||
| 面 | 10 | |||
| 边 | 15 | |||
| 顶点 | 7 | |||
| 欧拉特征数 | F=10, E=15, V=7 (χ=2) | |||
| 组成与布局 | ||||
| 面的种类 | 三角形 | |||
| 顶点图 | V4.4.5 | |||
| 对称性 | ||||
| 对称群 | D5h, [5,2], (*225), order 20 | |||
| 旋转对称群 | D5, [5,2]+, (225), order 10 | |||
| 特性 | ||||
| 凸、面可递、(三角面) | ||||
| 图像 | ||||
| ||||
在几何学中,双五角锥是指以五边形做为底的双锥体,其为五角柱的对偶。所有双五角锥都有10个面,15个边和7个顶点[1]。所有双五角锥都是十面体。若一个双五角锥的基底为正五边形则可称为双正五角锥或正五角双锥,若其每个面都是正多边形且以正五边形为基底,则为92种詹森多面体(J13)中的其中一个,也是双角锥的其中一种。顾名思义,它可由詹森多面体中两个大小相同的正五角锥以正五边形面接合而成。这92种詹森多面体最早在1966年由詹森·诺曼(Norman Johnson)命名并给予描述。
正五角双锥是由10个顶角40.42°、底角 69.79°、边常比的等腰三角形所构成。
若不考虑每个面皆为正五边形,只考虑基底为正五边形时,则有可能为广义的半正多面体的对偶,正五角柱的对偶,此时能使用施莱夫例符号表示,计为{ } + {5},而在考克斯特符号中,则可以用![]()
![]()
![]()
![]()
![]() 或表示。
或表示。
对偶多面体
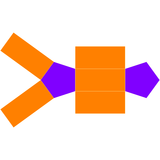
[编辑]双五角锥的对偶多面体是五角柱,但詹森多面体双五角锥的对偶多面体不是一个正五角柱,是一种七面体由五个矩形和二个五边形组成。
| 双五角锥的对偶 | 对偶的展开图 |
|---|---|

|
|
相关多面体与镶嵌
[编辑]双五角锥可以由五角形二面体透过五角化变换构造而来,因此与五角形二面体具有相同的对称性,其可以衍生出一些相关的多面体:
| 对称群:[5,2], (*522) | [5,2]+, (622) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|

|

|

| ||||||
| {5,2} | t{5,2} | r{5,2} | 2t{5,2}=t{2,5} | 2r{5,2}={2,5} | rr{5,2} | tr{5,2} | sr{5,2} | ||
| 半正对偶 | |||||||||

|

|

|

|

|

|

| |||
| V52 | V102 | V52 | V4.4.5 | V25 | V4.4.5 | V4.4.10 | V3.3.3.5 | ||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|
|||||||
| 作为球面镶嵌 | ||||||||||||

|

|

|

|

|

|

|

|

|

|

|
||
参见
[编辑]参考文献
[编辑]- ^ Pugh, Anthony, Polyhedra: A Visual Approach, University of California Press: 21, 27, 62, 1976 [2014-06-23], ISBN 9780520030565, (原始内容存档于2014-07-09).