古希臘數學
外觀
維基百科,自由的百科全書
(重新導向自希臘數學)
古希臘人是數學的奠基者,古希臘的數學在數學史中佔有頭等重要的地位。古希臘人提出了公理化體系、形式邏輯,使用邏輯證明、演繹法,強調量化和系統化,使數學成為一門嚴密的系統的富有邏輯性的學科,開啟了後世數學和科學的大門,現在世人所使用的數學和科學方法絕大部分直接來源於古希臘。
特點
[編輯]與其他文明不同的是,古希臘人的數學強調形式邏輯、演繹法、證明、公理化體系,這些理論、方法都是由古希臘人獨立並唯一地創造的。其他文明並未產生形式邏輯、演繹、公理化體系,並且並不重視證明,更缺乏公理化、系統化。現代數學、科學的理論、方法絕大部分直接來源於古希臘。因此,古希臘是數學乃至科學的奠基者,對數學的貢獻佔有最重要的地位。與古希臘相比,總體而言,其他文明的數學存在許多不足,特別是缺乏形式邏輯,因此在現代文明中,古希臘文明及其繼承者是數學與科學文明的奠基者。
來源
[編輯]古希臘數學家很願意到外國學習,他們受到巴比倫和古埃及影響很大,例如最早的古希臘數學家泰勒斯,以其命名的泰勒斯定理很可能就是他在巴比倫時學到的。而另一數學家畢達哥拉斯則在埃及留學過。
時期
[編輯]- 從伊奧尼亞學派到柏拉圖學派為止,約為公元前七世紀中葉到公元前三世紀;
- 亞歷山大前期,從歐幾里得起到公元前146年,希臘陷於羅馬為止;
- 亞歷山大後期,是羅馬人統治下的時期,結束於641年亞歷山大被阿拉伯人佔領。
著名古希臘數學家
[編輯]- 丟番圖,被譽為代數學之父。
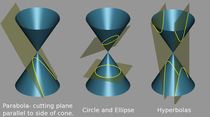
- 阿波羅尼奧斯,圓錐曲線的研究。
- 歐幾里得,著有《幾何原本》,提出了公理化體系,使用邏輯證明,奠定了後世數學的嚴密基礎。該書為任何學習數學之人的必讀標準教科書長達兩千多年。直到今天,全世界的小學、初中數學教科書中關於幾何的內容,幾乎全部來自《幾何原本》。
- 畢達哥拉斯學派,發現並證明多個定理,包括畢達哥拉斯定理。該學派學者最早發現無理數,但出於哲學原因,後來卻否認無理數的存在。
- 阿基米德,帶動幾何發展,善用窮竭法、趨近觀念(十分接近現代的微積分)。
- 柏拉圖等人,發現並證明世界上只存在五種正多面體(即柏拉圖體)。
哲學對數學的影響
[編輯]古希臘人將哲學思想帶進數和幾何形狀中,例如認為完美數是完美的、其中四個正多面體是四元素的構造、世界是用數造成的……這些概念。
哲學家柏拉圖對數學相當重視,認為數學在教育相當重要,又認為幾何是永恆的。他提出了倍平方問題。
哲學對數學的壞影響
[編輯]主條目:第一次數學危機
- 因為古希臘人對無限的恐懼,令窮竭法和趨近的方法這些和微積分相差不遠的方法發展受礙。
- 畢達哥拉斯對整數和分數的迷信令無理數的發現者死去。
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
隱藏分類: