拉普拉斯-龙格-楞次矢量

在這篇文章內，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 $\mathbf{r}\,\!$ 表示；而其大小則用 $r\,\!$ 來表示。

跳过字词转换说明

在經典力學裏，拉普拉斯-龍格-冷次向量（簡稱為 LRL 向量）主要是用來描述，當一個物體環繞著另外一個物體運動時，軌道的形狀與取向。典型的例子是行星的環繞著太陽公轉。在一個物理系統裏，假若兩個物體以萬有引力相互作用，則 LRL 向量必定是一個運動常數，不管在軌道的任何位置，計算出來的 LRL 向量都一樣 ；也就是說， LRL 向量是一個保守量。更廣義地，在克卜勒問題裏，由於兩個物體以連心力相互作用，而連心力遵守平方反比定律，所以，LRL 向量是一個保守量。

氫原子是由兩個帶電粒子構成的。這兩個帶電粒子以遵守庫侖定律的靜電力互相作用．靜電力是一個標準的平方反比連心力。所以，氫原子內部的微觀運動是一個克卜勒問題。在量子力學的發展初期，薛丁格還在思索他的薛丁格方程式的時候，沃爾夫岡·包立使用 LRL 向量，關鍵性地導引出氫原子的發射光譜。這結果給予物理學家很大的信心，量子力學理論是正確的。

在經典力學與量子力學裏，因為物理系統的某一種對稱性，會產生一個或多個對應的保守值。 LRL 向量也不例外。可是，它相對應的對稱性很特別；在數學裏，克卜勒問題等價於 一個粒子自由地移動於 四維空間的三維球面；所以，整個問題涉及四維空間的某種旋轉對稱。

拉普拉斯-龍格-冷次向量是因皮埃爾-西蒙·拉普拉斯，卡爾·龍格，與威爾漢·冷次而命名。它又稱為拉普拉斯向量，龍格-冷次向量，或冷次向量。有趣的是，LRL 向量並不是這三位先生發現的！這向量曾經被重複地發現過好幾次。它等價於天體力學中無因次的離心率向量。發展至今，在物理學裏，有許多各種各樣的 LRL 向量的推廣定義；牽涉到狹義相對論，或電磁場，甚至於不同類型的連心力。

概論

在一個物理系統裏，在任意保守的連心力的作用下（參閱保守力），一個粒子的運動，都會擁有至少四個運動常數；能量與角動量 $\mathbf{L}$ 的三個分量皆為運動常數。粒子的軌道被限制於一個平面。粒子的動量 $\mathbf{p}$ 和從力中心點的位置到粒子位置的位移 $\mathbf{r}$ （參閱圖 1）。粒子的運動平面垂直於角動量 $\mathbf{L}$ 。用方程式表示，

$\mathbf{r}\cdot\mathbf{L}=0$ 。

LRL 向量 $\mathbf{A}$ ，也肯定地包含於粒子的運動平面。可是，只有當連心力遵守平方反比定律時， $\mathbf{A}$ 才是常數向量。對於別種連心力， $\mathbf{A}$ 不是常數向量，其大小與方向都會改變。假若連心力近似地遵守平方反比定律，則 $\mathbf{A}$ 的大小近似常數，而方向會緩慢地轉動。對於所有的連心力，我們可以定義一個廣義 LRL 向量，但是，這廣義向量通常並沒有解析解，假若有，也會是一個非常複雜的函數。

歷史

在重要的克卜勒問題中， LRL 向量 $\mathbf{A}$ 是一個運動常數，時常用來描述天文軌道，例如行星的運動。然而，物理學家對它並不熟悉，這很可能是因為與動量與角動量相比，它比較難以被直覺地理解內涵的物理。因此，在過去三個世紀裏，它曾被重複地發現過許多次。1710 年，在一個不著名的義大利學刊裏，雅各布·赫爾曼最先發表了關於 LRL 向量的論文。在導引一個軌道方程式的過程中，他計算出 LRL 向量的大小， A 是保守的；並且導引出此案例與橢圓軌道離心率的關係。稍後，赫爾曼把這結果告訴约翰·白努利，他的恩師。白努利又更進一步地導引出 LRL 向量的方向。這樣，LRL 向量得到了它的現代形式。所以，不容質疑地，LRL 向量是赫爾曼和白努利共同發現的。

在那個世紀末尾，皮埃爾-西蒙·拉普拉斯又重新地發現了 LRL 向量的保守性；稍微不同地，他的導引使用的是分析方法，而不是幾何方法。十九世紀中葉，威廉·哈密頓導引出全等的離心率向量。他用離心率向量來證明，在平方反比連心力作用下，速端曲線顯示出，粒子動量向量的頭部呈圓形移動 （參閱圖 3）。二十世紀初，約西亞·威拉德·吉布斯，應用向量分析，導引出同樣的向量。後來，卡爾·龍格將吉布斯的導引，納入自己所寫的一本廣受歡迎的，關於向量的，德文教科書內，成為其中的一個例題 。1924 年，威爾漢·冷次發表了一篇關於氫原子的舊量子論的論文。在這篇論文中，他引用龍格所寫的教科書的例題為參考。1926 年， 沃爾夫岡·包立用 LRL 向量與矩陣力學，而不是薛丁格方程式，來導引氫原子的光譜。這傑作說服了大多數物理學家，使他們覺得量子力學理論是正確的。

數學定義

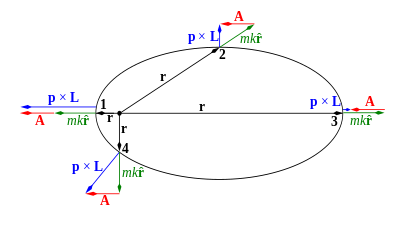
圖 1:在平方反比連心力的作用下，一個移動中的粒子，在橢圓軌道的四點（標記為 1, 2, 3, 與 4 ）的 LRL 向量 $\mathbf{A}$ （紅色表示）。力中心點表示為一個小黑點；從這黑點，位置向量 $\mathbf{r}$ （黑色表示）以徑向方向指出。角動量 $\mathbf{L}$ 垂直於軌道的平面。共面的向量 $\mathbf{p}\times\mathbf{L}$ 與 $mk\hat{\mathbf{r}}$ 分別用藍色與綠色表示。LRL 向量 $\mathbf{A}$ 是一個運動常數向量

平方反比連心力 $\mathbf{F}(r)$ 可以表達為

$\mathbf{F}(r)= - \frac{k}{r^{2}}\mathbf{\hat{r}}$ ；

其中，k 是比例常數，$\mathbf{\hat{r}} = \frac{\mathbf{r}}{r}$ 是單位向量，$\mathbf{r}$ 是粒子的位置向量，r 是 $\mathbf{r}$ 的大小。

感受到此力的作用，一個粒子的軌道運動，其 LRL 向量的數學定義方程式為

$\mathbf{A} = \mathbf{p} \times \mathbf{L} - m k \mathbf{\hat{r}}$；

其中，m 是粒子的質量，$\mathbf{p}$ 是動量，$\mathbf{L} = \mathbf{r} \times \mathbf{p}$ 是角動量。

由於平方反比連心力為保守力，能量 $E=\frac{p^{2}}{2m} - \frac{k}{r}$ 是運動常數：

$\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{p}{m}\dot{p} + \frac{k}{r^2}\dot{r}=0$。

再者，角動量 $\mathbf{L}$ 也是保守的，可以決定粒子移動平面的取向。因為 $\mathbf{p}\times\mathbf{L}$ 與 $\mathbf{r}$ 都垂直於 $\mathbf{L}$ ，所以，LRL 向量 $\mathbf{A}$ 垂直於角動量； $\mathbf{A}$ 包含於軌道的平面。

這個單獨粒子的 LRL 向量定義，也可以延伸至像克卜勒問題一類的二體問題。我們只需要設定質量 m 為二個物體的約化質量，設定位置向量 $\mathbf{r}$ 為二個物體之間的相對位置向量。

同樣的運動常數可以有很多種不同的表述．最常見的一種牽涉到離心率向量。定義離心率向量 $\mathbf{e}$ 為 LRL 向量與 mk 的除商：

$\mathbf{e} = \frac{\mathbf{A}}{m k} = \frac{1}{m k}(\mathbf{p} \times \mathbf{L}) - \mathbf{\hat{r}}$ 。

克卜勒軌道導引

圖 2：這是圖 1 的簡化版，角 θ 定義為 $\mathbf{A}$ 與 $\mathbf{r}$ 之間的夾角。

克卜勒問題的運動軌道，其形狀與取向，可以用 LRL 向量決定。 $\mathbf{A}$ 與 $\mathbf{r}$ 的內積為

$\mathbf{A}\cdot\mathbf{r}=Ar\cos\theta=\mathbf{r}\cdot\left(\mathbf{p}\times\mathbf{L} \right) - mkr$ ；

其中， θ 為 $\mathbf{A}$ 與 $\mathbf{r}$ 之間的夾角。

置換其三重積，

$\mathbf{r} \cdot\left(\mathbf{p}\times \mathbf{L}\right) = \mathbf{L}\cdot\left(\mathbf{r} \times \mathbf{p}\right) = \mathbf{L}\cdot\mathbf{L}=L^2$ 。

所以，

Arcos θ = L² − mkr 。

編排成圓錐曲線的方程式形式：

$\frac{1}{r}=\frac{mk}{L^{2}}\left(1 +\frac{A}{mk}\cos\theta\right)$ 。

離心率 e 為

$e = \frac{A}{mk} = \frac{\left|\mathbf{A}\right|}{m k}$ 。

克卜勒軌道與能量的關係可以由 LRL 向量導引出。$\mathbf{A}$ 與自己的內積為

$\begin{align} \mathbf{A}\cdot\mathbf{A} & =(\mathbf{p}\times\mathbf{L} - mk\mathbf{\hat{r}})\cdot(\mathbf{p}\times\mathbf{L} - mk\mathbf{\hat{r}}) \\ & =p^2 L^2+m^2k^2 - 2mk\hat{\mathbf{r}}\cdot(\mathbf{p}\times\mathbf{L}) \\ & =\left(2mE+\frac{2mk}{r}\right)L^2+m^2k^2 - \frac{2mk}{r}L^2 \\ \end{align}$ 。

所以，

A² = m²k² + 2mEL² 。

稍微編排，離心率的平方 e² 是能量 E 的函數：

$e^{2}=1+\frac{2L^{2}}{mk^{2}}E$ 。

假若能量 E 是負值的（束縛軌道），則離心率小於 1 ，這軌道是橢圓形軌道。相反地，假若能量是正值的（非束縛軌道，又稱為散射軌道）則離心率大於 1 ，這軌道是雙曲線軌道。最後，假若能量等於零，則離心率等於 1 ，這軌道是拋物線軌道。對於所有狀況， LRL 向量與圓錐曲線的對稱軸平行，而且從力中心點指向近拱點。

圓形的速端曲線

圖 3 :在平方反比連心力作用下，隨著粒子的軌道運動，使用速端曲線圖，固定動量向量 $\mathbf{p}$ (藍色表示) 的尾部於原點，則其頭部呈圓形移動。四個標記的點對應於圖 1 的四點。圓形的中心是在 p_y-軸，p_y-座標為 A / L （以品紅色表示），半徑是 mk / L （以綠色表示）。

假設一個粒子在做軌道運動。其速度向量的物理行為可以用速端曲線顯示出來，而動量是速度乘以質量。所以，速端曲線也可以顯示出動量的物理行為。在平方反比連心力作用下，速端曲線（圖 3 ）顯示出，粒子的動量向量的頭部呈圓形移動；這事實可以用 LRL 向量 $\mathbf{A}$ 與角動量 $\mathbf{L}$ 的保守性來證明。計算 $\mathbf{L}$ 與 $\mathbf{A}$ 的叉積：

$L^{2} \mathbf{p} = \mathbf{L} \times \mathbf{A} - mk \hat{\mathbf{r}} \times \mathbf{L}$ 。

設定 xyz 參考系的圓點在力中心點，$\mathbf{L}$ 與 z-軸同方向，x-軸與半長軸同軸。則

$p_{x}^{2} + \left(p_{y} - A/L \right)^{2} = \left( mk/L \right)^{2}$ 。

換句話說，動量 $\mathbf{p}$ 的頭部被限制於一個圓圈；圓圈的半徑為 mk / L ，圓心為 $(0,\ A/L)$ 。如圖 3 所示，圓形的動量速端曲線 毫無疑問地顯示出克卜勒問題的對稱性。

夾角 η 的一邊是點 2 與圓心的連線，另一邊是負 p_y-軸。很顯然地，離心率等於 cos η 。為了簡化運算，我們在這裏提出一個很有用的變量 $p_{0} = \sqrt{2m\left| E \right|}$ 。

運動常數與超級可積分性

在克卜勒問題裏，兩個向量 $\mathbf{A}$ ，$\mathbf{L}$ 與一個純量 E 加起來一共有七個常數純量。它們之間的相依性表達於 $\mathbf{A}\cdot\mathbf{L}=0$ 與 A² = m²k² + 2mEL² 這兩個公式。因為 $\mathbf{A}$ 的大小可以由角動量 $\mathbf{L}$ 與能量 E 計算出來。再者，$\mathbf{A}$ 必須垂直於 $\mathbf{L}$ 。所以，$\mathbf{A}$ 只能貢獻 1 個運動常數。

由於有上述兩個關係公式，這物理系統一共有五個獨立的運動常數。這結果與設定粒子軌道所需的六個初始條件（粒子的初始位置向量與初始速度向量，每一個向量有三個分量）相符合，原因是運動常數不涉及初始時間（視六個初始條件函數的參數為自變量初始時間。用其中的一個初始條件函數除去這自變量；將此初始條件函數當作一個自變量，則剰餘五個初始條件函數，函數的參數為新自變量）。

因為運動方程式是二階微分方程，一個擁有 d 自由度的物理系統，需要 2d 個初始條件來設定解答。由於運動常數不涉及初始時間，這物理系統最多只能擁有 2d − 1 個運動常數。一個擁有超過 d 個運動常數的物理系統稱為超級可積分系統；而一個擁有 2d − 1 個運動常數的物理系統稱為最大超級可積分系統。哈密頓-亞可比方程式的解答，採用任意一種坐標系統，最多只能求得 d 個運動常數。

克卜勒問題擁有三個自由度（ d = 3 ）與五個運動常數；克卜勒問題的系統是最大超級可積分系統；採用球坐標或拋物線坐標，哈密頓－亞可比方程式都是可積分的；這論據，稍後會有詳細的解釋。最大超級可積分系統可以用對易關係來量子化，這論據，稍後也會又更明瞭的說明。

在微擾勢下的系統演化

图5：橢圓軌道的慢進動，離心率 e = 0.667 。 假若，引性的連心力與平方反比定律稍微有點不同，類似的進動就會發生。

只有在一個標準的平方反比連心力下，粒子的 LRL 向量 $\mathbf{A}$ 是保守的。對於大多數的實際問題，例如行星運動，作用力並不會完全地遵守平方反比定律，而可能會含有別種微擾的連心力；稱其負值不定積分為微擾勢，標記為 h(r) 。在這種狀況下，LRL 向量會緩慢地轉動於軌道平面，相應於軌道的慢進動。假若微擾勢 h(r) 為一個保守的連心勢，也就是說，總能量 E 與角動量 $\mathbf{L}$ 都是保守的，則粒子的運動 仍舊包含於一個垂直於 $\mathbf{L}$ 的平面，大小 A 仍舊是保守的。微擾勢 h(r) 可以是任何形式的函數。但是，微擾值應該顯著地弱於主連心勢。一個典形的微擾勢可以表示為

$h(r)=-\ \frac{h}{r^n}$ ；

其中，h 是微擾勢強度，整數 $n\le 2$ 。

用正則微擾理論與作用量-角度座標，可以直接地導引出 LRL 向量的轉動率是

$\begin{align} \bar{\Omega}=\frac{\partial}{\partial L} \langle h(r) \rangle & = \frac{\partial}{\partial L} \left\{ \frac{1}{T} \int_{0}^{T} h(r) \, \mathrm{d}t \right\} \\ & = \frac{\partial}{\partial L}\left\{ \frac{m}{TL} \int_{0}^{2\pi} r^{2} h(r) \, \mathrm{d}\theta \right\} \\ \end{align}$ ；

其中，T 是軌道週期，恆等式 Ldt = mr²dθ 轉變時間積分為角積分（如圖 5 ）。角括號表達式 $\langle h(r)\rangle$ 是週期平均微擾勢；也就是說，物體繞軌道一個公轉 的平均微擾勢。取平均值可以減少轉動率的變動。

這方法曾經被用來證實愛因斯坦的廣義相對論。廣義相對論在常見的牛頓萬有引力項目外，又添加了一項小的反立方微擾 。

$h(r) = \frac{kL^{2}}{m^{2}c^{2}} \left( \frac{1}{r^{3}} \right)$ 。

將此函數代入積分。再代入 r 與 θ 的關係公式

$\frac{1}{r} =\frac{mk}{L^{2}}\left(1+\frac{A}{mk}\cos\theta\right)$ ，

就可以計算出這非牛頓微擾所產生的近拱點進動率:

$\bar{\Omega}=\frac{6\pi k^{2}}{TL^{2}c^{2}}$ 。

計算出的答案準確地符合實驗觀測到的水星進動數據和雙重脈衝星數據。這與實驗數據一致的結果被認為是廣義相對論的強證 。

帕松括號

角動量 $\mathbf{L}$ 的三個分量 L_i 的帕松括號是

$\{ L_{i}, L_{j}\} = \sum_{s=1}^{3} \epsilon_{ijs} L_{s}$ ；

其中，指標 $i,\ j=1,\ 2,\ 3$ 代表直角座標系的三個座標 $(x,\ y,\ z)$ ，$\epsilon_{ijs}$ 是列維-奇維塔符號；在這裏，為了避免與力強度的標記 k 發生混淆，採用 s 為連加運算的指標。

定義一個與 LRL 向量成比例的向量 $\mathbf{D}$ 為

$\mathbf{D}=\frac{\mathbf{A}}{\sqrt{2m\left|E\right|}}$ 。

向量 $\mathbf{D}$ 與角動量 $\mathbf{L}$ 的單位相同。$\mathbf{D}$ 與 $\mathbf{L}$ 的帕松括號為

$\{ D_{i}, L_{j}\} = \sum_{s=1}^{3} \epsilon_{ijs} D_{s}$ 。

向量 $\mathbf{D}$ 與自己的帕松括號相依於總能量 E 的正負號；也就是說，相依於是否總能量 E 是正值（在平方反比連心力作用下，產生開放的雙曲線軌道），或負值（在平方反比連心力作用下，產生閉合地橢圓軌道）。假若總能量 E 是正值，帕松括號是

$\{ D_{i}, D_{j}\} = -\sum_{s=1}^{3} \epsilon_{ijs} L_{s}$ 。

反之，假若總能量 E 是負值，帕松括號是

$\{ D_{i}, D_{j}\} = \sum_{s=1}^{3} \epsilon_{ijs} L_{s}$ 。

由於以下這三個帕松括號方程式，

$\{ L_{i}, L_{j}\} = \sum_{s=1}^{3} \epsilon_{ijs} L_{s}$ ，

$\{ D_{i}, L_{j}\}= \sum_{s=1}^{3} \epsilon_{ijs} D_{s}$ ，

$\{ D_{i}, D_{j}\} = \sum_{s=1}^{3} \epsilon_{ijs} L_{s}$ ，

我們可以確定，如果總能量 E 是負值，則克卜勒問題的對稱群是四維的旋轉群 SO(4) 。

假若總能量 E 是負值，卡西米爾不變量 $C_1,\ C_2$ 定義為

$C_{1} = \mathbf{D} \cdot \mathbf{D} + \mathbf{L} \cdot \mathbf{L} = \frac{mk^{2}}{2\left|E\right|}$ ，

$C_{2} = \mathbf{D} \cdot \mathbf{L} = 0$ 。

而且，卡西米爾不變量與 $\mathbf{D}$ 的每一個分量的帕松括號皆為零：

{C₁,D_i} = {C₂,D_i} = 0 。

還有，卡西米爾不變量與 $\mathbf{L}$ 的每一個分量的帕松括號皆為零：

{C₁,L_i} = {C₂,L_i} = 0 。

既然兩個向量 $\mathbf{D}$ 與 $\mathbf{L}$ 永遠是互相垂直的，C₂ 明顯地是零。可是，另外一個不變量 C₁ 只相依於質量 m ，力強度 k ，與總能量 E 。不變量 C₁ 分別與 D_i ，L_i 的帕松括號等於零的導引並不明顯。這不變量 C₁ ，讓我們只需用到量子力學的正則對易關係，就可以導引出類氫原子的原子能級，而不必用到的薛丁格方程式。

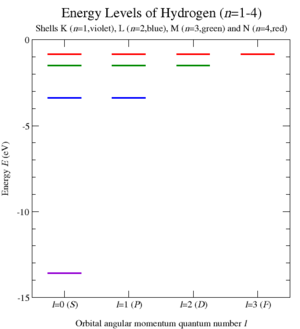
氫原子量子力學

圖 6 ：從 LRL 向量算符與角動量算符的對易關係，預測出來的氫原子的原子能級。各種實驗都準確地證實這些能級正確無誤。

帕松括號提供了一個簡易的方法來正則量子化經典系統。兩個量子算符的對易關係等於 $i\hbar$ 乘以對應的經典變量。經過這量子化程序，計算克卜勒問題的卡西米爾算符 C₁ 的本徵值 ，沃爾夫岡·包利成功地導引出類氫原子的原子能級（參閱圖 6 ），以及其發射光譜。早在薛丁格方程式成立之前，包利就研究出這重要的結果！

LRL 向量 $\mathbf{A}$ 的量子算符有一個奧妙之處，那就是動量算符與角動量算符並不對易。動量與角動量的叉積必須仔細地加以定義。LRL 向量的直角座標分量典型地定義為

$A_{k}\equiv - m_e \alpha \hat{r}_{k} + \frac{1}{2} \sum_{i=1}^{3} \sum_{j=1}^{3} \epsilon_{ijk} \left( p_{i} l_{j} + l_{j} p_{i} \right)$ ；

其中，m_e 是電子的質量，常數 $\alpha=\frac{e^2}{4\pi\epsilon_0}$ ，e 是單位電荷量，ε₀ 是真空電容率。

這定義有一個特性：指標 $i,\ j$ 是對稱的，指標 $i,\ j$ 的互換不會改變 A_k 的數值。表示為向量形式，

$\mathbf{A}=- m_e \alpha \hat{r}+\frac{1}{2}(\mathbf{p}\times\mathbf{L} - \mathbf{L}\times\mathbf{p})$ 。

那麼，其對應的哈密頓算符是

$H=\frac{\mathbf{p}^2}{2m_e} - \frac{\alpha }{r}$ 。

與 $\mathbf{A}$ 向量成正比的 $\mathbf{D}$ 向量則是

$\mathbf{D}=\frac{\mathbf{A}}{\sqrt{ - 2m_eH}}$ 。

請注意，由於哈密頓算符的本徵值是負值，所以公式內的平方根是個實數。

經過一番繁冗的運算，可以求得對易關係：

$\{L_{i},\,L_{j}\} = i\hbar\epsilon_{ijk} L_{k}$ 、

$\{L_{i},\,D_{j}\} = i\hbar\epsilon_{ijk} D_{k}$ 、

$\{D_{i},\,D_{j}\} = i\hbar\epsilon_{ijk} L_{k}$ 、

$\{H,\,D_{i}\} =0$ 。

定義第一階張量算符為

$J_{0}\equiv D_3$ 、

$J_{\pm 1}\equiv \mp \frac{1}{\sqrt{2}} \left( D_{1} \pm i D_{2} \right)$ 。

一個歸一化的第一卡西米爾算符可以同樣地定義為

$C_1\equiv \mathbf{D}^2+\mathbf{L}^2=\frac{m_e\alpha^2}{ - 2H} - \hbar^2$ 。

注意到 J _{+ 1} 和 J _{− 1} 的對易關係是

$\{J_{+1},J_{ - 1}\}=i\{D_{1},\,D_{2}\} = -\hbar L_{3}$ 。

應用維格納-艾卡定理 (Wigner-Eckart theorem) ，

$J_0|l,\,m\rangle =i\sqrt{l^2 - m^2}\ \mathfrak{C}_l|l - 1,\,m\rangle - i\sqrt{(l+1)^2 - m^2}\ \mathfrak{C}_{l+1}|l+1,\,m\rangle$ 、

$J_{+1}|l,\,m\rangle = - i\sqrt{(l - m)(l - m - 1)/2}\ \mathfrak{C}_l|l - 1,\,m+1\rangle - i\sqrt{(l+m+1)(l+m+2)/2}\ \mathfrak{C}_{l+1}|l+1,\,m+1\rangle$ 、

$J_{ - 1}|l,\,m\rangle = - i\sqrt{(l+m)(l+m - 1)/2}\ \mathfrak{C}_l|l - 1,\,m - 1\rangle - i\sqrt{(l - m+1)(l - m+2)/2}\ \mathfrak{C}_{l+1}|l+1,\,m - 1\rangle$ ；

其中，$|l,\,m\rangle$ 是角量子數為 l 、磁量子數為 l 的本徵態，$\mathfrak{C}_l$ 是常數係數。

經過一番運算， J _{+ 1} 和 J _{− 1} 的對易算符作用於 $|l,\,m\rangle$ 的結果是

$\begin{align}\{J_{+1},\,J_{ - 1}\}|l,\,m\rangle & = - m[(2l-1)\mathfrak{C}_l^2-(2l+3)\mathfrak{C}_{l+1}^2]|l,\,m\rangle \\ & = - \hbar L_3|l,\,m\rangle= - m\hbar^2 \\ \end{align}$。

所以，$\mathfrak{C}_l$ 的遞迴關係是

$(2l - 1)\mathfrak{C}_l^2 - (2l+3)\mathfrak{C}_{l+1}^2= \hbar^2$ 。

假設 $\mathfrak{C}_l^2$ 是非負值，則為了滿足上述公式，l > 0 。再假設 l 的最大值是 l_max 。由於態向量 $|l_{max}+1,\,\ \rangle$ 不存在，$\mathfrak{C}_{l_{max}+1}=0$ 。因此，$\mathfrak{C}_{l_{max}}=\frac{\hbar^2}{2l_{max} - 1}$ 。設定 n = l_max − 1 ，稍加計算，$\mathfrak{C}_l$ 的一般方程式為

$\mathfrak{C}_l=\sqrt{\frac{n^2 - l^2}{4l^2 - 1}}\ \hbar$ 。

我們會發覺原來這個 n 就是跟能級有關的主量子數。讓我們先計算 D² ：

$\begin{align}D^2|n,\,l,\,m\rangle & =[J_{+1}J_{ - 1}+J_{ - 1}J_{+1}+J_0^2]|n,\,l,\,m\rangle \\ & =(n^2 - l^2 - l - 1)\hbar^2|n,\,l,\,m\rangle \\ \end{align}$ 。

所以，第一卡西米爾算符 C₁ 作用於態向量 $|n,\,l,\,m\rangle$ 可以得到

$C_1|n,\,l,\,m\rangle=(D^2+L^2)|n,\,l,\,m\rangle=(n^2 - 1)\hbar^2|n,\,l,\,m\rangle$ 。

第一卡西米爾算符 C₁ 的本徵值是 $(n^2 - 1)\hbar^2$ 。重點是，這些本徵值不相依於量子數 l 與 m ，這造成了原子能階的簡併 ：

$E_{n} = - \frac{m_e \alpha^{2}}{2\hbar^{2} n^{2}}= - \frac{m_e e^4}{2n^2(4\pi\epsilon_0)^2\hbar^2}$。

這就是著名的氫原子波耳公式。

保守性與對稱性

在克卜勒問題裏，LRL 向量的保守性 對應於系統的一種微妙的對稱性。在經典力學裏，對稱性可以由連續運算顯示出來；這連續運算可以將一個軌道映射至另外一個軌道，而同時保持系統的能量不變。在量子力學裏，連續運算將同能級原子軌域混合在一起，也就是說，（簡併原子能級）。

通常，對於每一個對稱性都會存在有一個保守量。例如，連心力系統必對稱於旋轉群 SO(3) ；因而指引出角動量 $\mathbf{L}$ 的保守性。在經典力學裏，整個系統的旋轉不會影響軌道的能量。在量子力學裏，假若旋轉只混合角量子數相同的球諧函數，則系統的能量不會改變。

圖 7 ：同能量的動量的速端曲線家族。每一個圓圈都經過在p_x-軸上，同樣的兩點 $\pm p_{0} = \pm \sqrt{2m\left| E \right|}$ 。這一家族的速端曲線對應於一個家族的阿波羅尼奧斯圓，和雙極坐標的 σ 坐標曲面。

平方反比連心力系統的對稱性是更高維與更微妙的。這奇特的對稱性是由角動量 $\mathbf{L}$ 與 LRL 向量 $\mathbf{A}$ 的雙重保守性造成的；這保證了氫原子的能級不相依於角量子數 l 與磁量子數 m 。由於對稱性運算必須發生於更高維空間，使得這對稱性更加的微妙；這類的對稱性常稱為隱祕對稱性。在經典力學裏，克卜勒問題的高維對稱性 容許連續的改變軌道．只要保持能量不變，而角動量可以改變；換句話說，同能量，不同角動量（離心率）的軌道可以互相的連續變換。在量子力學裏，這對應著不同角量子數 l 與磁量子數 m 的軌域的混合，例如 s(l = 0) 與 p(l = 1) 原子軌域的混合。這種混合是不能用普通的三維平移運算或旋轉運算達成的。可是，這種混合等價於高維度空間的旋轉。

在一個束縛 (bounded) 系統裏，能量是負值的，這高維對稱群是 SO(4) ；特性是四維向量的長度保持不變：

$\left| \mathbf{e} \right|^2=e_1^2+e_2^2+e_3^2+e_4^2$ 。

1935 年，弗拉基米爾·佛克 (Vladimir Fock)表明，在量子力學裏，束縛的克卜勒問題 等價於 一個粒子自由地移動於 四維空間的三維單位球。更具體地，佛克表明，在克卜勒問題的動量空間，薛丁格波函數是球諧函數的球極平面投影。圓球的旋轉與重複射影造成了橢圓軌域的連續映射，同時維持能量不變；這對應於主量子數 n 相同的軌域的混合。隨後，華倫泰·巴格曼注意到，跟 LRL 向量成比例的向量 $\mathbf{D}$ 與角動量 $\mathbf{L}$ 的帕松括號形成 SO(4) 的李代數。簡單地說，$\mathbf{D}$ 與 $\mathbf{L}$ 的六個物理量對應於在四維空間裏的六個保守的角動量分量，相伴於在四維空間裏的六個合法的簡單旋轉（從四個軸中，選兩個軸為旋轉軸。一共有六種可能）。這結論並不意示我們的宇宙是一個三維球面；而只是說，這個特別的物理問題（克卜勒問題），在數學上，等價於移動於三維球面的一個自由粒子。

在一個非束縛 (unbound) ，散射系統裏，能量是正值的，對應的高維對稱群是 SO(3,1) ；其特性是保持四維矢量的閔考斯基長度不變：

$ds^{2} = e_{1}^{2} + e_{2}^{2} + e_{3}^{2} - e_{4}^{2}$ 。

連心力系統（包括克卜勒問題的那些系統）的軌道對於反射也具有對稱性。所以，軌道的完全對稱群並不是前面所提的 SO(3) 、SO(4) 、SO(3,1) 群；而分別是 O(3) 、O(4) 、O(3,1) 。然而，我們只需要連通子群 SO(3) 、SO(4) 、SO(3,1) 來展示出角動量與 LRL 向量的保守性；反射對稱性與保守性不相關。保守性可以由群的李代數導引出來。

旋轉對稱性在四維空間

圖 8 ：圖 7 的動量的速端曲線對應於 η 三維單位球的大圓線的球極平面投影。每一個大圓線都與 η_x-軸相交，後者垂直於頁面。投影是從北極（ w 單位向量）到 η_xη_x-平面，如同這裏的虛黑線表示於品紅色速端曲線。在緯度 α 的大圓線對應於離心率 $e=sin\ \alpha$ 。在這圖裏的大圓線的顏色對應於它們在圖 7 的速端曲線。

克卜勒問題與四維旋轉對稱性 SO(4) 的關聯可以很容易地觀察出來。標記四維直角座標為 $(w,\ x,\ y,\ z)$ ；其中， $(x,\ y,\ z)$ 代表三維位置向量 $\mathbf{r}$ 的直角座標。三維動量 $\mathbf{p}$ 與三維單位球的四維向量 $\boldsymbol\eta$ 的關係為

$\boldsymbol\eta =\displaystyle \frac{p^{2} - p_{0}^{2}}{p^{2} + p_{0}^{2}} \mathbf{\hat{w}} + \frac{2 p_{0}}{p^{2} + p_{0}^{2}} \mathbf{p}$ ；

其中， $\mathbf{\hat{w}}$ 是新的 w-軸的單位向量。

很簡單地，我們可以核對 $\boldsymbol\eta$ 也是一個單位向量：

$\boldsymbol\eta=\hat{\boldsymbol\eta}$ 。

從 $\mathbf{p}$ 至 $\hat{\boldsymbol\eta}$ 的映射有一個獨特唯一的逆反；例如，動量 $\mathbf{p}$ 的 x-軸分量是

$p_{x} = p_{0} \frac{\eta_{x}}{1 - \eta_{w}}$。

p_y 與 p_z 也有類似的公式。換句話說，三維動量向量 $\mathbf{p}$ 是四維單位向量 $\hat{\boldsymbol\eta}$ 的球極平面投影，其比例因子為 p₀ 。

選擇一個合適的直角座標，使 z-軸與角動量 $\mathbf{L}$ 同直線，使動量的速端曲線的取向如同圖 7 ，圓心包含於 y-軸。這樣，不失廣義性，我們可以觀察到這旋轉對稱性。由於粒子的運動包含於一個平面，$\mathbf{p}$ 與 $\mathbf{L}$ 互相垂直，而且，p_z = η_z = 0 。因此，我們只需要專注於三維向量 $\hat{\boldsymbol\eta}=(\eta_w,\ \eta_x,\ \eta_y)$ 。圖 7 速端曲線的阿波羅尼奧斯圓 家族對應於在三維單位球 $\boldsymbol\eta$ 的大圓線家族。每一個大圓線與 η_x 相交於兩個交點 $\eta_x=\pm 1$ 。這兩個交點相對於速端曲線圖的兩點 $p_x=\pm p_0$ 。這兩個交點也是這些大圓線的共同交點。所以，這些大圓線的互相關係是一個環繞著 η_x-軸的簡單旋轉（參閱圖 8 ）。以 η_x-軸為轉軸，每一個大圓線的位置是從 η_xη_y-平面旋轉 α 角。

取任意一個大圓線 η_y 最大值的一點，其坐標為 $(\eta_w,\ 0,\ \eta_y,\ 0)$ 。那麼，

p_x = 0 、

p_y = p = (A + mk) / L 、

$\eta_y=cos(\alpha)=\frac{2p_0 p_y}{p_y^2+p_0^2}$ 。

經過一番運算，代入 p₀ 的值，可以得到

$\begin{align} sin(\alpha) & =\frac{p_y^2 - p_0^2}{p_y^2+p_0^2} \\ & =\frac{(A+mk)^2 - 2m|E|L^2}{(A+mk)^2+2m|E|L^2} \\ \end{align}$ 。

給予一個束縛軌道，能量是負值的：

$\begin{align} sin(\alpha) & =\frac{(A+mk)^2+2mEL^2}{(A+mk)^2 - 2mEL^2} \\ & =\frac{A}{mk}=e \\ \end{align}$ 。

所以，離心率 e = sin(α) 是緯度 α 的正弦函數。

由於圖 7 的動量的速端曲線對應於 η 三維單位球的大圓線的球極平面投影，而這速端曲線家族的成員都擁有相同的能量。所以，這旋轉的對稱性使所有能量相同的軌道都能夠互相變換。但是，這旋轉正交於通常的三維旋轉，因為它涉及了第四維 η_w 。高維度的對稱性是克卜勒問題對應於 LRL 向量的一個特徵。

採用橢圓柱坐標 $\chi,\ \psi,\ \phi$ 來代替四維座標 $\boldsymbol\eta$ ，克卜勒問題有一個精緻的作用量-角度座標解答：

$\eta_{w} = \mathrm{cn}\, \chi \ \mathrm{cn}\, \psi$ ，

$\eta_{x} = \mathrm{sn}\, \chi \ \mathrm{dn}\, \psi \ \cos \phi$ ，

$\eta_{y} = \mathrm{sn}\, \chi \ \mathrm{dn}\, \psi \ \sin \phi$ ，

$\eta_{z} = \mathrm{dn}\, \chi \ \mathrm{sn}\, \psi$ ；

其中， $\mathrm{sn},\,\mathrm{cn},\,\mathrm{dn}$ 是亞可比橢圓函數。

克卜勒問題 LRL 向量恆定的證明

以下幾種導引可以推導出，在平方反比連心力下，LRL 向量守恆。

直接證明

假設，一個連心力 $f(\mathbf{r})\hat{\mathbf{r}}$ 作用於一個粒子。根據牛頓第二定律，運動方程式為

$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=f(\mathbf{r}) \hat{\mathbf{r}}$ ；

其中，$f(\mathbf{r})$ 是函數，$\mathbf{r}$ 為粒子的位置，$\mathbf{p}$ 是動量，t 是時間。

由於在連心力下，角動量 $\mathbf{L} = \mathbf{r} \times \mathbf{p}$ 是恆定的，

$\frac{\mathrm{d}}{\mathrm{d}t}\mathbf{L} = 0$ 。

所以，

$\frac{\mathrm{d}}{\mathrm{d}t}\left( \mathbf{p}\times\mathbf{L} \right)=\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} \times \mathbf{L} = f(\mathbf{r}) \mathbf{\hat{r}} \times \left( \mathbf{r} \times m \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right) = f(\mathbf{r}) \frac{m}{r} \left[ \mathbf{r} \left(\mathbf{r} \cdot \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right) - r^{2} \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right]$ 。

代入以下恆等式：

$\mathbf{r}\cdot\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}=\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}\left(\mathbf{r}\cdot\mathbf{r}\right) =\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}\left(r^{2}\right)=r\frac{\mathrm{d}r}{\mathrm{d}t}$，

可以得到方程式，

$\frac{\mathrm{d}}{\mathrm{d}t} \left( \mathbf{p} \times \mathbf{L} \right) = - m f(\mathbf{r}) r^{2} \left[ \frac{1}{r} \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} - \frac{\mathbf{r}}{r^{2}} \frac{\mathrm{d}r}{\mathrm{d}t}\right] = - m f(\mathbf{r}) r^{2} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\mathbf{r}}{r}\right)$ 。

代入平方反比連心力的方程式 $f(\mathbf{r})=\frac{ - k}{r^{2}}$ ，

$\frac{\mathrm{d}}{\mathrm{d}t} \left( \mathbf{p} \times \mathbf{L} \right) = m k \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\mathbf{r}}{r}\right) = \frac{\mathrm{d}}{\mathrm{d}t} \left( mk\mathbf{\hat{r}} \right)$ 。

所以，在平方反比連心力下，$\mathbf{A}$ 是恆定的：

$\frac{\mathrm{d}}{\mathrm{d}t} \mathbf{A} = \frac{\mathrm{d}}{\mathrm{d}t} \left( \mathbf{p} \times \mathbf{L} \right) - \frac{\mathrm{d}}{\mathrm{d}t} \left( mk\mathbf{\hat{r}} \right) = 0$ 。

哈密頓-亞可比方程式

我們也可以用哈密頓-亞可比方程式的可分性導引出 LRL 向量的恆定性。採用拋物線座標 $(\xi,\ \eta)$ ，定義

ξ = r + x 、

η = r − x ；

其中，$(x,\ y)$ 是直角座標，r 是軌道的徑向距離：

$r = \sqrt{x^{2} + y^{2}}$ 。

逆反過來，

$x = \frac{1}{2} \left( \xi - \eta \right)$ 、

$y = \sqrt{\xi\eta}$ 。

則克卜勒問題的哈密頓量為

$\begin{align}H & = \frac{1}{2}m\dot{x}^2+\frac{1}{2}m\dot{y}^2-\frac{k}{r} \\ & =\frac{2\xi p_{\xi}^2}{m(\xi+\eta)}+\frac{2\eta p_{\eta}^2}{m(\xi+\eta)} - \frac{2k}{\xi+\eta} \\ \end{align}$ ；

其中，$p_{\xi},\ p_{\eta}$ 分別是廣義座標 $\xi,\ \eta$ 的共軛動量。

由於克卜勒問題的勢函數只相依於廣義座標，哈密頓量是個能量運動常數，H = E 。稍加編排，可以得到

$2\xi p_{\xi}^2 - mk - mE\xi= - 2\eta p_{\eta}^2+mk+mE\eta$ 。

這公式的左手邊與右手邊分別相依於不同的廣義座標，所以，兩邊都相等於一個運動常數，標記為 Γ ：

$2\xi p_{\xi}^{2} - mk - mE\xi = - \Gamma$ 、

$2\eta p_{\eta}^{2} - mk - mE\eta = \Gamma$ 。

思考 LRL 向量的 x 分量，

$\begin{align} A_{x} & = p_{y}(xp_{y} - yp_{x}) - mk\frac{x}{r} \\ & = xp_{y}^2 - yp_{x}p_y - mk+m\eta\frac{k}{r} \\ \end{align}$ 。

代入能量方程式 $E=\frac{1}{2}mv^2 - \frac{k}{r}$ ，則

$A_{x}=xp_{y}^2 - yp_{x}p_y+\frac{1}{2}m^2 v^2 \eta - mk - mE\eta$ 。

這公式右手邊，前三個項目，經過一番計算，可以得到

$xp_{y}^2 - yp_{x}p_y+\frac{1}{2}m^2 v^2 \eta =\frac{m^2}{8}\dot{\eta}^2\frac{(\eta+\xi)^2}{\eta}=2\eta p_{\eta}^2$ 。

所以，A_x 也是運動常數：

A_x = Γ 。

諾特定理

LRL 向量的保守性與前面所提的旋轉對稱性，兩者之間的關係，可以用諾特定理來做連結分析。諾特定理也可以用來辨明 LRL 向量是運動常數。諾特定理表明：在一個物理系統裏，對於廣義坐標 q_i 的微小變分 $\delta q_{i} = \epsilon g_{i}(\mathbf{q},\ \mathbf{\dot{q}},\ t)$ ，假若，取至微小參數 $\epsilon$ 的一階，拉格朗日量 $\mathcal{L}$ 的變分 $\delta \mathcal{L}$ 是

$\delta \mathcal{L} = \epsilon \frac{\mathrm{d}}{\mathrm{d}t} G(\mathbf{q},\ t)$ ，

則必存在保守量 Γ 滿足方程式

$\Gamma = - G+\sum_{i}g_i\left(\frac{\partial \mathcal{L}}{\partial\dot{q}_i}\right)$ ；

其中，$g_i(\mathbf{q},\ \mathbf{\dot{q}},\ t)$ 、 $G(\mathbf{q},\ t)$ 都是函數。

更具體地，在一個克卜勒問題裏，試設定坐標 x_i 的微小變分為

$\delta x_i=\frac{\epsilon}{2} \left[ 2p_{i}x_{s} - x_{i}p_{s} - (\mathbf{r}\cdot \mathbf{p})\delta_{is} \right]$ ；

其中，$i=1,\ 2,\ 3$ ，x_i 與 p_i 分別為位置 $\mathbf{r}$ 與動量 $\mathbf{p}$ 的 i-軸分量，δ_is 是克羅內克爾δ，s 是固定的下標。

由於克卜勒問題的拉格朗日量是

$\mathcal{L}=\sum_{i}\left(\frac{1}{2}m\dot{x}_i\dot{x}_i\right)+\frac{k}{r}$ 。

其運動方程式為

$m\ddot{x}_i+k\frac{x_i}{r^3}=0$ 。

對應於坐標 x_i 的變分，速度 $\dot{x}_{i}$ 的變分為

$\begin{align} \delta \dot{x}_{i} & = \frac{\epsilon}{2} \left[2\dot{p}_{i} x_{s}-x_{i}\dot{p}_{s}+p_{i}\dot{x}_{s} - \frac{p^2}{m}\delta_{is} - (\mathbf{r}\cdot\dot{\mathbf{p}})\delta_{is} \right] \\ & = \frac{\epsilon}{2} \left[ - \frac{k}{r^3}x_i x_s+p_{i}\dot{x}_{s} - \frac{p^2}{m}\delta_{is} +\frac{k}{r}\delta_{is} \right] \\ \end{align}$。

拉格朗日量取至一階的變分是

$\begin{align} \delta \mathcal{L} & =\sum_{i}\left(\frac{\partial \mathcal{L}}{\partial x_i}\delta x_i + \frac{\partial \mathcal{L}}{\partial \dot{x}_i}\delta \dot{x}_i\right) \\ & =\sum_{i}\left( - \frac{kx_i}{r^3}\delta x_i+m\dot{x}_i\delta\dot{x}_i\right) \\ \end{align}$。

代入 δx_i 和 $\delta\dot{x}_i$ 的公式，經過一番繁瑣的運算，可以得到

$\delta\mathcal{L}=\epsilon mk\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{x_{s}}{r} \right)$ 。

再代入保守量 Γ 的公式，則會得到

$\Gamma=p^{2} x_{s} - p_{s}\left(\mathbf{r} \cdot \mathbf{p}\right) - \frac{mkx_{s}}{r}=\left[\mathbf{p}\times \mathbf{L} - mk\hat{\mathbf{r}}\right]_{s}$ ；

而這正是 LRL 向量的 s-軸分量 A_s 。

李變換

圖 9: 導引出 LRL 向量保守性的李變換。當這比例參數 λ 改變時，能量與角動量的大小也一起改變，可是離心率 e 與 LRL 向量 $\mathbf{A}$ 的大小與方向不變。

諾特定理精緻地導引出 LRL 向量的保守性。美中不足地，這導引有一個弱點：坐標變分δx_i 不只涉及了位置 $\mathbf{r}$ ，而且還涉及了動量 $\mathbf{p}$ 。假若，我們使用數學家索菲斯·李創建的方法來導引，可以除去這弱點 。具體地，我們可以定義一個李變換，座標 $\mathbf{r}$ 與時間 t 都按照比例變換，比例是參數 λ 的不同羃數：

$t \rightarrow \lambda^{3}t, \ \mathbf{r} \rightarrow \lambda^{2}\mathbf{r}, \ \mathbf{p} \rightarrow \frac{1}{\lambda}\mathbf{p}$ 。

這變換改變了角動量 L 的大小與能量 E ：

$L \rightarrow \lambda L, \ E \rightarrow \frac{1}{\lambda^{2}} E$ 。

可是，仍舊保持乘積 EL² 不變。所以，離心率 e 與 LRL 向量 $\mathbf{A}$ 的大小不變。這可以從 A² 的公式觀察出：

A² = m²k²e² = m²k² + 2mEL² 。

由於半短軸與半長軸的取向 不因整體的比例變換 而改變，LRL 向量 $\mathbf{A}$ 的方向也會保持不變。在李變換下，克卜勒第三定律也仍舊成立：半長軸 a 與週期 T 形成常數T² / a³ 。

推廣至別種位勢和相對論

LRL 向量可以推廣至其他狀況；可以用來辨認在其他狀況下的保守值。

假設，一個物理系統裏，存在著電場 $\mathbf{E}$ ，保守的廣義 LRL 向量 $\mathcal{A}$ 是

$\mathcal{A} = \mathbf{A} + \frac{mq}{2} \left[ \left( \mathbf{r} \times \mathbf{E} \right) \times \mathbf{r} \right]$ ；

其中，q 是粒子的電荷量。

最廣義的 LRL 向量的形式可以表達為

$\mathcal{A}=\left( \frac{\partial \xi}{\partial u} \right) \left(\mathbf{p} \times \mathbf{L}\right)+\left[\xi - u \left( \frac{\partial \xi}{\partial u} \right)\right] L^{2} \mathbf{\hat{r}}$ ；

其中，$u=\frac{1}{r}$ （參閱伯特蘭定理），ξ = cos θ ，角 θ 定義為

$\theta = L \int^{u} \frac{du}{\sqrt{m^{2} c^{2} \left(\gamma^{2} - 1 \right) - L^{2} u^{2}}}$ ；

其中，γ 是勞侖茲因子。

如同前面所提，計算 $\mathbf{L}$ 與 $\mathcal{A}$ 的叉積，可以得到一個保守的副法線向量 $\mathcal{B}$ ：

$\mathcal{B}=\mathbf{L}\times\mathcal{A}$ 。

綜和兩個向量成為一個保守的並矢張量 $\mathcal{W}$ ：

$\mathcal{W} = \alpha \mathcal{A} \otimes \mathcal{A} + \beta \, \mathcal{B} \otimes \mathcal{B}$ 。

舉例說明，計算一個非相對論性，均向性諧振子的 LRL 向量。由於作用力是連心力，$\mathbf{F}(r)= -k \mathbf{r}$，力子的角動量是保守的，粒子的運動包含於一個平面。請注意， $\mathbf{P}$ 與 $\mathbf{L}$ 不是一定互相垂直的。保守的並矢張量可以表達為一個簡單的形式：

$\mathcal{W} = \frac{1}{2m} \mathbf{p} \otimes \mathbf{p} + \frac{k}{2} \, \mathbf{r} \otimes \mathbf{r}$ 。

其相應的 LRL 向量必較複雜

$\mathcal{A} = \frac{1}{\sqrt{mr^{2}\omega_{0} A - mr^{2}E + L^{2}}} \left\{ \left( \mathbf{p} \times \mathbf{L} \right) + \left(mr\omega_{0} A - mrE \right) \mathbf{\hat{r}} \right\}$ ；

其中， $\omega_{0} = \sqrt{\frac{k}{m}}$ 是自然振率。

別種比例與表述

不同於動量與角動量，並沒有學術界一致認同的 LRL 向量定義；在科學文獻裏，存在有幾種不同的比例因子與符號。前面所述的定義是最普遍的定義。另外一種常見的定義，將 $\mathbf{A}$ 除以常數 mk ；這樣，可以得到一個無因次的離心率向量 $\mathbf{e}$ ：

$\mathbf{e}=\frac{1}{mk} \left(\mathbf{p} \times \mathbf{L} \right) - \mathbf{\hat{r}} = \frac{m}{k} \left(\mathbf{v} \times \mathbf{L}\right) - \mathbf{\hat{r}}$ ；

其中，$\mathbf{v}$ 是速度。

離心率向量 $\mathbf{e}$ 的方向與 $\mathbf{A}$ 相同，大小是軌道的離心率。

別種比例的版本也可能會用到。例如，將 $\mathbf{A}$ 除以 m ：

$\mathbf{M} = \mathbf{v} \times \mathbf{L} - k\mathbf{\hat{r}}$，

或者，將 $\mathbf{A}$ 除以 P₀ ：

$\mathbf{D}=\frac{\mathbf{A}}{P_{0}}=\frac{1}{\sqrt{2m\left| E \right|}} \left\{ \mathbf{p} \times \mathbf{L} - m k \mathbf{\hat{r}} \right\}$ 。

$\mathbf{D}$ 與角動量 $\mathbf{L}$ 的單位相同。在非常稀有的狀況， LRL 向量的正負號會改變。這些，都不會影響它是運動常數的事實。

圖 4: 角動量 $\mathbf{L}$ ， LRL 向量 $\mathbf{A}$ ，與副法線向量 $\mathbf{B}$ 都互相垂直。$\mathbf{A}$ 與 $\mathbf{B}$ 分別和橢圓的半長軸與半短軸的指向相同。

另外一個保守的向量是副法線向量 $\mathbf{B}$ 。威廉·哈密頓曾經研究過這向量。

$\mathbf{B} = \mathbf{p} - \left(\frac{mk}{L^{2}r} \right) \ \left( \mathbf{L} \times \mathbf{r} \right)$ 。

這保守的向量與橢圓的半短軸同直線。$\mathbf{A}$ 是 $\mathbf{B}$ 叉積 $\mathbf{L}$ （參閱圖 4 ）。兩個向量 $\mathbf{A}$ 與 $\mathbf{B}$ 可以結合起來形成一個保守的並矢張量 $\mathcal{W}$ ：

$\mathcal{W} = \alpha \mathbf{A} \otimes \mathbf{A} + \beta \, \mathbf{B} \otimes \mathbf{B}$ ；

其中，α 與 β 是任意比例常數，符號 $\otimes$ 表示張量積。展開這公式為

$\mathcal{W}_{ij} = \alpha A_{i} A_{j} + \beta B_{i} B_{j}$ 。

由於兩個向量互相垂直，$\mathbf{A}$ 與 $\mathbf{B}$ 可以視為保守的張量 $\mathcal{W}$ 的主軸，也就是說，按比例的特徵向量。由於$\mathbf{A}$ 與 $\mathbf{B}$ 都垂直於 $\mathbf{L}$ ，張量 $\mathcal{W}$ 垂直於角動量 $\mathbf{L}$ ：

$\mathbf{L} \cdot \mathcal{W} = \alpha \left( \mathbf{L} \cdot \mathbf{A} \right) \mathbf{A} + \beta \left( \mathbf{L} \cdot \mathbf{B} \right) \mathbf{B} = 0$ 。

參閱

• 二體問題
• 伯特蘭定理
• 量子力學
• 航天動力學: 軌道, 離心率向量, 軌道根數

參考文獻

• Leach, P.G.L.; G.P. Flessas, Generalisations of the Laplace–Runge–Lenz vector, J. Nonlinear Math. Phys.. 2003, 10: 340–423, arXiv:math-ph/0403028 

外部連結

• 加利福尼亞大學河濱分校物理網頁：Baez, John. Mysteries of the gravitational 2-body problem.