多面形
 以六面形为例 | ||
| 类别 | 正多面体 球面镶嵌 | |
|---|---|---|
| 对偶多面体 | 多边形二面体 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
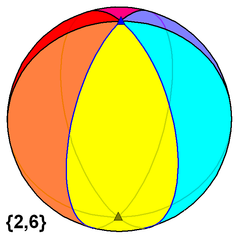
| 施莱夫利符号 | {2,n} | |
| 威佐夫符号 | n | 2 2 | |
| 性质 | ||
| 面 | ||
| 边 | ||
| 顶点 | ||
| 欧拉特征数 | F=, E=, V= (χ=2) | |
| 组成与布局 | ||
| 面的种类 | n个二角形 | |
| 顶点图 | 2n | |
| 顶点布局 | 2n | |
| 对称性 | ||
| 对称群 | Dnh, [2,n], (*22n), order 4n | |
| 旋转对称群 | Dn, [2,n]+, (22n), order 2n | |
| 图像 | ||
| ||
| 注:为底面边数 。 | ||
在几何学中,多面形(英语:Hosohedron)是一种由月牙形或球弓形组成的球面镶嵌,并且使得每一个月牙形或球弓形共用相同的两个顶点。其在施莱夫利符号中用 {2, n} 表示n面形。
其亦可以视为由球面正二角形组成的球面镶嵌图,又称为二角形镶嵌或二边形镶嵌。
正多面形
[编辑]在施莱夫利符号中以{m, n}表示的正多面体,其面的个数存在下列等式:
自古以来大家所熟知的正多面体——柏拉图立体是当m≥3且n≥3的整数解,限制在m≥3的状态下,多边形面必须至少有三条边。
当考虑多面体为球面镶嵌时,该限制可以放宽,因为二角形(二边形)可以以球弓形或月牙形存在,即球面二角形具有非零面积。当m=2时则会产生一个新的无穷集合,即多面形。在球面上,所述多面体{2, n}表示当n个球弓形组合,并且具有2π/n内角。所有二角形阶共用相同的两个顶点,即每个顶点皆为所有二角形的公共顶点。
每个正多面形都是n阶二边形镶嵌。
 一个正三面形,{2,3},以三个月牙形镶嵌于求面表示。又称三阶二边形镶嵌。 |
 一个正四面形,以四个月牙形镶嵌于求面表示。又称四阶二边形镶嵌。 |
| 球面镶嵌 | 欧式镶嵌 仿紧空间 |
双曲镶嵌 非紧空间 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ | iπ/λ |
| 一面形 | 二面形 | 三面形 | 四面形 | 五面形 | 六面形 | 七面形 | 八面形 | 九面形 | 十面形 | 十一面形 | 十二面形 | 无限面形 | 超无限面形 | |
{2,1} |
{2,2} |
{2,3} |
{2,4} |
{2,5} |
{2,6} |
{2,7} |
{2,8} |
{2,9} |
{2,10} |
{2,11} |
{2,12} |
{2,∞} |
{2,iπ/λ} | |

|

|

|

|

|

|

|

|

|

|

|

|

|

| |
命名
[编辑]英文Hosohedron一词由考克斯特命名,其来自希腊语ὅσος (osos/hosos),是‘尽可能多’的意思,其意思为‘尽可能达到很多的面的形状[1]’因此称为多面形。
多维面形
[编辑]多维面形是多面形在高维度的类比,表示有多个维面的几何图形。任何正的维面形都可以以施莱夫利符号{2,p,...,q}表示
| 施莱夫利 {2,p,q} |
考克斯特符号 |
胞 {2,p}π/q |
面 {2}π/p,π/q |
边 | 顶点 | 顶点图 {p,q} |
对称性 | 对偶多胞形 |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} | 4 {2,3}π/3 
|
6 {2}π/3,π/3 |
4 | 2 | {3,3}
|
[2,3,3] | {3,3,2} | |
| {2,4,3} | 6 {2,4}π/3 
|
12 {2}π/4,π/3 |
8 | 2 | {4,3}
|
[2,4,3] | {3,4,2} | |
| {2,3,4} | 8 {2,3}π/4 
|
12 {2}π/3,π/4 |
6 | 2 | {3,4}
|
[2,4,3] | {4,3,2} | |
| {2,5,3} | 12 {2,5}π/3 
|
30 {2}π/5,π/3 |
20 | 2 | {5,3}
|
[2,5,3] | {3,5,2} | |
| {2,3,5} | 20 {2,3}π/5 
|
30 {2}π/3,π/5 |
12 | 2 | {3,5}
|
[2,5,3] | {5,3,2} |
相关几何体
[编辑]多香肠面形
[编辑]
多香肠面形(lucanicohedron)又称为截半多面形(rectified hosohedron)是一种半正则地区图,源自于多面形,其结构为两个多边形底面以类似多边形二面体的方式贴合,但贴合的棱处加上二角形的侧面所构成的正则地区图[2],名称lucanicohedron源自于这种立体以二角形在侧面循环有如香肠串一般,因此取香肠的希腊语λουκάνικο作为字首lucanico-结合多面体字尾-hedron构成的复合词。[3]
参见
[编辑]参考文献
[编辑]- ^ Steven Schwartzman. The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. MAA. 1 January 1994: 108–109 [2014-06-19]. ISBN 978-0-88385-511-9. (原始内容存档于2014-06-26).
- ^ Draghicescu, Mircea; et al. Single-threaded Polyhedra Models. Bridges 2020 Conference Proceedings (Tessellations Publishing). 2020: 281–288 [2022-12-22]. (原始内容存档于2022-12-22).
- ^ glossary§lucanicohedron. weddslist.com. [2022-12-22]. (原始内容存档于2021-05-07).
- ^ Draghicescu, Mircea. Building Polyhedra Models for Mathematical Art Projects and Teaching Geometry (PDF). Proceedings of Bridges 2019: Mathematics, Art, Music, Architecture, Education, Culture. 2019: 629–634 [2022-12-23]. (原始内容存档 (PDF)于2022-12-23).
- Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- 埃里克·韦斯坦因. Hosohedron. MathWorld.




