在數學中,雙曲線(英語:hyperbola;希臘語:ὑπερβολή,意思是超過、超出)是定義為平面交截直角圓錐面的兩半的一類圓錐曲線。
它還可以定義為與兩個固定的點(稱為焦點)的距離差是常數的點的軌跡。這個固定的距離差是 的兩倍,這裏的
的兩倍,這裏的 是從雙曲線的中心到雙曲線最近的分支的頂點的距離。
是從雙曲線的中心到雙曲線最近的分支的頂點的距離。 還稱為雙曲線的半貫軸。焦點位於貫軸上,它們的中間點稱為中心。
還稱為雙曲線的半貫軸。焦點位於貫軸上,它們的中間點稱為中心。
從代數上說,雙曲線是在笛卡爾平面上由如下方程定義的曲線

使得 ,這裏的所有系數都是實數,並存在定義在雙曲線上的點對
,這裏的所有系數都是實數,並存在定義在雙曲線上的點對 的多於一個的解。
的多於一個的解。
在笛卡爾坐標平面上,兩個互為倒數的變量的圖像是雙曲線。
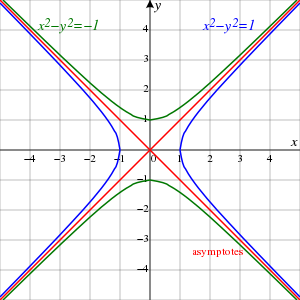 共軛單位直角雙曲線
共軛單位直角雙曲線
上面已經列出:
- 平面切直角圓錐面的兩半的交截線。
- 與兩個固定點(稱為焦點)距離差為常數的點的軌跡。
- 到一個焦點的距離和到一條直線(稱為準線)的距離的比例是大於
 的常數的點的軌跡。這個常數稱為雙曲線的離心率。
的常數的點的軌跡。這個常數稱為雙曲線的離心率。
雙曲線由分開兩個焦點的兩個分離的稱為臂或分支的曲線構成。隨着到焦點的距離的變大,雙曲線就越逼近稱為漸近線的兩條線。漸近線交叉於雙曲線的中點,並對於東西開口的雙曲線有斜率 ,對於北南開口的雙曲線有斜率
,對於北南開口的雙曲線有斜率 。
。
雙曲線有個性質,出自一個焦點的射線反射於雙曲線後看起來像是出自另一個焦點。
雙曲線的一個特殊情況是「等軸」或「直角」雙曲線,它的漸近線交於直角。以坐標軸作為漸近線的直角雙曲線由方程 給出,這裏的
給出,這裏的 是常數。
是常數。
如果對雙曲線方程交換 和
和 ,得到它的共軛雙曲線。共軛雙曲線有同樣的漸近線。
,得到它的共軛雙曲線。共軛雙曲線有同樣的漸近線。
中心位於 的左右開口的雙曲線:
的左右開口的雙曲線:

中心位於 的上下開口的雙曲線:
的上下開口的雙曲線:

貫軸貫穿雙曲線的中心並交雙曲線兩臂於它們的頂點。焦點位於雙曲線貫軸的延長線上。共軛軸貫穿雙曲線中點並垂直於貫軸。
在兩個公式中, 是半貫軸(在雙曲線兩臂之間沿着貫軸測量的距離),而
是半貫軸(在雙曲線兩臂之間沿着貫軸測量的距離),而 是半共軛軸。
是半共軛軸。
如果用雙曲線的兩個頂點的切線交漸近線形成一個矩形,在切線上的兩邊的長度是 ,平行於貫軸的兩邊的長度是
,平行於貫軸的兩邊的長度是 ,注意
,注意 可以大於
可以大於 。
。
如果計算從雙曲線上任意準線上的點到每個焦點的距離,這兩個距離的差的絕對值總是 。
。
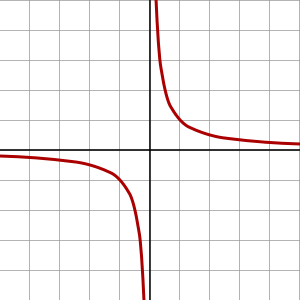 直角雙曲線
直角雙曲線 的圖像。
的圖像。
離心率給出自:

左右開口的雙曲線的焦點是: ,其中c給出自
,其中c給出自 。
。
上下開口的雙曲線的焦點是: ,其中c給出自
,其中c給出自 。
。
等軸雙曲線的貫軸與共軛軸長相等,即 且
且 ,此時漸近線方程為
,此時漸近線方程為 (無論焦點在
(無論焦點在 軸還是
軸還是 軸)。
軸)。
單位雙曲線屬於等軸雙曲線,且半貫軸和半共軛軸的長均為 ,即
,即 ,滿足方程:
,滿足方程:
 或
或 。
。
對於以直線 和直線
和直線 為漸近線的直角雙曲線:
為漸近線的直角雙曲線:

這種雙曲線最簡單的例子是:

當雙曲線 的貫軸是雙曲線
的貫軸是雙曲線 的共軛軸,且雙曲線
的共軛軸,且雙曲線 的共軛軸是雙曲線
的共軛軸是雙曲線 的貫軸時,稱雙曲線
的貫軸時,稱雙曲線 與雙曲線
與雙曲線 為共軛雙曲線。若
為共軛雙曲線。若 的方程為
的方程為

則 的方程為
的方程為

其特點為:
- 共漸近線,與漸近線平行的直線和雙曲線有且只有一個交點。
- 焦距相等。
- 兩雙曲線的離心率平方後的倒數相加等於
 。
。
左右開口的雙曲線:

上下開口的雙曲線:

上右下左開口的雙曲線:

上左下右開口的雙曲線:

在所有公式中,中心在極點,而 是半貫軸和半共軛軸。
是半貫軸和半共軛軸。
如同正弦和餘弦函數給出橢圓的參數方程,雙曲函數給出雙曲線的參數方程。
左右開口的雙曲線:

或

上下開口的雙曲線:

或

在所有公式中, 是雙曲線的中點,
是雙曲線的中點, 是半貫軸而
是半貫軸而 是半共軛軸。
是半共軛軸。
焦點在 軸:
軸:
焦點在 軸:
軸:
焦線平行於 軸:
軸:
焦線平行於 軸:
軸:

當 時,表示雙曲線。其中
時,表示雙曲線。其中 為焦點到準線距離,
為焦點到準線距離, 為弦與
為弦與 軸夾角。
軸夾角。






















































