伽羅瓦理論

数学中,特别是抽象代数理论中,得名于法國數學家埃瓦里斯特·伽罗瓦的伽罗瓦理论提供了域论和群论之间的联系,即伽罗瓦理论基本定理。这样可以将域论中的某些问题还原到群论,使其更简单、更易理解。
若方程的根可用只涉及整数、方根与4种基本算术运算的式子表示,就称方程是根式可解的。伽罗瓦将多项式的根引入为研究课题,这样能根据多项式根置换群的性质描述根式可解多项式方程的特征。这广泛地概括了阿贝尔-鲁菲尼定理,其指出五次及以上的一般多项式不是根式可解的。
伽罗瓦理论证明古典的倍立方、三等分角按其表述不可解,描述可作图多边形的特征(高斯层给出这一特征,但没有证明可作图多项式的完整。所有已知完整证明都需要伽罗瓦理论。)
伽罗瓦最初使用置换群来描述给定的多项式的根与係數间的关系。约瑟夫·刘维尔在伽罗瓦去世14年后将他的著作编辑成册并出版。伽罗瓦理论在数学结流行起来需要更长时间。戴德金(Julius Wilhelm Richard Dedekind)、利奥波德·克罗内克(Leopold Kronecker)、埃米爾·阿廷(Emil Artin)等人发展起来的现代伽罗瓦理论引入了关于域扩张及其自同构的研究。
伽罗瓦理论的进一步抽象为伽罗瓦连接与格罗滕迪克伽罗瓦理论。
在经典问题上的应用[编辑]
伽罗瓦理论的诞生最初是由于如下的现在称之为阿贝尔-鲁菲尼定理的问题,19世纪初之前一直是主要的未解决数学问题之一:
| “ | 为什么五次及更高次的一元多项式方程没有一般的代数解法,即这样的方程不能由方程的系数经有限次四则运算和开方运算求根? | ” |
阿贝尔-鲁菲尼定理提供了一个反例,证明对一部分多项式方程不存在这样的公式。伽罗瓦理论为这问题提供了更完整的解答,而且详细的解释了为什么四次及更低次方程有代数解,以及它们的代数解为什么是那样的形式。此外,它还提供了一种确定特定方程可不可解的方法,这种方法概念清晰,易于用算法表示。
伽罗瓦理论还对尺规作图问题提出了清晰的洞察,给出了所有可以尺规作图的长度比的一个优雅描述。这样,一些经典几何问题的解答变得相对容易:
| “ | 哪些正多边形是可以尺规做出的? | ” |
| “ | 为何不能三等分任意角? | ” |
| “ | 尺规作图为何无法实现倍立方? | ” |
历史[编辑]
伽罗瓦之前[编辑]
伽罗瓦理论源于对称函数研究,即首一多项式的系数(在符号意义上)是根的初等对称多项式。例如,,其中1、、是0、1、2次二元初等多项式。
16世纪法国数学家弗朗索瓦·韦达在韦达定理中首次正式表述了正实数根的情形。18世纪英国数学家查尔斯·赫顿认为[2],用多项式系数表示方程的根(不只是正根)的方法始见于17世纪法国数学家Albert Girard,赫顿这样写道:
...[Girard是]第一个理解由根及其乘积之和形成幂的系数的一般学说的人。他是第一个发现任何方程根的幂的求和规则的人。
因此,判别式是根的对称函数,反映了根的性质:当且仅当多项式有重根时,判别式为零;对于2、3次多项式,当且仅当所有根都是互不相等的实数时,判别式为正;当且仅当有一对不同的复共轭根时,判别式为负。
15–16世纪意大利数学家希皮奥内·德尔·费罗首次发现了部分一元三次方程的解法,但没有公布自己的成果。1535年,尼科洛·塔尔塔利亚独立发现了这套解法,并与吉罗拉莫·卡尔达诺分享,但要求他不要发表。卡尔达诺用类似方法将其推广,可见三次方程#卡尔达诺法。发现德尔·费罗的研究后,他认为塔尔塔利亚的方法不再是秘密,因此在《大术》(Ars Magna,1545)中发表了自己的解法。[3]他的学生洛多维科·费拉里解出了一元四次方程,解法也收录在《大术》中。不过书中没有一元三次方程解的一般式,因为那时还没有复数和充足的代数符号来描述一般三次方程。用现代符号与复数可以验证,书中公式在一般情形下确实有效,但卡尔达诺不知道。拉斐尔·邦贝利设法用复数求解所有形式的三次方程。
法国意大利裔数学家约瑟夫·拉格朗日的论文《关于代数方程解的思考》(Réflexions sur la résolution algébrique des équations,1770)在拉格朗日预解式法中,分析了卡尔达诺和费拉里的解法,认为其根的排列组合(置换)可以得到低次的辅助多项式,从而对解法有了统一认识,并为群论与伽罗瓦理论奠定了基础。但至关重要的是,他没有考虑置换的组合。拉格朗日法没有推广到五次及以上的方程,因为预解式的次数更高。
保罗·鲁菲尼在1799年几乎证明了五次方程没有一般的根式解,其中关键是置换群,而非单一的置换。他的证明有缺陷,柯西认为这无伤大雅。挪威数学家尼尔斯·阿贝尔在1824年发表的研究中补全了这缺陷,从而建立了阿贝尔-鲁菲尼定理。
鲁菲尼和阿贝尔确定了一般五次方程不可解,而这种特殊五次方程是可解的。埃瓦里斯特·伽罗瓦找到了五次及以上方程的确切可解指标:多项式是否可解取决于其根的置换群(即其伽罗瓦群)是否具有某种结构(即是不是可解群)。对四次及以下的多项式,这个群总可解;而五次及以上的多项式则不总是可解的。
伽罗瓦[编辑]

1830年,18岁的伽罗瓦向巴黎科学院提交了一份备忘录,介绍了他的根式可解性理论。次年,他的文章因过于简略和给出的是方程根(而非系数)的条件而被否决。随后,伽罗瓦在1832年的一场决斗中丧生,他的论文《根式方程可解条件备忘录》(Mémoire sur les conditions de résolubilité des équations par radicaux)到1846年才由约瑟夫·刘维尔发表,并附有他自己的一些解释。[4]刘维尔在1843年7月4日的一次演讲中向学院宣布了伽罗瓦的结果。[5]Allan Clark认为,伽罗瓦的描述“极大地取代了阿贝尔和鲁菲尼的工作”。[6]
后续[编辑]
众所周知,伽罗瓦理论很难为同时代的人理解。例如,刘维尔在1846年的评论中完全忽略了群论这一方法核心。[7]约瑟夫·阿尔弗雷德·塞雷曾参加过几次刘维尔的演讲,将伽罗瓦理论写入了1866年的教科书《高等代数》(Cours d'algèbre supérieure,第3版)。他的学生卡米尔·若尔当在《关于替代和代数方程》(Traité des substitutions et des équations algébriques,1870)中对伽罗瓦理论有了更深刻的理解。法国之外,伽罗瓦理论在更长的时期中仍然比较模糊。英国数学家阿瑟·凯莱没能领会伽罗瓦理论的深刻内涵,英国流行的代数教科书到20世纪初才提到伽罗瓦理论。德国数学家利奥波德·克罗内克的著作更关注阿贝尔的结果;理查德·戴德金对伽罗瓦理论著述甚少,但在1858年于哥廷根大学发表了关于伽罗瓦理论的演讲,显示了他的深刻理解。[8]1880年代,欧根·内托根据若尔当的《关于替代和代数方程》编写的书,以及海因里希·马丁·韦伯1895年出版的代数教科书,让更多德国和美国读者了解了伽罗瓦理论。[9]
置换群描述[编辑]
给定一多项式,它的一些根可能是被不同的多项式方程联系起来的。例如,有两个根A和B,满足方程。伽罗瓦理论的核心思想是考虑具有以下性质的根的置换:根满足的任何多项式方程,在置换之后仍成立。此理论最初是针对有理系数代数方程提出的,其实可以自然扩张到系数位于任意域的方程,但简单起见,我们限制在有理数域。
这些置换形成了一个置换群,也称为多项式的伽罗瓦群,可以很清晰的举例说明。
例1:二次方程[编辑]
考虑一元二次方程:
应用一元二次方程的求根公式,可得其两个根
A和B满足一些多项式方程:
这些方程中,交换A和B,方程恒成立。例如,方程A + B = 4简单的变成了B + A = 4。进一步的,这对于A和B满足的所有可能的多项式方程都成立。这是对称多项式理论的成果,这里可以用二项式定理的公式来代替。
这里会有人产生疑问:A和B同样满足另一个多项式方程,但交换A和B后,这个方程将不成立。不过,这里不考虑这种关系,因为它的系数是无理数。
我们可以总结出,多项式的伽罗瓦群由两种置换构成:保持A和B不变的恒同变换,以及交换A与B位置的换位。它是一个二阶循环群,因此同构于。
类似讨论适用于任意二次多项式,其中a、b、c都是有理数。
- 如果多项式只有一个有理根,例如,则伽罗瓦群是平凡的,即只包括恒同变换。
- 如果多项式有两个不同的有理根,例如,伽罗瓦群同样是平凡的。
- 如果多项式有两个无理根(包括根是复数的情况),那么伽罗瓦群包括上面例子中所描述的两个置换。
例2:四次方程[编辑]
考虑多项式
也可以写成
我们同样希望在有理数域上描述这多项式的伽罗瓦群。这个多项式有四个根:
这四个根有24种可能的排列,但它们并不都是伽罗瓦群的元素。伽罗瓦群的元素必须保持所有A, B, C和D满足的有理系数多项式方程。这样的方程例如:
由此可知,如果φ是属于伽罗瓦群的置换,则必须有:
因此置换由A的像确定,伽罗瓦群有4个元素:
现代的域论描述[编辑]
现代的研究方法是从域扩张L/K开始,并分析固定K的L的自同构群。进一步的解释和例子请参见关于伽罗瓦群条目。
这两种描述的关系如下。多项式系数属于基域K;扩域L应是在域K中添加多项式的根得到的域。满足保上述多项式方程的根的置换,都对应L/K的一个自同构,反之亦然。
在上面的第一个例子中,我们研究的是域扩张,其中是有理数域,而是在中加入得到的域。在第二个例子中,我们研究的是域扩张。
现代的方法比起置换群方法,有几点优势:
- 它使得伽罗瓦理论基本定理的描述更为简洁;
- 在数学中的很多其他领域需要使用Q以外的基域。例如,在代数数论中,人们经常在代数数域、有限域和局部域上应用伽罗瓦理论。
- 它使人们更容易研究无穷扩张。这在代数数论中同样很重要,例如人们经常需要研究Q的绝对伽罗瓦群,即当K是Q的一个代数闭包时,K/Q的伽罗瓦群。
- 它使得人们可以研究不可分扩张。这在经典框架中并不成为问题,因为这时总是可以假定为特征0的;但在数论和代数几何中经常出现特征非0的情况。
- 它去除了人们对多项式求根的依赖性。也就是说,不同的多项式可能产生同一个扩域,现代的方法可以识别这些多项式之间的联系。
可解群和根式解[编辑]
群論中可解群的概念讓我們得以確定多項式何時有根式解,这取决于其伽罗瓦群是否有可解性。每个域扩张实质上都对应伽罗瓦群合成列中的某因子群。若合成列的某因子群是n阶循环群,且若相应域扩张中,域K已经包含了原始n次单位根,则其就是一个根式扩域,L的元素就可以用K中某元素的n次根表示。若合成列中所有因子群都是循环群,则称此伽罗瓦群可解,相应域中所有元素都可从基域(通常是)通过取根、积、求和得到。
有根式解的充要條件是其分裂域L對基域F的伽羅瓦群可解。簡言之,取此伽羅瓦群的任一合成列,透過伽羅瓦理論基本定理,合成列對應到一族子域,各段的伽羅瓦群一一對應於合成列的因子。若之伽羅瓦群是n階循環群,則域擴張由n次根式生成。伽羅瓦群可解若且唯若合成列的因子皆為循環群,於是若群可解,相應方程便有根式解。反向的結果亦不難證明。 伽羅瓦理論的重大成就之一是證明了當時,一般的n次多項式無根式解(「一般」意謂將多項式係數視為獨立變元)(几年前尼尔斯·阿贝尔用相似方法独立证明了这一点,这就是阿贝尔-鲁菲尼定理),并得到了检验多项式是否根式可解的方法。原因是對稱群在時包含的正规子群中有个单群是交错群,不是循环群,因此不可解。
例3:不可解的五次方程[编辑]
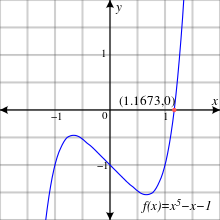
以多项式方程 为例。[10] 根据有理数根定理,方程无有理零点,也无模2或3的线性因子。模2的伽罗瓦群是6阶循环群,因为模2可以分解为2、3次多项式:。
模3无线性或二次因子,因此是不可还原的,于是其模3伽罗瓦群包含5阶元素。
众所周知[11],素数模的伽罗瓦群同构于有理数上伽罗瓦群的一个子群。
5个对象(其中包含5、6阶元素)上的置换群只能是对称群,因此对称群就是的伽罗瓦群,故无根式解。
这是不可解五次多项式最简单的例子之一。塞尔日·兰说埃米尔·阿廷很喜欢这个例子。[12]
逆伽罗瓦问题[编辑]
逆伽罗瓦问题是寻找具有给定伽罗瓦群的域扩张的问题。
不指定基域的话问题并不难,而且所有有限群都能作为伽罗瓦群出现。证明这一点可以这样做:选定域K和有限群G。凯莱定理指出,G(在同构意义上)是对称群S在G的元素上的子群。选择不定项,G的每个元素对应一个不定项,与K相配得到域。F中包含了中的对称有理函数域L。根据埃米尔·阿廷的基本结果,的伽罗瓦群是S。G通过S的作用的限制作用于F,若此作用的定域是M,则据伽罗瓦理论基本定理,的伽罗瓦群就是G。
另一方面,是否每个有限群都能作为有理数域某域扩张的伽罗瓦群,仍是未知的。伊戈尔·沙法列维奇证明可解有限群都是的某扩张的伽罗瓦群。很多人已解决了某些非阿贝尔单群的逆伽罗瓦问题。在26个散在单群中,除马蒂厄群外,其他解都已证明了存在性。甚至还有一种整系数多项式,其伽罗瓦群是魔群.
不可分扩张[编辑]
在上述形式中,特别是伽罗瓦理论基本定理中,只考虑伽罗瓦扩张,是可分扩张。一般的域扩张可以分为可分扩张与纯不可分扩张,对后者如,有一种伽罗瓦理论,其中伽罗瓦群被导子的向量空间取代,即满足莱布尼茨法则的F的K-线性自同态。这种对应关系中,中介域F被赋予。相反,满足进一步适当条件的子空间映射到。在的假设下,Jacobson (1944)证明,这建立了一一对应关系。Brantner & Waldron (2020)利用导出代数几何概念给出对应关系,消除了Jacobson提出的条件。
另见[编辑]
注释[编辑]
- ^ 1.0 1.1 Stewart, Ian. Galois Theory. Chapman and Hall. 1989. ISBN 0-412-34550-1.
- ^ Funkhouser 1930
- ^ Cardano 1545
- ^ Tignol, Jean-Pierre. Galois' Theory of Algebraic Equations
 . World Scientific. 2001: 232–3, 302. ISBN 978-981-02-4541-2.
. World Scientific. 2001: 232–3, 302. ISBN 978-981-02-4541-2.
- ^ Stewart, 3rd ed., p. xxiii
- ^ Clark, Allan. Elements of Abstract Algebra. Courier. 1984: 131 [1971]. ISBN 978-0-486-14035-3.
- ^ Wussing, Hans. The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory. Courier. 2007: 118. ISBN 978-0-486-45868-7.
- ^ Scharlau, Winfried; Dedekind, Ilse; Dedekind, Richard. Richard Dedekind 1831–1981; eine Würdigung zu seinem 150. Geburtstag (PDF). Braunschweig: Vieweg. 1981. ISBN 9783528084981.
- ^ Galois, Évariste; Neumann, Peter M. The Mathematical Writings of Évariste Galois. European Mathematical Society. 2011: 10. ISBN 978-3-03719-104-0.
- ^ van der Waerden, Modern Algebra (1949 English edn.), Vol. 1, Section 61, p.191
- ^ Prasolov, V.V. 5 Galois Theory Theorem 5.4.5(a). Polynomials. Algorithms and Computation in Mathematics 11. Springer. 2004: 181–218. ISBN 978-3-642-03979-9. doi:10.1007/978-3-642-03980-5_5.
- ^ Lang, Serge. Algebraic Number Theory. Graduate Texts in Mathematics 110. Springer. 1994: 121. ISBN 9780387942254.
参考文献[编辑]
- Harold M. Edwards. Galois Theory. Springer-Verlag. 1984. ISBN 978-0-387-90980-6.
- Serge Lang, 'Algebraic Number Theory', Addison-Wesley (1970).
- Artin, Emil. Galois Theory. Dover. 1998 [1944]. ISBN 0-486-62342-4.
- Bewersdorff, Jörg. Galois Theory for Beginners: A Historical Perspective. The Student Mathematical Library 35. American Mathematical Society. 2006. ISBN 0-8218-3817-2. S2CID 118256821. doi:10.1090/stml/035.
- Brantner, Lukas; Waldron, Joe, Purely Inseparable Galois theory I: The Fundamental Theorem, 2020, arXiv:2010.15707

- Cardano, Gerolamo. Artis Magnæ (PDF). 1545 (拉丁语).
- Edwards, Harold M. Galois Theory
 . Springer-Verlag. 1984. ISBN 0-387-90980-X. (Galois' original paper, with extensive background and commentary.)
. Springer-Verlag. 1984. ISBN 0-387-90980-X. (Galois' original paper, with extensive background and commentary.) - Funkhouser, H. Gray. A short account of the history of symmetric functions of roots of equations. American Mathematical Monthly. 1930, 37 (7): 357–365. JSTOR 2299273. doi:10.2307/2299273.
- Hazewinkel, Michiel (编), Galois theory, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
- Jacobson, Nathan, Galois theory of purely inseparable fields of exponent one, Amer. J. Math., 1944, 66 (4): 645–648, JSTOR 2371772, doi:10.2307/2371772
- Jacobson, Nathan. Basic Algebra I 2nd. W. H. Freeman. 1985. ISBN 0-7167-1480-9. (Chapter 4 gives an introduction to the field-theoretic approach to Galois theory.)
- Janelidze, G.; Borceux, Francis. Galois Theories. Cambridge University Press. 2001. ISBN 978-0-521-80309-0. (This book introduces the reader to the Galois theory of Grothendieck, and some generalisations, leading to Galois groupoids.)
- Lang, Serge. Algebraic Number Theory. Berlin, New York: Springer-Verlag. 1994. ISBN 978-0-387-94225-4.
- Postnikov, M. M. Foundations of Galois Theory. Dover Publications. 2004. ISBN 0-486-43518-0.
- Rotman, Joseph. Galois Theory 2nd. Springer. 1998. ISBN 0-387-98541-7.
- Völklein, Helmut. Groups as Galois groups: an introduction
 . Cambridge University Press. 1996. ISBN 978-0-521-56280-5.
. Cambridge University Press. 1996. ISBN 978-0-521-56280-5. - van der Waerden, Bartel Leendert. Moderne Algebra. Berlin: Springer. 1931 (德语).. English translation (of 2nd revised edition): Modern Algebra
 . New York: Frederick Ungar. 1949. (Later republished in English by Springer under the title "Algebra".)
. New York: Frederick Ungar. 1949. (Later republished in English by Springer under the title "Algebra".)
外部链接[编辑]
以下是一些網上的教學資料:
- ABSTRACT ALGEBRA ON LINE: Galois Theory(页面存档备份,存于互联网档案馆) (英文)
- nrich.maths.org Mathematics Enrichment: An Introduction to Galois Theory(页面存档备份,存于互联网档案馆) (英文)
中英夾雜的教學資料:
以下網站提供德语、中文、英语、法语、意大利语、西班牙语及罗马尼亚语版的線上教材:
- Evariste Galois: whatsnew(页面存档备份,存于互联网档案馆) (英文)
以下網站提供伽羅瓦生平及其理論的應用:
|

























































