擬柱體
外觀
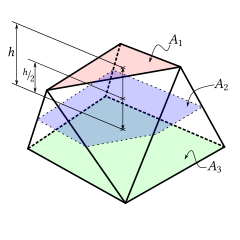
擬柱體(prismatoid)是指所有的頂點都在兩個平行平面中的多面體。其側面可能是三角形、梯形或平行四邊形。[1]如果兩個平行面的頂點數相同,且側面為平行四邊形或梯形,則稱為稜錐台[2](prismoid)[3],而此處的稜錐台與錐台並不等價[4]。
一般的柱體、稜台、帳塔、球枱等都屬於擬柱體。由於擬柱體必須滿足頂點都在兩個平行平面的條件,因此部分的柱狀立體、盾片狀和罩帳皆不屬於擬柱體。
性質
[編輯]其中,h為高,在高度平行於底面的截面積;,高度h,就是頂面;,高度0,就是底面。
其來源為對不超過三次的多項式,以辛普森積分法求定積分之結果。
例子
[編輯]| 錐體 | 楔體 | 平行六面體 | 稜柱 | 反稜柱 | 帳塔 | 錐台 | ||
|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

| |||
參考文獻
[編輯]- ^ William F. Kern, James R Bland, Solid Mensuration with proofs, 1938, p.75
- ^ 稜錐台 prismoid. 樂詞網, 國家教育研究院. [2023-01-09]. (原始內容存檔於2023-01-09).
- ^ Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey: Solid Geometry in the 21st Century. The Mathematical Association of America, 2015, ISBN 9780883853580, pp. 85-89
- ^ 錐台 frustum. 樂詞網, 國家教育研究院. [2023-01-09]. (原始內容存檔於2023-01-09).
- ^ B. E. Meserve, R. E. Pingry: Some Notes on the Prismoidal Formula. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263
| 這是一篇關於幾何學的小作品。您可以透過編輯或修訂擴充其內容。 |





