混沌理論

數值r = 28，σ = 10，b = 8/3的勞侖次吸引子圖形。

一個雙杆擺動畫呈現混沌行為。 從開始略微不同的初始條件擺杆將導致一個完全不同的軌跡。雙杆擺是具有混沌方案最簡單的動態系統之一。

杜芬方程式吸引子圖列

蔡氏電路 吸引子

Rossler 吸引子

陳氏吸引子

混沌理論（英語：Chaos theory）是關於非線性系統在一定參數條件下展現分岔、週期運動與非週期運動相互糾纏，以至於通向某種非週期有序運動的理論。在耗散系統和保守系統中，混沌運動有不同表現，前者有吸引子，後者無（也稱含混沌吸引子）。

從20世紀80年代中期到20世紀末，混沌理論迅速吸引了數學、物理、工程、生態學、經濟學、氣象學、情報學等諸多領域學者有關注，引發了全球混沌熱。混沌，也寫作渾沌（比如《莊子》）。自然科學中講的混沌運動指確定性系統中展示的一種類似隨機的行為或性態。確定性是指方程式不含隨機項的系統，也稱動態系統。典型的模型有單峰映象迭代系統，洛倫茲微分方程式系統，若斯叻吸引子，杜芬方程式，蔡氏電路，陳氏吸引子等。為渾沌理論做出重要貢獻的學者有龐加萊、洛倫茲、上田睆亮、費根堡姆、約克、李天岩、斯美爾、芒德勃羅等。混沌理論向前可追溯到19世紀龐加萊等人對天體力學的研究，他提出了同宿軌道、異宿軌道的概念，他也被稱為渾沌學之父。

混沌行為可以在許多自然系統中被觀測到，例如天氣和氣候。對於這個行為的研究，可以通過分析混沌數學模型，或者通過諸如遞迴圖和龐加萊對映等分析技術。

定義

混沌理論是一種兼具質性思考與量化分析的方法，用以探討動態系統中無法用單一的資料關係，而必須用整體，連續的資料關係才能加以解釋及預測之行為。

“ 一切事物的原始狀態，都是一堆看似毫不關聯的碎片，但是這種混沌狀態結束後，這些無機的碎片會有機地匯整合一個整體。 ”

混沌一詞原指發現宇宙混亂狀態的描述，古希臘哲學家對於宇宙之源起即持混沌論，主張宇宙是由混沌之初逐漸形成現今有條不紊的世界。在井然有序的宇宙中，科學家經過長期的探討，逐一發現眾多自然界中的規律，如大家熟知的萬有引力、槓桿原理、相對論等。這些自然規律都能用單一的數學公式加以描述，並可以依據此公式準確預測物體的行徑。

近半世紀以來，科學家發現許多自然現象即使可以化為單純的數學公式，但是其行徑卻無法加以預測。如氣象學家愛德華·諾頓·勞侖次發現簡單的熱對流現象居然能引起令人無法想像的氣象變化，產生所謂的「蝴蝶效應」。60年代，美國數學家史蒂芬·斯梅爾發現某些物體的行徑經過某種規則性變化之後，隨後的發展並無一定的軌跡可循，呈現失序的混沌狀態。

背景

利用混沌遊戲製作的巴恩斯利蕨。自然形態（蕨類、雲、山脈等等）可通過迭代函式系統（IFS）再現。

詹姆斯·克拉克·麥克斯韋首先強調了「蝴蝶效應」，並被認為是最早討論混沌理論的人之一，在1860年代到1870年代有相關研究。1880年代亨利·龐加萊在研究三體問題時發現，存在非週期性軌道，但既不會永遠增加，也不會趨近於定點。1898年，雅克·阿達馬發表了一篇影響深遠的研究報告，研究了在恆定負曲率表面上無摩擦滑動的自由粒子的混沌運動，形成「阿達馬動態系統」。阿達馬證明所有軌跡都不穩定，都會以指數形式相互發散，且具有正的李雅普諾夫指數。

混沌理論始於遍歷理論。後來，喬治·戴維·伯克霍夫、安德雷·科摩哥洛夫、Mary Lucy Cartwright & 約翰·伊登斯爾·利特爾伍德及史蒂芬·斯梅爾等人也對非線性微分方程式進行了研究。除斯梅爾外，他們都直接受物理學啟發：伯克霍夫的三體問題、科爾莫戈羅夫的湍流和天文問題以及Cartwright和利特爾伍德的無線電工程問題。雖然混沌行星運動尚未被觀測到，但實驗人員已經遇到了流體運動中的湍流和無線電電路中的非週期性振盪，卻沒有理論來解釋這些現象。

混沌系統在20世紀上半葉就已經有了初步的認識，但混沌理論要到世紀中葉之後才正式成立。當時人們發現，流行的線性系統理論無法解釋某些實驗（如邏輯斯蒂對映）的行為。混沌理論認為，測量不精確和簡單的「噪聲」都是研究系統的組成部分。1959年，伯里斯·奇里科夫提出了哈密頓系統出現經典混沌的標準，即奇里科夫標準。他將其解釋了開放鏡俘獲（open mirror trap）中電漿體束縛的一些試驗結果，一般認為這是第一個成功解釋具體實驗現象的混沌物理理論，奇里科夫本人也被視為經典與量子混沌的先驅。

電腦極大推進了混沌理論的發展。混沌理論的大部分數學知識涉及簡單公式的反覆迭代，手工操作是不切實際的。電腦使重複計算變得切實可行，而數字和圖像則使視覺化成為可能。1961年11月27日，京都大學林千博實驗室的研究生上田睆亮在進行類比電腦實驗時，注意到了他所謂「隨機過渡現象」，然而他的導師並不認同他的結論，到1970年才允許他報告自己的發現。

飛機機翼翼尖渦流中的湍流。對系統湍流產生的臨界點研究對混沌理論非常重要。例如，蘇聯物理學家列夫·朗道對臨界點進行了分析，提出了湍流的朗道-霍普夫理論。達維德·呂埃勒和loris Takens則預言，流體湍流可能通過奇異吸引子產生。

愛德華·諾頓·洛倫茨是混沌理論的早期先驅，他對混沌的興趣產生於1961年偶然從事的天氣預報工作。當時，洛倫茲與同事Ellen Fetter、瑪格麗特·漢密爾頓用一台簡單的數字電腦——Royal McBee LGP-30執行天氣類比。他們想再看一次資料，為了節省時間，在類比過程的中間開始了類比。他們輸入了與原類比中間條件對應的資料，並進行類比。然而，這次預測與之前的結果完全不同。電腦以6位精度執行，列印輸出將變數捨入到3位，當時的共識是這種微小差異不會產生實際影響；洛倫茲發現，初始條件的微小變化會導致長期結果的巨大變化。洛倫茲的發現表明，即使是詳細的大氣模型，一般來說也做不出精確的長期天氣預測。

1963年，本華·曼德博在研究資訊理論時發現，許多現象（如股價與電話線路）中的噪聲模式類似於康托爾集，是具有無限糙度和細節的點集。曼德博總結出「諾亞效應」（可能發生突然的不連續變化）和「約瑟夫效應」（一個值可能持續一段時間，之後又發生突變）。他發表的《英國的海岸線有多長？統計自相似和分數維度》（1967）指出海岸線的長度隨測量儀器的尺度而變化，在所有尺度上都與自身相似，對於無窮小的儀器來說，海岸線的長度是無限的。從遠處看麻繩球是一個點（0維），從近處看是一個球（3維），再近了看是一條彎曲的繩（捲曲的1維），他認為從這個例子看，物體的維度是相對於觀察者而言的，且可能是分數。物體在不同尺度上的不規則性（「自相似性」）是一定的，這個物體就是碎形（如門格海綿、謝爾賓斯基三角形和科赫雪花，雪花無限長卻包圍著有限的空間，其碎形維度約為 1.2619）。1982年，曼德博出版了《大自然的碎形幾何學》，成為混沌理論的經典之作。

1977年12月，紐約科學院組織了第一次混沌研討會，達維德·呂埃勒、Robert May、詹姆士·約克（數學中「混沌」的引入者）、Robert Shaw及氣象學家愛德華·洛倫茲出席了會議。次年Pierre Coullet和Charles Tresser發表了《自同態迭代與重整化群》（Itérations d'endomorphismes et groupe de renormalisation），米切爾·費根鮑姆《一類非線性轉換的定量普遍性》（Quantitative Universality for a Class of Nonlinear Transformations）在被審稿人拒稿了3年後終於發表了出來。因此，費根鮑姆 (1975)和Coullet & Tresser (1978)發現了混沌的普遍性，從而混沌理論將可用於許多不同的現象。

1979年，Albert J. Libchaber在皮埃爾·奧昂貝格於阿斯彭組織的一次研討會上，介紹了對導致瑞利-貝納德對流系統混沌與湍流的分岔級聯的實驗觀察。1986年，他與米切爾·費根鮑姆共同被授予沃爾夫物理學獎，以表彰他們取得的鼓舞人心的成就。 1986年，紐約科學院、美國國家心理健康研究所與美國海軍研究辦公室共同組織了第一次關於生物學與醫學中的混沌的會議，會上Bernardo Huberman提出了精神分裂症患者眼動追蹤功能障礙的數學模型。這引發了20世紀80年代生理學在病理心動週期研究等混沌理論應用方面的創新。 1987年，Per Bak、湯超和Kurt Wiesenfeld在《物理評論快報》上發表論文，首次描述了自組織臨界性（SOC），認為這是自然界中複雜性產生的機制之一。

除了阿貝爾沙堆模型等以實驗為基礎的研究方法外，有很多研究聚焦於顯示標度不變性的大規模自然與社會系統上。儘管這些方法並不總是得到領域專家的歡迎（至少最初如此），SOC還是成為了解釋諸多自然現象的有力候選，如地震（SOC之前，就已經知道地震是一種標度不變行為，如描述地震規模統計分布的古登堡-里克特定律，以及描述餘震頻率的大森定律）、耀斑、金融市場等經濟系統的波動（經濟物理學中常見SOC）、地貌形成、森林火災、山崩、流行病與演化（SOC被援引為尼爾斯·艾崔奇與史蒂芬·古爾德提出的「間斷平衡」依據的動力機制）。參考時間規模的無標度分布的含義，有人認為戰爭也是SOC的例子。這些對SOC的研究有嘗試建模（開發新模型，或據自然系統的具體情形調整現有模型）、廣泛資料分析等，以確定自然縮放規律的存在和/或特徵。

同年，詹姆斯·格雷克出版了《混沌：創造一門新科學》（Chaos: Making a New Science），迅速成為暢銷書，向一般大眾介紹了混沌理論的一般原理及其歷史。混沌理論最初只是少數人的研究領域，後來逐漸擴張成跨學科的學科，主要以非線性系統分析的名義出現。許多「混沌學家」引托馬斯·庫恩《科學革命的結構》（1962）提出的「典範轉移」概念，稱這一理論就是典範轉移的例子。格雷克也持這種觀點。

更便宜、更強大的電腦擴大了混沌理論的適用範圍。混沌理論目前仍是很活躍的研究領域，涉及許多不同的學科，如數學、拓撲學、物理學、社會系統、人口模型、生物學、氣象學、天體物理學、資訊理論、計算神經科學、流行病危機管理等等領域。

洛倫茲對混沌建模的開創性貢獻

1963年美國氣象學家愛德華·勞侖次提出混沌理論（Chaos），非線性系統具有的多樣性和多尺度性。混沌理論解釋了決定系統可能產生隨機結果。理論的最大的貢獻是用簡單的模型獲得明確的非週期結果。在氣象、航空及航天等領域的研究裡有重大的作用。 洛倫茲教授在整個職業生涯中，共撰寫了61篇研究論文，其中58篇為其獨作。從1960年在日本召開的會議開始，洛倫茲踏上了開發各種模型的歷程，試圖揭示SDIC和混沌特徵。最近對洛倫茲從1960年到2008年的模型進展的回顧顯示，他善於利用各種物理系統來說明混沌現象，如准地轉系統、恆渦度方程式、瑞利-貝納德對流方程式和淺水方程式等，此外還較早應用了邏輯斯蒂對映探索混沌解，這是他領先於同行取得的里程碑式成就（如Lorenz 1964）。

混沌動力學

x → 4 x (1 – x)與y → (x + y) mod 1定義的對映，展示了對初始x值的敏感性。其中，兩個x、y序列隨時間推移，從微小的初值差異發散出去。

通常來說，「混沌」意味著「無序狀態」。混沌也不存在公認的數學定義，Robert L. Devaney總結出比較常用的定義，指出混沌系統有三種性質：

1. 受初始狀態影響的敏感性，初始條件非常微小的變動也可以導致最終狀態的巨大差別。
2. 具有拓撲混合性；不嚴格地來說，就是系統會將初始空間的拓撲性質徹底打亂，使得任何初始狀態轉換到其他任何位置。
3. 週期軌道稠密，即在任何初始值附近都可以找到具有週期軌道的值。

在離散時間情形下，對初始條件的敏感性對度量空間上所有的連續對映都正確。敏感性是最具實際意義的特性，不過一般無需在定義中加以說明。

若將注意力放在區間上，那麼第二條特性可以推導出另兩條特性。混沌的另一個定義一般較弱，只使用前兩條屬性。

對初始條件的敏感性

主條目：蝴蝶效應

用於生成y變數曲線圖的洛倫茲方程式。x與z的初始條件保持不變，但y的初始條件在1.001、1.0001、1.00001之間變化。$\rho$、$\sigma$、$\beta$的值分別為45.92、16、4 。從圖中可以看出，即使是最細微的差別，也會在大約12秒後發生顯著變化，這就是對初始條件敏感的一個例子。

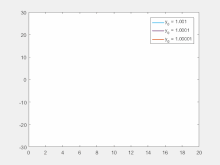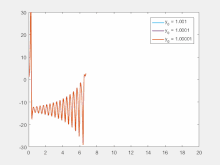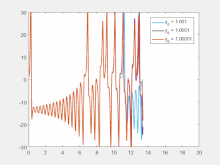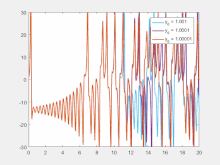
對初始條件的敏感性意味著，混沌系統中的每對極相近的點，會有大相逕庭的軌跡；當前軌跡的任意微小變化都會導致未來行為的顯著不同。

這種性質通常稱作「蝴蝶效應」，源於愛德華·洛倫茲在美國科學促進會上發表的《可預測性：巴西的蝴蝶扇動翅膀會引發德克薩斯州的龍捲風嗎？》（1972）。蝴蝶扇動翅膀代表系統初始條件的微小變化，引發了一連串現象，其出現完全無法預測。倘若蝴蝶沒有扇動翅膀，整個系統的軌跡都會大不相同。

正如洛倫茲在《混沌的本質》（1993）中所寫：「敏感依賴性可以作為混沌的一個可接受定義。」為說明時變路徑對初始位置的敏感性，我們建立了一個理想化的滑雪模型。可預測性水平線可以在SDIC開始之前確定（即在附近初始軌跡出現顯著分離之前）。

若從有限的系統資訊開始（實際情況一般如此），則在一定時間後，系統就不再可預測了。這常見於天氣預報，一般只能提前一周左右。這不是說不能對遙遠未來的事件做出任何斷言，只是說系統存在限制。例如，地表溫度不會自然達到100 °C（212 °F）或低於−130 °C（−202 °F）（當前地質年代），但並沒有方法推知一年中最熱的一天會是哪一天。

李亞普諾夫指數衡量了對初始條件的敏感度，其形式是與擾動的指數發散率。給定相空間中兩個無限接近的初值，初始分離度$\delta \mathbf {Z} _{0}$，兩條軌跡最終發散的速度由以下公式給出：

$|\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,$

其中$t$是時間，$\lambda$是李亞普諾夫指數。分離率取決於初始分離向量的方向，因此可能存在完整的李亞普諾夫指數譜。李亞普諾夫指數的個數等於相空間維數，通常僅指最大的一個：最大李亞普諾夫指數（MLE）最常用，反映系統整體的可預測性。系統MLE若為正，則視作處於混沌狀態。

除上述特性外，還有其他相關性質，例如測度論混合性（如遍歷理論）及K系統的特性。

非週期性

混沌系統可能具有完全重複的演化變數值序列，從序列任一點出發都會產生週期性行為。但這種週期序列是排斥性的：若演化變數在序列之外，無論多麼接近，都不會進入序列，事實上還會偏離。因此，在幾乎所有初始條件下，變數都會以非週期性方式混沌演化。

拓撲混合

一組狀態$[x,y]$通過邏輯斯蒂對映的6次迭代。第一次（藍）為初始條件，基本上形成了一個圓。動畫顯示了圓形為初態的1~6次迭代，可以發現會出現混合現象。第6次迭代中，點幾乎完全分散在相空間中。若進一步迭代，混合將是均勻、不可逆的邏輯斯蒂對映方程式為$x_{k+1}=4x_{k}(1-x_{k})$。將其狀態空間推廣到2維，要建立第二個狀態$y$：$y_{k+1}=x_{k}+y_{k}$，即$x_{k}+y_{k}<1$，否則$y_{k+1}=x_{k}+y_{k}-1$。

x → 4 x (1 – x)與y → (x + y) mod 1定義的對映，也展現出拓撲混合。藍色在動力作用下首先變為紫色，然後到粉色與紅色，最終變為一團散布在空間中的垂直線。

拓撲混合（或較弱的拓撲遞移）是指系統相空間的任意給定區域或開集，隨時間推移都將與任意給定區域重疊。這種「混合」的概念與標準直覺相對，染料或液體的混合就是一種混沌系統。

混沌的流行說法往往忽略了拓撲混合，認為混沌只等同於對初態的敏感性；但這並不會導致混沌。例如，考慮只會將初值反覆加倍的動態系統。它對各處的初值都敏感，因為任意一對鄰近的點都會變得相距甚遠；但由於沒有混合，所以沒有混沌。其實它的行為極其簡單：除了0之外，所有點都趨於無窮大。

拓撲遞移

若對任意一對非空開集$U,V\subset X$，都$\exists k>0$使$f^{k}(U)\cap V\neq \emptyset$，則稱對映$f:X\to X$具有拓撲遞移性。這弱於拓撲混合。直觀地說，給定點x與V，則在x附近存在點y，其在拓撲遞移對映中的軌道穿過V。這說明，不可能將系統分解為兩個開集。

不難看出，稠密軌道意味著拓撲遞移性。伯克霍夫遞移性定理指出，若X是第二可數完備空間，則拓撲遞移性意味著X中存在具有稠密軌道的稠密點集。

稠密週期軌道

具有稠密週期軌道的混沌系統意味著空間中的點都任意接近週期軌道。由x → 4 x (1 – x)定義的1維邏輯斯蒂對映是具有稠密週期軌道的最簡單系統之一。例如，${\tfrac {5-{\sqrt {5}}}{8}}$ → ${\tfrac {5+{\sqrt {5}}}{8}}$ → ${\tfrac {5-{\sqrt {5}}}{8}}$（或約0.3454915 → 0.9045085 → 0.3454915）是週期為2的（不穩定）軌道，而週期為4、8、16等（實際上是沙爾科夫斯基定理指定的所有週期）也存在類似軌道。

沙爾科夫斯基定理是Li & Yorke (1975)的基礎，其證明了任何連續1維系統若表現出週期為3的規則週期，也會表現出其他長度的規則週期以及完全混亂的軌道。

奇異吸引子

洛倫茲吸引子顯示出混沌行為。這兩幅圖顯示了吸引子所占據的相空間區域內初始條件的敏感性。

x → 4 x (1 – x)定義的1維邏輯斯蒂對映之類的動態系統在任何地方都是混沌的，但很多時候混沌僅見於相空間的子集。混沌發生在吸引子上時，大量初始條件都將使軌道向混沌區域收斂。

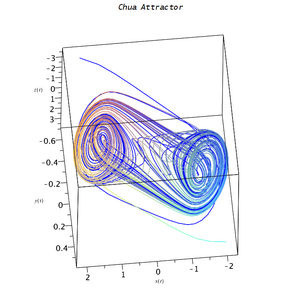
直觀顯示混沌吸引子的簡單方法，是從吸引盆地的某點開始，繪製之後的軌道。由於拓撲遞移，很可能產生整個最終吸引子的圖像。右圖由簡單的洛倫茲天氣系統3維模型產生，都顯示了洛倫茲吸引子的大致形狀，可能是最著名的混沌系統圖示之一，因為它不僅早，也是最複雜的混沌系統圖之一，產生了非常有趣的模式。只要稍加想像，就能看到像蝴蝶翅膀一樣的圖案。

不同於定點吸引子與極限環，混沌系統產生的奇異吸引子具有很強的細節性與複雜性。它出現在連續動態系統（如洛倫茲系統）和一些離散系統（如厄農對映）。其他離散動態系統有一種稱為朱利亞集的排斥結構，形成於定點吸引盆地之間的邊界，可視為奇異吸引子。奇異吸引子具有碎形結構，可以計算碎形維度。

共存吸引子

廣義洛倫茲模型中的共存吸引子與非混沌吸引子。從0.625至5之間的無量綱時間和加熱參數r = 680的不同初始條件開始，共有128條不同顏色的軌道。混沌軌道附近會反覆回到原點的鞍點附近。非混沌軌道最終接近兩個穩定點之一，如藍色大點所示。混沌與非混沌軌道在相空間中占據不同的吸引區。

最近對洛倫茲模型的研究強調了多類解的重要性：相同的建模組態與不同的初始條件下，同一模型（如雙擺系統）可能會出現混沌與非混沌共存的現象。經典與廣義洛倫茲模型得到的吸引子共存結論反映「整個天氣系統具有混沌和有序的雙重性質，具有明顯的可預測性」，這與傳統的「混沌天氣」觀點截然不同。

混沌系統的最小複雜度

邏輯斯蒂對映x → r x (1 – x)的分岔圖。垂直切片對應r值的吸引子。隨著r增加，週期加倍，最終產生混沌。越暗的點被訪問的頻率越高。

邏輯斯蒂對映之類的離散混沌系統，無論維度如何，都會表現出奇異吸引子。具有拋物線最大值和費根鮑姆常數$\delta =4.669201...$,$\alpha =2.502907...$的1維對映的普遍性在作為離散雷射動力模型提出的Tahn對映上清晰可見： $x\rightarrow Gx(1-\mathrm {tanh} (x))$, 其中$x$表示電場振幅，$G$為雷射增益分岔參數，在區間$[0,\infty )$內的逐漸增大會使動力從規則變為混沌，分岔圖與邏輯斯蒂對映的分岔圖具有相同性質。

而連續動態系統，龐加萊-本迪克松定理表明只有在3維及更高維才會出現奇異吸引子。有限維線性系統永遠不會出現混沌，非線性或無限維系統才可能出現混沌。

龐加萊-本迪克松定理指出，二維微分方程式具有非常規則的行為。下面討論的洛倫茲吸引子由以下3個微分方程式的系統產生：

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}$

其中$x$、$y$、$z$構成系統狀態，$t$是時間，$\sigma$、$\rho$、$\beta$是系統參數。右側5個項是線性的，2個是二次項，共有7項。另一個著名的混沌吸引子由若斯叻方程式產生，7個項中只有1個非線性項。Sprott發現了一個只有5項的3維系統，只有1個非線性項，在某些參數值下表現出混沌。Zhang & Heidel證明，對耗散與保守型的二次系統來說，右邊只有3、4項的3維二次系統不會表現出混沌行為。原因很簡單：此類系統的解是二維曲面的漸近，因此解表現良好。

龐加萊-本迪克松定理指出，歐氏平面上的連續動態系統不會是混沌的，非歐幾何的2維連續動態系統則有可能。不過，只要是無限維線性系統，也可能出現混沌。數學分析的一個分支——泛函分析正在發展線性混沌理論。

上面優雅的三個常微分方程式被稱為3維洛倫茲模型。1963年以來，許多研究開發了更高維的洛倫茲模型，用於研究非線性程度的增加及其與加熱、耗散的共同作用對去穩定的影響。

無限維對映

耦合離散對映的直接推廣基於摺積積分，其介導了空間分布對映之間的相互作用： $\psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f[\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}$,

其中的核$K({\vec {r}}-{\vec {r}}^{,},t)$是作為相關物理系統的格林函式匯出的傳播器， $f[\psi _{n}({\vec {r}},t)]$可能是類似$\psi \rightarrow G\psi [1-\tanh(\psi )]$的邏輯斯蒂對映或復對映。復對映的例子是朱利亞集$f[\psi ]=\psi ^{2}$或池田對映$\psi _{n+1}=A+B\psi _{n}e^{i(|\psi _{n}|^{2}+C)}$。考慮波長為$\lambda =2\pi /k$、距離為$L=ct$的波傳播問題時，核$K$可能具有薛丁格方程式的格林函式形式：

$K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{\frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]$.

急動系統

急動度是位置向量相對於時間的三階導，因此微分方程式的形式為

$J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0$

有時也被稱為急動方程式。研究表明，急動方程式等價於3個1階普通非線性微分方程組，從某種意義上說是能產生混沌解的最小設定，激發了學界對急動系統的興趣。涉及4階及以上導數的系統相應地被稱為超急動系統。

急動系統的行為由急動方程式決定，對部分急動方程式，簡單的電子電路就能類比解，稱作急動電路，其可能出現混沌行為。

洛倫茲吸引子和若斯叻吸引子等著名混沌系統，傳統上即描述為由3個1階微分方程組成的系統，可以組合成單一的（相當複雜）急動方程式。急動方程式的另一個例子是：

${\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.$

其中A是可調參數。此方程式在A=3/5時有一個混沌解，可用下面的急動電路實現；所需的非線性由2個二極體產生：

電路中，除$R_{A}=R/A=5R/3$外，所有電阻、電容的大小都相等。主頻為$1/2\pi RC$；運算放大器 0的輸出對應x變數，1的輸出對應x的一階導，2的輸出對應二階導。

類似電路只需要一個二極體或根本不需要二極體。

也可見蔡氏電路，是混沌真亂數發生器的基礎之一。

自發秩序

在適當條件下，混沌會自發演化為一種步調一致的模式。在藏本模型中，有4個條件足以使混沌系統產生同步。例子如惠更斯擺的耦合震盪、螢火蟲、神經元、千禧橋共振、產生約瑟夫森效應的大型陣列等等。

應用

織錦芋螺外殼，與具有混沌行為的細胞自動機「規則30」外觀相似。

混沌理論在許多科學學科中得到廣泛應用，包括：數學、生物學、資訊科技、經濟學、化學、生態學、工程學、金融學、哲學、物理學、政治學、人口學、心理學和機器人學。多種系統的渾沌狀態在實驗室中得到觀察，包括電路、雷射、流體的動態，以及機械和電磁裝置。在自然中進行的有對天氣、衛星運動、天體磁場、生態學中的種群增長、神經元中的動作電位和分子振動的觀察。

密碼學

混沌理論在密碼學中的應用已有多年。過去幾十年中，混沌與非線性動力學已用於涉及數百種加密基元，涉及演算法有圖像加密、雜湊函式、CSPRNG、串流加密法、數位浮水印及隱寫術。它們大多基於單模混沌對映，很大一部分用混沌對映的控制參數與初始條件為金鑰。更廣地看，在不失一般性的前提下，混沌對映與密碼系統的相似，是設計混沌密碼演算法的主要動機。對稱金鑰加密即依賴於混沌理論類比的混淆與擴散。DNA運算與混沌理論相結合，提供了一種加密圖像等資訊的方法。許多DNA-混沌加密演算法都被證明不安全，或者效率不高。

機器人學

機器人學是最近受益於混沌理論的另一個領域。混沌理論主要用於預測建模，而非讓機器人通過試錯與環境互動。被動行走的兩足機器人也表現出了混沌動力。

生物學

這一百多年，生物學家都在試圖用人口模型追蹤不同物種的種群變化。大多數模型都是連續的，但最近在特定種群中，已經有混沌模型的實現。例如，對加拿大猞猁模型的研究表明，種群增長存在混沌行為。渾沌理論最成功的應用之一即在於生態學中的洛特卡－沃爾泰拉方程式，在其中顯示了受密度制約之下的種群增長如何引致混沌狀態。

水文學之類的生態系統中也存在混沌現象，雖然其模型有不足之處，但通過混沌理論的視角觀察資料，仍有很多值得學習的東西。另一個生物學應用是胎心分娩力描記法。胎兒監護需要一種微妙的平衡，要儘可能無創地獲得精確資訊。混沌建模可獲得宮內缺氧的更好模型。

正如Perry指出的，理論生態學中混沌時間序列的建模得益於約束條件。真實的混沌與模型特有的混沌的區分往往有潛在困難，因此直接的約束條件和/或用於比較的重複時序資料都有助於約束模型，使其更接近現實，例如Perry & Wall 1984。基因對基因的共同演化有時會顯示出混沌的基因頻率動態。增加變數會加劇這種情況：在含額外變數的演化模型中，混沌會更常見，以反映真實種群的更多方面。Robert M. May本人也做過一些農作物共同進化的基礎研究，反過來又塑造了整個領域。即使是在穩定的環境中，僅僅將一種農作物與一種病原體結合起來，也可能導致病原體母體的準週期或混沌震盪。

經濟學

混沌理論也有可能改進經濟模型，但預測經濟系統的健康狀況，及分析影響最大的因素是極其複雜的任務。經濟金融體系與經典自然科學體系有著本質區別：前者本質上是人際相互作用的隨機結果，純確定性模型不可能準確反映資料。檢定經濟與金融學中的混沌的實證文獻得出的結果相當不一致，部分原因是混淆了對混沌的特定核對和對非線性關係的更一般檢定。

經濟學中可以通過遞迴量化分析發現混沌現象。事實上，Orlando et al.通過所謂遞推量化相關指數，發現了時序中的隱藏變化。然後，採用相同技術檢測層流（規則）到湍流（混沌）階段的過渡及總體經濟變數之間的差異，並突出經濟動態的隱藏特徵。最後，混沌理論有助於建立經濟執行模型，以及嵌入COVID-19等外部事件造成的衝擊。

管理作業研究

管理作業研究領域的許多混沌系統，如排隊系統、庫存系統、計劃調度系統等的主要特點是在不同的管理決策規則下，隊列、庫存和計劃調度的混亂。 Murphy以混沌理論為模型，研究公共關係管理中的問題和危機。 Joseph在總結混沌管理的研究現狀後指出，混沌管理依賴於變化規則，變化規則是基於有序或無序變化、適應性、新的有序出現過程的一套規則。

混沌控制

混沌控制由狄透（William Ditto）、賈芬卡（Alan Garfinkel）、約克（Jim Yorke），將此想法化為實用技術，用微小的變化開始，造成希望所想的巨大改變。

其他領域

化學中，預測氣體溶解度對生產聚合物至關重要，但使用粒子群最佳化（PSO）的模型往往會收斂到錯誤的點上。一種改進的PSO引入了混沌理論，避免了模型陷入困境。天體力學中，尤其是觀測小行星時，混沌理論可以更好預測它們何時會接近行星。冥王星的5顆衛星中有4顆以混沌方式旋轉。量子力學和電氣工程中，對約瑟夫森效應大型陣列的研究極大受益於混沌理論。煤礦常發生瓦斯洩漏，導致大量傷亡。直到最近，還沒有可靠方法來預測，但它們具有混沌趨勢。如果模型建立得當，可以相當準確地預測。

混沌理論可用於自然科學以外的領域，但歷史上幾乎所有此類研究都缺乏可重複性、外部有效性差、和/或不注重交叉驗證，導致預測準確性差。Glass、Mandell & Selz發現，迄今還沒有任何EEG研究表明存在奇異吸引子或其他混沌行為的跡象。

混沌理論在心理學亦有應用。例如，在類比群體行為時，特殊成員可能分享威爾弗雷德·魯普萊希特·比昂理論中的基本假設。研究人員發現，群體動態是個體動態的結果：每個個體以不同尺度再現群體動態，群體的混沌反映在每個成員身上。

參見

• 混沌系統的實例
  • 蔡氏電路
  • 單峰映象
  • 若斯叻吸引子

• 其他相關主題
  • 條件數
  • 適定性問題
  • 碎形
    • 朱利亞集
    • 曼德博集合
  • 湧現
  • 非線性
  • 聖菲研究所
  • 複雜

• 人物
  • 麥可·貝里
  • 蔡少棠
  • 愛德華·諾頓·勞侖次
  • 亞歷山大·李亞普諾夫
  • 本華·曼德博
  • 儒勒·昂利·龐加萊
  • 詹姆士·約克
• 隨機性
• 分岔
• 決定論
• 非決定論
• 因果律
• 自由意志
• 複雜性
• 系統論
• 蝴蝶效應
• 量子力學

參考文獻

來源

刊物文章

• 郝柏林：《分岔、混沌、奇怪吸引子、湍流及其它》，《物理學進展》，1983， 3（01）.
• 朱照宣：《非線性動力學中的渾沌》，《力學進展》，1984， （02）.

書籍

• 苗東升、劉華傑：《渾沌學縱橫論》，北京：中國人民大學出版社，1992，1993.
• 劉華傑：《渾沌語意與哲學》，長沙：湖南教育出版社，1998.

外部連結

• Hazewinkel, Michiel (編), Chaos, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
• Nonlinear Dynamics Research Group with Animations in Flash
• The Chaos group at the University of Maryland （頁面存檔備份，存於網際網路檔案館）
• The Chaos Hypertextbook （頁面存檔備份，存於網際網路檔案館）. An introductory primer on chaos and fractals
• ChaosBook.org （頁面存檔備份，存於網際網路檔案館） An advanced graduate textbook on chaos (no fractals)
• Society for Chaos Theory in Psychology & Life Sciences （頁面存檔備份，存於網際網路檔案館）
• Nonlinear Dynamics Research Group at CSDC, Florence Italy
• Interactive live chaotic pendulum experiment, allows users to interact and sample data from a real working damped driven chaotic pendulum
• Nonlinear dynamics: how science comprehends chaos （頁面存檔備份，存於網際網路檔案館）, talk presented by Sunny Auyang, 1998.
• Nonlinear Dynamics （頁面存檔備份，存於網際網路檔案館）. Models of bifurcation and chaos by Elmer G. Wiens
• Gleick's Chaos (excerpt) （頁面存檔備份，存於網際網路檔案館）
• Systems Analysis, Modelling and Prediction Group at the University of Oxford
• A page about the Mackey-Glass equation
• High Anxieties — The Mathematics of Chaos （頁面存檔備份，存於網際網路檔案館） (2008) BBC documentary directed by David Malone
• The chaos theory of evolution （頁面存檔備份，存於網際網路檔案館） - article published in Newscientist featuring similarities of evolution and non-linear systems including fractal nature of life and chaos.
• Jos Leys, Étienne Ghys et Aurélien Alvarez, Chaos, A Mathematical Adventure （頁面存檔備份，存於網際網路檔案館）. Nine films about dynamical systems, the butterfly effect and chaos theory, intended for a wide audience.