歐拉數 名稱 納皮爾常數 種類 無理數 超越數 發現 雅各布·伯努利 符號
e
{\displaystyle e}
位數 數列編號 A001113 定義
e
=
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
e
=
lim
t
→
0
(
1
+
t
)
1
t
{\displaystyle e=\lim _{t\to 0}(1+t)^{\frac {1}{t}}}
連分數 [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12...] 以此為根 的多項式或函數
∫
1
x
d
t
t
=
1
{\displaystyle \int _{1}^{x}{\frac {\mathrm {d} t}{t}}=1}
值
e
≈
{\displaystyle e\approx }
無窮級數
e
=
∑
n
=
0
∞
1
n
!
{\displaystyle e=\sum \limits _{n=0}^{\infty }{\frac {1}{n!}}}
二進制 10.10110111 1110 0001 0101 0001 … [ 1] 八進制 2.55760521 3050 5355 1246 5277 … [ 2] 十進制 2.71828182 8459 0452 3536 0287 … 十二進制 2.87523606 9821 9BA7 1971 009B … [ 3] 十六進制 2.B7E15162 8AED 2A6A BF71 5880 … [ 4] 六十進制 2;43,5,48,52,29,48,35,6,46,19,55…
e
{\displaystyle e}
x
=
0
{\displaystyle x=0}
f
(
x
)
=
a
x
{\displaystyle f(x)=a^{x}}
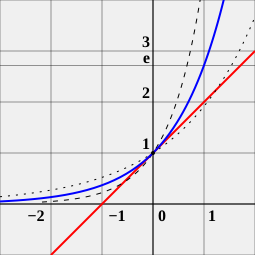
導數 (切線的斜率 )值為1之
a
{\displaystyle a}
2
x
{\displaystyle 2^{x}}
4
x
{\displaystyle 4^{x}}
y -截距為1的直線(紅色)並不相切。
e
{\displaystyle e}
自然常數 、自然底數 ,或是歐拉數 (Euler's number ),是無理數 的數學常數 ,以瑞士數學家歐拉 命名;還有個較少見的名字納皮爾常數 ,用來紀念蘇格蘭 數學家約翰·納皮爾 引進對數 。它是一個無盡不循環小數,數值約是(小數點後20位,A001113
e
=
2.71828182845904523536
⋯
{\displaystyle e=2.71828182845904523536\cdots }
271801
99990
{\displaystyle {\frac {271801}{99990}}}
有許多的函數都和
e
{\displaystyle e}
自然對數函數 的底數 即為
e
{\displaystyle e}
指數函數 也常是指以
e
{\displaystyle e}
約翰·納皮爾於1618年出版的對數 著作附錄中的一張表中第一次提到常數
e
{\displaystyle e}
常數 ,只有由它為底計算出的一張自然對數列表,通常認為這是由威廉·奧特雷德 製作的。第一次把
e
{\displaystyle e}
雅各布·伯努利 ,他嘗試計算下式的值:
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
上式代表把1與無窮小 相加,再自乘無窮 多次。
已知的第一次用到常數
e
{\displaystyle e}
萊布尼茨 於1690年和1691年給惠更斯 的通信,以
b
{\displaystyle b}
歐拉 開始用
e
{\displaystyle e}
e
{\displaystyle e}
Mechanica
c
{\displaystyle c}
e
{\displaystyle e}
用
e
{\displaystyle e}
e
{\displaystyle e}
指數函數 (exponential )一字的首字母。另一看法則稱
a
,
b
,
c
,
d
{\displaystyle a,b,c,d}
e
{\displaystyle e}
就像圓周率
π
{\displaystyle \pi }
虛數單位i ,
e
{\displaystyle e}
定義
e
{\displaystyle e}
極限 值:
e
=
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
e
=
lim
t
→
0
(
1
+
t
)
1
t
{\displaystyle e=\lim _{t\to 0}(1+t)^{\frac {1}{t}}}
定義
e
{\displaystyle e}
階乘倒數 之無窮級數 的和[ 5]
e
=
∑
n
=
0
∞
1
n
!
=
1
0
!
+
1
1
!
+
1
2
!
+
1
3
!
+
1
4
!
+
⋯
{\displaystyle e=\sum _{n=0}^{\infty }{1 \over n!}={1 \over 0!}+{1 \over 1!}+{1 \over 2!}+{1 \over 3!}+{1 \over 4!}+\cdots }
其中
n
!
{\displaystyle n!}
n
{\displaystyle n}
階乘 。
定義
e
{\displaystyle e}
x
{\displaystyle x}
∫
1
x
d
t
t
=
1
{\displaystyle \int _{1}^{x}{\frac {\mathrm {d} t}{t}}=1}
定義
e
{\displaystyle e}
x
{\displaystyle x}
lim
h
→
0
x
h
−
1
h
=
1
{\displaystyle \lim _{h\to 0}{\frac {x^{h}-1}{h}}=1}
這些定義可證明是等價的,請參見文章指數函數的特徵描述
x
x
{\displaystyle {\sqrt[{x}]{x}}}
x
=
e
{\displaystyle x=e}
很多增長或衰減過程都可以用指數函數模擬。指數函數
e
x
{\displaystyle e^{x}}
x
↦
k
e
x
{\displaystyle x\mapsto ke^{x}}
k
{\displaystyle k}
導數 相等。即:
d
d
x
e
x
=
e
x
{\displaystyle {\frac {d}{dx}}e^{x}=e^{x}}
e
x
{\displaystyle e^{x}}
泰勒級數 為
e
x
=
∑
n
=
0
∞
x
n
n
!
∀
x
{\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\quad \forall x}
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
.
.
.
{\displaystyle =1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+...}
x
{\displaystyle x}
sin
x
{\displaystyle \sin x}
cos
x
{\displaystyle \cos x}
歐拉公式 的重要等式:
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{\mathrm {i} x}=\cos x+{\rm {i}}\sin x}
當
x
=
π
{\displaystyle x=\pi }
歐拉恆等式 :
e
i
π
+
1
=
0
{\displaystyle e^{\mathrm {i} \pi }+1=0}
此式被理查德·費曼 稱為「歐拉的寶石」。
(
cos
x
+
i
sin
x
)
n
=
(
e
i
x
)
n
=
e
i
n
x
=
cos
(
n
x
)
+
i
sin
(
n
x
)
{\displaystyle (\cos x+i\sin x)^{n}=\left(e^{ix}\right)^{n}=e^{inx}=\cos(nx)+i\sin(nx)}
即狄默夫公式 。
e
{\displaystyle e}
無理數 和超越數 (見林德曼-魏爾斯特拉斯定理 )。這是第一個獲證為超越數的數,而非故意構造的(比較劉維爾數 );由夏爾·埃爾米特 (Charles Hermite )於1873年證明。有猜想它為正規數 。當
x
=
e
{\displaystyle x=e}
f
(
x
)
=
x
x
{\displaystyle f(x)={\sqrt[{x}]{x}}}
e
{\displaystyle e}
連分數 展開式有個有趣的模式,可以表示如下(A003417
e
=
[
2
;
1
,
2
,
1
,
1
,
4
,
1
,
1
,
6
,
1
,
1
,
8
,
1
,
1
,
10
,
1
,
1
,
12
,
…
]
{\displaystyle e=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,\ldots ]}
就像以下的展開式:
e
=
2
+
1
1
+
1
2
+
1
1
+
1
1
+
1
4
+
1
1
+
1
1
+
1
6
+
1
1
+
⋱
{\displaystyle e=2+{\cfrac {1}{1+{\cfrac {1}{\mathbf {2} +{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{\mathbf {4} +{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{\mathbf {6} +{\cfrac {1}{1+\ddots }}}}}}}}}}}}}}}}}}}
證明
e
{\displaystyle e}
反證法 。假設
e
{\displaystyle e}
有理數 ,則可以表示成
a
b
{\displaystyle {\frac {a}{b}}}
a
,
b
{\displaystyle a,b}
e
{\displaystyle e}
考慮數字
x
=
b
!
(
e
−
∑
i
=
0
b
1
i
!
)
{\displaystyle x=b!\left(e-\sum _{i=0}^{b}{1 \over i!}\right)}
以下將推導出
x
{\displaystyle x}
e
{\displaystyle e}
x
{\displaystyle x}
0
<
x
=
b
!
(
e
−
∑
i
=
0
b
1
i
!
)
=
b
!
(
a
b
−
∑
i
=
0
b
1
i
!
)
{\displaystyle 0<x=b!\left(e-\sum _{i=0}^{b}{1 \over i!}\right)=b!\left({a \over b}-\sum _{i=0}^{b}{1 \over i!}\right)}
=
a
(
b
−
1
)
!
−
∑
i
=
0
b
b
!
i
!
{\displaystyle =a(b-1)!-\sum _{i=0}^{b}{b! \over i!}}
=
a
(
b
−
1
)
!
−
[
1
+
∑
n
=
0
b
−
1
b
(
b
−
1
)
⋯
(
n
+
1
)
]
{\displaystyle =a(b-1)!-\left[1+\sum _{n=0}^{b-1}b(b-1)\cdots (n+1)\right]}
x
{\displaystyle x}
0
<
x
=
b
!
∑
n
=
b
+
1
∞
1
n
!
{\displaystyle 0<x=b!\sum _{n=b+1}^{\infty }{1 \over n!}}
=
1
b
+
1
+
1
(
b
+
1
)
(
b
+
2
)
+
1
(
b
+
1
)
(
b
+
2
)
(
b
+
3
)
+
⋯
{\displaystyle ={\frac {1}{b+1}}+{\frac {1}{(b+1)(b+2)}}+{\frac {1}{(b+1)(b+2)(b+3)}}+\cdots }
<
1
b
+
1
+
1
(
b
+
1
)
2
+
1
(
b
+
1
)
3
+
⋯
=
1
b
≤
1
{\displaystyle <{\frac {1}{b+1}}+{\frac {1}{(b+1)^{2}}}+{\frac {1}{(b+1)^{3}}}+\cdots ={1 \over b}\leq 1}
但是0與1之間(不含0與1)不存在有整數,故原先假設矛盾,得出
e
{\displaystyle e}
視
n
{\displaystyle n}
二項式定理 可證出:
e
=
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
=
lim
n
→
∞
∑
i
=
0
n
C
i
n
1
n
−
i
(
1
n
)
i
{\displaystyle =\lim _{n\to \infty }\sum _{i=0}^{n}C_{i}^{n}1^{n-i}\left({\frac {1}{n}}\right)^{i}}
=
lim
n
→
∞
[
C
0
n
1
n
(
1
n
)
0
+
C
1
n
1
n
−
1
(
1
n
)
1
+
C
2
n
1
n
−
2
(
1
n
)
2
+
C
3
n
1
n
−
3
(
1
n
)
3
+
.
.
.
+
C
n
n
1
0
(
1
n
)
n
]
{\displaystyle =\lim _{n\to \infty }\left[C_{0}^{n}1^{n}\left({\frac {1}{n}}\right)^{0}+C_{1}^{n}1^{n-1}\left({\frac {1}{n}}\right)^{1}+C_{2}^{n}1^{n-2}\left({\frac {1}{n}}\right)^{2}+C_{3}^{n}1^{n-3}\left({\frac {1}{n}}\right)^{3}+...+C_{n}^{n}1^{0}\left({\frac {1}{n}}\right)^{n}\right]}
=
lim
n
→
∞
[
1
×
1
+
n
×
1
n
+
n
!
(
n
−
2
)
!
2
!
×
1
n
2
+
n
!
(
n
−
3
)
!
3
!
×
1
n
3
+
.
.
.
+
1
×
1
n
n
]
{\displaystyle =\lim _{n\to \infty }\left[1\times 1+n\times {\frac {1}{n}}+{\frac {n!}{\left(n-2\right)!2!}}\times {\frac {1}{n^{2}}}+{\frac {n!}{\left(n-3\right)!3!}}\times {\frac {1}{n^{3}}}+...+1\times {\frac {1}{n^{n}}}\right]}
=
lim
n
→
∞
[
1
+
1
+
n
×
(
n
−
1
)
2
n
2
+
n
×
(
n
−
1
)
(
n
−
2
)
3
×
2
n
3
+
.
.
.
+
1
n
n
]
{\displaystyle =\lim _{n\to \infty }\left[1+1+{\frac {n\times \left(n-1\right)}{2n^{2}}}+{\frac {n\times \left(n-1\right)\left(n-2\right)}{3\times 2n^{3}}}+...+{\frac {1}{n^{n}}}\right]}
=
2
+
1
2
+
1
6
+
.
.
.
{\displaystyle =2+{\frac {1}{2}}+{\frac {1}{6}}+...}
=
2.71828...
{\displaystyle =2.71828...}
e
{\displaystyle e}
[ 6] [ 7]
日期
位數
計算者
1748年
18
李昂哈德·歐拉
1853年
137
William Shanks
1871年
205
William Shanks
1884年
346
J. M. Boorman
1946年
808
?
1949年
2,010
約翰·馮·諾伊曼
1961年
100,265
Daniel Shanks & 約翰·威廉·倫奇
1978年
116,000
史蒂芬·蓋瑞·沃茲尼克
1994年
10,000,000
Robert Nemiroff & Jerry Bonnell
1997年5月
18,199,978
Patrick Demichel
1997年8月
20,000,000
Birger Seifert
1997年9月
50,000,817
Patrick Demichel
1999年2月
200,000,579
Sebastian Wedeniwski
1999年10月
869,894,101
Sebastian Wedeniwski
1999年11月21日
1,250,000,000
Xavier Gourdon
2000年7月10日
2,147,483,648
近藤茂、Xavier Gourdon
2000年7月16日
3,221,225,472
Colin Martin、Xavier Gourdon
2000年8月2日
6,442,450,944
近藤茂、Xavier Gourdon
2000年8月16日
12,884,901,000
近藤茂、Xavier Gourdon
2003年8月21日
25,100,000,000
近藤茂、Xavier Gourdon
2003年9月18日
50,100,000,000
近藤茂、Xavier Gourdon
2007年4月27日
100,000,000,000
近藤茂、Steve Pagliarulo
2009年5月6日
200,000,000,000
近藤茂、Steve Pagliarulo
2010年2月21日
500,000,000,000
余智恆(Alexander J. Yee)
2010年7月5日
1,000,000,000,000
近藤茂、余智恆(Alexander J. Yee)
2014年11月15日
1,048,576,000,000
David Galilei Natale
在Google 2004年的首次公開募股 ,集資額不是通常的整頭數,而是$2,718,281,828,這當然是取最接近整數的
e
{\displaystyle e}
美元 。Google2005年的一次公開募股中,集資額是$14,159,265,與圓周率 有關。
Google 也是首先在矽谷 心臟地帶,接着在麻薩諸塞州劍橋 出現的神祕廣告版 的幕後黑手,它寫着{first 10-digit prime found in consecutive digits of e }.com(在
e
{\displaystyle e}
e
{\displaystyle e}
著名電腦科學家 高德納 的軟件Metafont 的軟件版本號 趨向
e
{\displaystyle e}
TeX 的軟件版本號 號是趨向於圓周率 的。
^ Sloane, N.J.A. (編). Sequence A004593 (Expansion of e in base 2) . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. ^ Sloane, N.J.A. (編). Sequence A004599 (Expansion of e in base 8) . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. ^ Sloane, N.J.A. (編). Sequence A027606 (e in duodecimal) . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. ^ Sloane, N.J.A. (編). Sequence A170873 (Hexadecimal expansion of e) . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation. ^ Iwanami Sūgaku Jiten Fourth, Tokyo: Iwanami Shoten, 2007, ISBN 978-4-00-080309-0MR 2383190 (日語) ^ Sebah, P. and Gourdon, X.; The constant e and its computation (頁面存檔備份 ,存於互聯網檔案館 )
^ Gourdon, X.; Reported large computations with PiFast (頁面存檔備份 ,存於互聯網檔案館 )

![]() A001113):
A001113):

 A003417)
A003417)






















![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)




![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)


























![{\displaystyle {\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)













![{\displaystyle f(x)={\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15600c8e263f973cca6db5347531ea5a6846aa8)
![{\displaystyle e=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e94ecd473e624ec85a2cdbb812f790ec6190a808)






![{\displaystyle =a(b-1)!-\left[1+\sum _{n=0}^{b-1}b(b-1)\cdots (n+1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/820ff0585229915ca21e10b332a06867534d8c1c)




![{\displaystyle =\lim _{n\to \infty }\left[C_{0}^{n}1^{n}\left({\frac {1}{n}}\right)^{0}+C_{1}^{n}1^{n-1}\left({\frac {1}{n}}\right)^{1}+C_{2}^{n}1^{n-2}\left({\frac {1}{n}}\right)^{2}+C_{3}^{n}1^{n-3}\left({\frac {1}{n}}\right)^{3}+...+C_{n}^{n}1^{0}\left({\frac {1}{n}}\right)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d351468fdf3864b2df828c5c7d3407a9e67c07b)
![{\displaystyle =\lim _{n\to \infty }\left[1\times 1+n\times {\frac {1}{n}}+{\frac {n!}{\left(n-2\right)!2!}}\times {\frac {1}{n^{2}}}+{\frac {n!}{\left(n-3\right)!3!}}\times {\frac {1}{n^{3}}}+...+1\times {\frac {1}{n^{n}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c4d9e899465cbda1b9cbb63a4e1635a0ce9d60c)
![{\displaystyle =\lim _{n\to \infty }\left[1+1+{\frac {n\times \left(n-1\right)}{2n^{2}}}+{\frac {n\times \left(n-1\right)\left(n-2\right)}{3\times 2n^{3}}}+...+{\frac {1}{n^{n}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e321e779caad88c5fba2f710884e6938103536fd)


