物理學史

詹姆斯·韋伯太空望遠鏡全尺寸模型與團隊成員合影。

物理學主要是研究物質、能量及它們彼此之間的關係。它是最早形成的自然科學學科之一，如果把天文學包括在內則有可能是名副其實歷史最悠久的自然科學。最早的物理學著作是古希臘科學家亞里斯多德的《物理學》。形成物理學的元素主要來自對天文學、光學和力學的研究，而這些研究通過幾何學的方法統合在一起形成了物理學。這些方法形成於古巴比倫和古希臘時期，當時的代表人物如數學家阿基米德和天文學家托勒密；隨後這些學說被傳入阿拉伯世界，並被當時的阿拉伯科學家海什木等人發展為更具有物理性和實驗性的傳統學說；最終這些學說傳入了西歐，首先研究這些內容的學者代表人物是羅吉爾·培根。然而在當時的西方世界，哲學家們普遍認為這些學說在本質上是技術性的，從而一般沒有察覺到它們所描述的內容反映著自然界中重要的哲學意義。而在古代中國和印度的科學史上，類似的研究數學的方法也在發展中。

在這一時代，包含著所謂「自然哲學」（即物理學）的哲學所集中研究的問題是，在基於亞里斯多德學說的前提下試圖對自然界中的現象發展出解釋的手段（而不僅僅是描述性的）。根據亞里斯多德的學說以及其後的經院哲學，物體運動是因為運動是物體的基本自然屬性之一。天體的運動軌跡是正圓的，這是因為完美的圓軌道運動被認為是神聖的天球領域中的物體運動的內在屬性。衝力理論作為慣性與動量概念的原始祖先，同樣來自於這些哲學傳統，並在中世紀時由當時的哲學家菲洛彭洛斯、伊本·西那、布里丹等人發展。而古代中國和印度的物理傳統也是具有高度的哲學性的。

更多資訊：天文學史和亞里斯多德物理學

古代歷史

更多資訊：天文學史

最初作為物理學的要素，主要來自天文學、光學、力學領域的知識，並藉由幾何研究以統一它們的研究方法。在古代，這些數學知識源自巴比倫人以及古希臘作家，例如阿基米德以及托勒密。同時，古代哲學——包括所謂的「物理學」——致力於藉由像亞里斯多德的四因說一類的點子來解釋自然。

古希臘

更多資訊：亞里斯多德物理學

亞里斯多德
（西元前 384–322）

自希臘遠古時期（西元前 650–480 年），前蘇格拉底哲學家逐漸理性地認識自然。 其中，名為米利都的泰勒斯的哲學家，因為他拒絕以各種超自然，宗教或神話的方式解釋自然現象，所以人們稱他為科學之祖。此外，泰勒斯宣稱每個事件皆有僅需訴諸自然的原因。西元前 580 年，泰勒斯貢獻良多，他推測水應是第一因，作磁鐵與琥珀的吸引實驗，並且形式化史上第一筆的天文學知識。作為史上首位提出演化思想而聞名的人，阿那克西曼德，並不同意泰勒斯的「水是萬物之源」觀點。他主張無窮才是萬物的基石。大約於西元前 500 年，赫拉克利特主張只有少數幾個掌控宇宙的基本定律才是萬物變化的原理，並且，任何事物隨時都在變化；沒有事物能永恆地維持在相同狀態中。早期的哲學家，留基伯（全盛時期：西元前五世紀）堅決反對神、上帝藉由天意來影響自然現象，並主張任何自然現象都是必然的。留基伯與他的學生，德謨克利特，為史上首先提出原子論的人，主張任何一切物質皆由各種不可分割、不滅的稱作原子的元素所組成。

在古典希臘時期以及希臘化時代，亞里斯多德寫下史上第一本被稱作物理學的書，日後成為著名的亞里斯多德物理學，他企圖藉由四元素解釋物體的運動（以及落體現象）。亞里斯多德相信，所有物質都由以太，或另外的四元素所組成：土、水、風、火。根據亞里斯多德，這四個陸地上的元素能夠相互轉換，並且朝向它們各自的自然位置移動。因此，石頭往宇宙中心墜落，但火總是往地球外圍靠近。

古典物理學

古典物理學指的是不涉及到量子力學或相對論的物理學，例如，牛頓力學、熱力學、馬克士威電磁學等等。

力學的發展史

約翰內斯·克卜勒

力學的歷史背景

力學是最原始的物理學分支之一，而最原始的力學則是靜力學。靜力學源於人類文明初期生產勞動中所使用的簡單機械，如槓桿、滑輪、斜面等。古希臘人從大量的經驗中了解到一些與靜力學相關的基本概念和原理，如槓桿原理和阿基米德定律。從1609至1619年期間，天文學家約翰內斯·克卜勒先後發現克卜勒行星運動三大定律，準確估算出從天文觀測獲得的行星繞著太陽的公轉數據，總結了老師第谷·布拉赫畢生的觀測數據。對宇宙中天體的觀測也成為了人類進一步研究力學運動的絕佳領域。

伽利略的動力學

伽利略·伽利萊

在17世紀的歐洲，自然哲學家逐漸展開了一場針對中世紀經院哲學的進攻，他們持有的觀點是，從力學和天文學研究抽象出的數學模型將適用於描述整個宇宙中的運動。被譽為「現代自然科學之父」的義大利（或按當時地理為托斯卡納大公國）物理學家、數學家、天文學家伽利略·伽利萊就是這場轉變中的領軍人物。伽利略所處的時代正值思想活躍的文藝復興之後，在此之前李奧納多·達文西所進行的物理實驗、尼古拉斯·哥白尼的日心說以及弗朗西斯·培根提出的注重實驗經驗的科學方法論都是促使伽利略深入研究自然科學的重要因素，哥白尼的日心說更是直接推動了伽利略試圖用數學對宇宙中天體的運動進行描述。伽利略意識到這種數學性描述的哲學價值，他注意到哥白尼對太陽、地球、月球和其他行星的運動所作的研究工作，並認為這些在當時看來相當激進的分析將有可能被用來證明經院哲學家們對自然界的描述與實際情形不符。伽利略進行了一系列力學實驗闡述了他關於運動的一系列觀點，包括藉助斜面實驗和自由落體實驗批駁了亞里斯多德認為落體速度和重量成正比的觀點，還總結出了自由落體的距離與時間平方成正比的關係，以及著名的斜面理想實驗來思考運動的問題。他在1632年出版的著作《關於托勒密和哥白尼兩大世界體系的對話》中提到：「只要斜面延伸下去，球將無限地繼續運動，而且不斷加速，因為此乃運動著的重物的本質。」。伽利略在天文學上最著名的貢獻是於1609年改良了折射望遠鏡，並藉此發現了木星的四顆衛星、太陽黑子以及金星類似於月球的相。

牛頓三大定律和萬有引力定律

艾薩克·牛頓

1687年，英格蘭物理學家、數學家、天文學家、自然哲學家艾薩克·牛頓出版了《自然哲學的數學原理》一書，這部里程碑式的著作標誌著古典力學體系的正式建立。牛頓在人類歷史上首次用一組普適性的基礎數學原理——牛頓三大運動定律和萬有引力定律——來描述宇宙間所有物體的運動。牛頓放棄了物體的運動軌跡是自然本性的觀點（例如克卜勒認為行星運動軌道本性就是橢圓的），相反，他指出，任何現在可觀測到的運動、以及任何未來將發生的運動，都能夠通過它們已知的運動狀態、物體質量和外加作用力並使用相應原理進行數學推導計算得出。

伽利略、笛卡爾的動力學研究（「地上的」力學），以及克卜勒和法國天文學家伊斯梅爾·布里阿德在天文學領域的研究（「天上的」力學）都影響著牛頓對自然科學的研究。（布里阿德曾特別指出從太陽發出到行星的作用力應當與距離成平方反比關係，雖然他本人並不認為這種力真的存在）。1673年惠更斯獨立提出了圓周運動的離心力公式（牛頓在1665年曾用數學手段得到類似公式），這使得在當時科學家能夠普遍從克卜勒第三定律推導出平方反比律。羅伯特·虎克、愛德蒙·哈雷等人由此考慮了在平方反比力場中物體運動軌道的形狀，1684年哈雷向牛頓請教了這個問題，牛頓隨後在一篇9頁的論文（後世普遍稱作《論運動》）中做了解答。在這篇論文中牛頓討論了在有心平方反比力場中物體的運動，並推導出了克卜勒行星運動三定律。其後牛頓發表了他的第二篇論文《論物體的運動》，在這篇論文中他闡述了慣性定律，並詳細討論了重力與質量成正比、與距離平方成反比的性質以及重力在全宇宙中的普遍性。這些理論最終都匯總到牛頓在1687年出版的《原理》一書中，牛頓在書中列出了公理形式的三大運動定律和導出的六個推論（推論1、2描述了力的合成和分解、運動疊加原理；推論3、4描述了動量守恆定律；推論5、6描述了伽利略相對性原理）。由此，牛頓統一了「天上的」和「地上的」力學，建立了基於三大運動定律的力學體系。

牛頓的原理（不包括他的數學處理方法）引起了歐洲大陸哲學家們的爭議，他們認為牛頓的理論對物體運動和重力缺乏一個形上學的解釋從而是不可接受的。從1700年左右開始，大陸哲學和英國傳統哲學之間產生的矛盾開始升級，裂痕開始增大，這主要是根源於牛頓與萊布尼茲各自的追隨者就誰最先發展了微積分所展開的唇槍舌戰。起初萊布尼茲的學說在歐洲大陸更占上風（在當時的歐洲，除了英國以外，其他地方都主要使用萊布尼茲的微積分符號），而牛頓個人則一直為重力缺乏一個哲學意義的解釋而困擾，但他在筆記中堅持認為不再需要附加任何東西就可以推論出重力的實在性。十八世紀之後，大陸的自然哲學家逐漸接受了牛頓的這種觀點，對於用數學描述的運動，開始放棄作出本體論的形上學解釋。

牛頓的絕對時空觀

牛頓的理論體系是建立在他的絕對時間和絕對空間的假設之上的，牛頓對時間和空間有著如下的理解：

• 絕對的、真正的和數學的時間自身在流逝著，而且由於其本性而在均勻地、與任何外界事物無關地流逝著。
• 絕對空間，就其本性而言，是與外界任何事物無關而永遠是相同的和不動的。
  — 牛頓， 自然哲學的數學原理

牛頓從絕對時空的假設進一步定義了「絕對運動」和「絕對靜止」的概念，為了證明絕對運動的存在性，牛頓還在1689年構思了一個理想實驗，即著名的水桶實驗。在水桶實驗中，一個注水的水桶起初保持靜止。當它開始發生轉動時，水桶中的水最初仍保持靜止，但隨後也會隨著水桶一起轉動，於是可以看到水漸漸地脫離其中心而沿桶壁上升形成凹狀，直到最後和水桶的轉速一致，水面相對靜止。牛頓認為水面的升高顯示了水脫離轉軸的傾向，這種傾向不依賴於水相對周圍物體的任何移動。牛頓的絕對時空觀作為他理論體系的基礎假設，卻在其後的兩百年間倍受質疑。特別是到了十九世紀末，奧地利物理學家恩斯特·馬赫在他的《力學史評》中對牛頓的絕對時空觀做出了尖銳的批判。

熱學的發展史

詹姆斯·焦耳

熱功當量和熱力學第一定律

熱學起源於人們對熱現象的概念和本性的研究，熱和溫度的概念是在伽利略發明了溫度計之後逐漸理清的。而人們最初對熱的本性的認知可以用所謂「熱質說」來概括，即熱是一種會從高溫物體流向低溫物體的物質，同時根據實驗結果，熱這種物質沒有質量，它被稱作「卡路里」。熱質說能解釋很多熱現象，但到了十八世紀末，英國的倫福德伯爵在慕尼黑兵工廠領導鑽制大炮的工作時，發現「銅炮在鑽了很短一段時間後就會發生大量的熱；而被鑽頭從炮上鑽出來的銅屑更熱（像我用實驗所證實的，發現它們比沸水還要熱）。」倫福德認為「在這些實驗中由摩擦所生的熱的來源似乎是無窮無盡的」，因此他認為熱「絕不能是具體的物質」。

在當時力學的發展已經使人們對能量的轉化與守恆有了初步的理解，特別是笛卡爾的運動不滅理論和萊布尼茲的「活力守恆原理」，他認為$mv^{2}\,$這個代表「活力」的量在運動中是守恆的。德國醫生、物理學家尤利烏斯·馮·邁爾在工作中受到啟發，在1841年發表了他關於熱是機械能的一種形式的猜測，他還進一步將這個理論推廣到不同形式能量之間的轉化中，歸納出能量的守恆性。他的陳述「能量既不能被產生也不能被消滅」在今天被看作是熱力學第一定律最早的表述形式之一。而與此同時，英國實驗物理學家、釀酒師詹姆斯·焦耳則從實驗上驗證了熱是能量的一種形式的猜想，並在1843年給出了熱功當量的實驗測得值。德國物理學家赫爾曼·馮·亥姆霍茲同樣從「活力守恆原理」出發，進而將能量的轉化與守恆推廣到機械運動以外的各種過程中，這些研究成果發表在1847年的論文《力的守恆》中。

在這些理論和實驗研究的基礎上，德國物理學家魯道夫·克勞修斯於1850年給出了熱力學第一定律的數學形式，其後這一定律在英國物理學家克耳文勳爵等人的修訂下成為物理學中的一條基本定律。

魯道夫·克勞修斯

熱機效率和熱力學第二定律

熱力學第二定律的建立起源於人們試圖提升熱機效率的探索。法國物理學家、工程學家尼古拉·卡諾研究了一個由兩個等溫過程和兩個絕熱過程組成的理想可逆熱力學循環（卡諾循環），並得出結論：「熱機的效率只與兩個熱源的溫差有關，而與熱機的工質無關。任何熱機的效率都不能高於可逆熱機的效率。」卡諾的結論被看作是熱力學第二定律的前身，這一成果後來被克耳文採用，利用卡諾熱機只與溫差有關而與工質無關的特性建立了絕對溫標。

克勞修斯在研究卡諾循環中發現，在循環中有一部分熱量能轉化成機械能，而大部分熱量則是從高溫熱源傳遞到低溫熱源，這兩部分熱量和產生的功有著確定的關係。他在1850年發表了《論熱的移動力及可能由此得出的熱定律》，重新闡述了卡諾定理，並在1854年的另一篇論文中進一步表述了熱力學第二定律：

熱永遠不能從冷的物體傳向熱的物體，如果沒有與之聯繫的、同時發生的其它的變化的話。
— 魯道夫·克勞修斯， 熱的機械論中第二個基本理論的另一形式

在此時克勞修斯還引入了熵的概念，在他的論文《熱的動力理論的基本方程式的幾種方便形式》中指出，對可逆過程熵增只能為零，對不可逆過程熵增總是正值。他後來用熵的概念對熱力學第二定律重新做了表述，其數學表達式為$\int {\frac {\delta Q}{T}}\geq 0$。但直到1865年，克勞修斯才真正將${\frac {\delta Q}{T}}$這個量稱作熵。按克勞修斯的說法，科學上如此重要的一個量應取自古希臘語，因此他選擇了ητροπη，意為「轉變」來為之命名。

詹姆斯·馬克士威

分子運動論

最早嘗試建立分子運動論的人是瑞士數學家歐拉，他於1729年曾假設空氣由大量旋轉的球形分子構成，並且在任意溫度下分子速率都相同。從這個假設出發他推導出氣體壓力和密度成正比，也就相當於在理論上證明了波以耳定律。而荷蘭-瑞士物理學家丹尼爾·白努利在1738年出版的《水力學》一書中，認為氣體中存在大量沿不同方向運動的分子，這些分子對容器表面的衝擊效應構成了宏觀上的氣體壓力，他同樣從分子運動得到了更具普遍意義的壓力公式。然而這些觀點在當時並未被接受，原因之一是在當時能量的轉化與守恆定律還沒有廣為人知。這種情況一直持續到1856年，德國化學家奧古斯特·克羅尼格創建了一個簡單的氣體分子平動模型，由此可以導出理想氣體狀態方程式。

1857年，克勞修斯在獨立於克里尼希理論的情況下，用自己的語言建立了一個相似但更為複雜的分子運動理論，這裡不但考慮了氣體分子的平動，同時還考慮了轉動和振動。在這一理論中克勞修斯引入了研究分子運動論的統計思想，建立了氣體分子的平均自由徑這一概念。不過，克勞修斯的理論只是使用了分子的平均速率，沒有考慮到實際氣體分子的速率實則呈現出一個分布函數。1859年，英國物理學家詹姆斯·馬克士威在閱讀了克勞修斯的論文後，在論文《氣體動力理論的說明》一文中建立了氣體分子速率的馬克士威分布，這一分布函數描述了在特定速率範圍內分子數量所占比例。這一定律是物理學中第一個基於統計規律的物理定律。

路德維希·波茲曼

統計力學的建立

在馬克士威發表分子速率分布理論之後，奧地利物理學家路德維希·波茲曼受其啟發開始了對分子運動論的研究。他指出分子運動理論必須依靠統計手段來建立，並通過修訂馬克士威分布於1871年得到了氣體分子在勢場中的速率分布函數，這被稱作波茲曼分布或馬克士威-波茲曼分布，是古典統計力學中最基本的分布函數。1872年，波茲曼在論文《氣體分子熱平衡的進一步研究》中證明，非馬克士威分布的氣體分子隨著時間的推移必將趨向馬克士威分布，這也就是所謂H定理，是熵增原理在非平衡態下的推廣。H定理指出了過程的方向性，從而引出了所謂「可逆性悖論」的爭議：微觀上分子的碰撞是可逆的，為何宏觀上的整體效果卻是不可逆的？波茲曼針對這個問題研究了熱力學第二定律的統計詮釋：他指出如果能把所有分子的微觀運動同時反向，則確實可以回到初始狀態；然而在實際中這種可能性幾乎為零，絕大多數狀態都是平衡態，因此在宏觀統計規律上表現為熵總是增加的。也就是說，熱力學第二定律是一條機率的定律，它的結論不能由一條動力學方程式來檢驗。波茲曼證明了熵和系統的熱力學機率的自然對數成正比，這成為了波茲曼熵的定義。熱力學第二定律在統計詮釋下可表述為：「孤立系統的熵對應著系統分子的熱力學機率，並總是趨向最大值。」

在馬克士威和波茲曼引入統計詮釋之前，熱力學始終是基於一組唯象學定律基礎之上的。美國物理學家約西亞·吉布斯在馬克士威和波茲曼思想的基礎上建立了統計力學，從而能夠用力學定律和統計方法來從本質上精確描述熱力學定律。吉布斯的統計力學引入了系綜的概念，並以劉維定理作為統計力學的基本方程式，求解熱力學巨觀量實則就是求解系綜在相空間中的機率分布（配分函數）。統計力學通過統計詮釋建立了熱力學定律與分子運動論之間的內在聯繫，至此成為物理學中又一個完備的理論體系。

電磁學的發展史

電學史

主條目：電學史

威廉·吉爾伯特

靜電和靜磁現象很早就被人類發現，由於摩擦起電現象，英語中「電」的語源為希臘語「琥珀」一詞。然而直到1600年，由於威廉·吉爾伯特的嚴謹治學態度，才開始對於電與磁的現象出現系統性研究。吉爾伯特是英國女王伊莉莎白一世的皇家醫生，他對於電和磁情有獨鍾，撰寫了第一本闡述電和磁的科學著作《論磁石》，其中，他指出，琥珀不是唯一可以經過摩擦產生靜電的物質，鑽石、藍寶石、玻璃等等，也都可以演示出同樣的電學性質，這論述成功地摧毀了一個持續了2000年的錯誤觀念，即琥珀的吸引力是其獨特性質。吉爾伯特製成的靜電驗電器可以敏銳的探測靜電電荷，在之後的一個世紀，這是最優良的探測靜電電荷的儀器。由於在電學給出眾多重要貢獻，吉爾伯特被後人尊稱為「電學之父」。

夏爾·庫侖

庫侖定律是靜電學中的基本定律，主要描述了靜電力與電荷電量成正比，與距離的平方反比的關係。蘇格蘭物理學家約翰·羅比遜（1759年）和英國物理學家亨利·卡文迪什（1773年）等人都進行過實驗驗證了靜電力的平方反比律，然而他們的實驗卻遲遲不為人知。法國物理學家夏爾·庫侖於1784年至1785年間進行了他著名的扭秤實驗，其實驗的主要目的就是為了證實靜電力的平方反比律，因為他認為「假說的前一部分無需證明」，也就是說他已經先驗性地認為靜電力必然和萬有引力類似，和電荷電量成正比。扭秤的基本構造為：一根水平懸於細金屬絲的輕導線兩端分別置有一個帶電小球A和一個與之平衡的物體P，而在實驗中在小球A的附近放置同樣大小的帶電小球B，兩者的靜電力會在輕導線上產生扭矩，從而使輕杆轉動。通過校正懸絲上的旋鈕可以將小球調回原先位置，則此時懸絲上的扭矩等於靜電力產生的力矩。如此，兩者之間的靜電力可以通過測量這個扭矩、偏轉角度和導線長度來求得。庫侖的結論為：

……對同樣材料的金屬導線而言，扭矩的大小正比於偏轉角度和導線橫截面直徑的四次方，且反比於導線的長度……
— 夏爾·庫侖， 金屬導線扭矩和彈性的理論和實驗研究

庫侖在其後的幾年間也研究了磁偶極子之間的作用力，他也得出了磁力也具有平方反比律的結論。不過，他並未認識到靜電力和靜磁力之間有何內在聯繫，而且他一直將電力和磁力吸引和排斥的原因歸結於假想的電流體和磁流體——具有正和負區別的，類似於「熱質」一般的無質量物質。

靜電力的平方反比律確定後，很多後續工作都是同萬有引力做類比從而順理成章的結果。1813年法國數學家、物理學家西莫恩·德尼·卜瓦松指出拉普拉斯方程式也適用於靜電場，從而提出卜瓦松方程式；其他例子還包括靜電場的格林函數（喬治·格林，1828年）和高斯定理（卡爾·高斯，1839年）。

格奧爾格·歐姆

伏打電堆示意

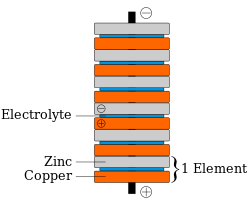
十八世紀末，義大利生理學家路易吉·伽伐尼發現蛙腿肌肉接觸金屬刀片時會發生痙攣，他其後在論文中認為生物中存在著一種所謂「神經電流」。義大利物理學家亞歷山德羅·伏打對這種觀點並不贊同，他對這種現象進行研究後認為這不過是外部電流的作用，而蛙腿肌肉只是起到了導體的連接作用。1800年，伏打將鋅片和銅片夾在用鹽水浸濕的紙片中，得到了很強的電流，這稱作伏打電堆 ；而將鋅片和銅片浸入鹽水或酸溶液中也能得到相同的效果，這稱作伏打電池。伏打電堆和電池的發明為研究穩恆電流創造了條件。

1826年，德國物理學家格奧爾格·歐姆從傅立葉對熱傳導規律的研究中受到啟發，在傅立葉的熱傳導理論中，導熱杆中兩點的熱流量正比於這兩點之間的溫度差。因而歐姆猜想電傳導與熱傳導相似，導線中兩點之間的電流也正比於這兩點間的某種驅動力（歐姆稱之為電張力，即現在所稱的電動勢）。歐姆首先嘗試用電流的熱效應來測量電流強度，但效果不甚精確，後來歐姆利用了丹麥物理學家漢斯·奧斯特發現的電流的磁效應，結合庫侖扭秤構造了一種新型的電流扭秤，讓導線和連接的磁針平行放置，當導線中通過電流時，磁針的偏轉角與導線中的電流成正比，即代表了電流的大小。歐姆測量得到的偏轉角度（相當於電流強度）與電路中的兩個物理量分別成正比和反比關係，這兩個量實際相當於電動勢和電阻。歐姆於1827年發表了他的著作《直流電路的數學研究》，明確了電路分析中電壓、電流和電阻之間的關係，極大地影響了電流理論和應用的發展，在這本書中首次提出的電學定律也因此被命名為歐姆定律。

庫侖發現了磁力和電力一樣遵守平方反比律，但他沒有進一步推測兩者的內在聯繫，然而人們在自然界中觀察到的電流的磁現象（如富蘭克林在1751年發現放電能將鋼針磁化）促使著人們不斷地探索這種聯繫。首先發現這種聯繫的人是丹麥物理學家奧斯特，他本著這種信念進行了一系列有關的實驗，最終於1820年發現接通電流的導線能對附近的磁針產生作用力，這種磁效應是沿著圍繞導線的螺旋方向分布的。

安德烈-瑪麗·安培

安培的電磁學定理

在奧斯特發現電流的磁效應之後，法國物理學家讓-巴蒂斯特·必歐和費利克斯·沙伐進一步詳細研究了載流直導線對周圍磁針的作用力，並確定其磁力大小正比於電流強度，反比於距離，方向垂直於距離連線，這一規律被歸納為著名的必歐-沙伐定律。而法國物理學家安德烈-瑪麗·安培在奧斯特的發現僅一周之後（1820年9月）就向法國科學院提交了一份更詳細的論證報告，同時還論述了兩根平行載流直導線之間磁效應產生的吸引力和排斥力。在這期間安培進行了四個實驗，分別驗證了兩根平行載流直導線之間作用力方向與電流方向的關係、磁力的向量性、確定了磁力的方向垂直於載流導體以及作用力大小與電流強度和距離的關係。安培並且在數學上對作用力進行了推導，得到了普遍的安培力公式，這一公式在形式上類似於萬有引力定律和庫侖定律。1821年，安培從電流的磁效應出發，設想了磁效應的本質正是電流產生的，從而提出了分子環流假說，認為磁體內部分子形成的環形電流就相當於一根根磁針。1826年，安培從斯托克斯定理推導得到了著名的安培環路定理，證明了磁場沿包圍產生其電流的閉合路徑的曲線積分等於其電流密度，這一定理成為了馬克士威方程組的基本方程式之一。安培的工作揭示了電磁現象的內在聯繫，將電磁學研究真正數學化，成為物理學中又一大理論體系——電動力學的基礎。

麥可·法拉第

電磁感應現象

英國物理學家麥可·法拉第早年跟隨化學家漢弗里·戴維從事化學研究，他對電磁學的貢獻還包括抗磁性的發現、電解定律和磁場的旋光性（法拉第效應）。

在奧斯特發現電流的磁效應之後的1821年，英國《哲學學報》邀請當時擔任英國皇家研究所實驗室主任的法拉第撰寫一篇電磁學的綜述，這也導致了法拉第轉向電磁領域的研究工作。法拉第考慮了奧斯特的發現，也出於他同樣認為自然界的各種力能夠相互轉化的信念，他猜想電流應當也如磁體一般，能夠在周圍感應出電流。從1824年起，法拉第進行了一系列相關實驗試圖尋找導體中的感應電流，然而始終未獲成功。直到1831年8月29日，他在實驗中發現對於兩個相鄰的線圈A和B，只有當接通或斷開線圈迴路A時，線圈B附近的磁針才會產生反應，也就是此時線圈B中產生了電流。如果維持線圈A的接通狀態，則線圈B中不會產生電流，法拉第意識到這是一種瞬態效應。一個月後，法拉第向英國皇家學會總結了他的實驗結果，他發現產生感應電流的情況包括五類：變化中的電流、變化中的磁場、運動的穩恆電流、運動的磁體和運動的導線。法拉第電磁感應定律從而表述為：任何封閉電路中感應電動勢的大小，等於穿過這一電路磁通量的變化率。不過此時的法拉第電磁感應定律仍然是一條觀察性的實驗定律，確定感應電動勢和感應電流方向的是俄國物理學家海因里希·冷次，他於1833年總結出了著名的冷次定律。法拉第定律後來被納入馬克士威的電磁場理論，從而具有了更簡潔更深刻的意義。

法拉第另一個重要的貢獻是創立了力線和場的概念，力線實際是否認了超距作用的存在，這些思想成為了馬克士威電磁場理論的基礎。愛因斯坦稱其為「物理學中引入了新的、革命性的觀念，它們打開了一條通往新的哲學觀點的道路」，意為場論的觀念是有別於舊的機械觀中以物質為主導核心的哲學觀念。

馬克士威電磁場理論

海因里希·魯道夫·赫茲

詹姆斯·馬克士威對電磁理論的貢獻是里程碑式的。馬克士威自1855年開始研究電磁學，1856年他發表了首篇專論《論法拉第力線》，其中描述了如何類比流體力學中的流線和法拉第的力線，並用自己強大的數學功底重新描述了法拉第的實驗觀測結果，這部分內容被馬克士威用六條數學定律概括。1861年至1862年間，馬克士威發表了第二篇電磁學論文《論物理力線》，在這篇論文中馬克士威嘗試了所謂「分子渦流」模型，他假設在磁場作用下的介質中存在大量排列的分子渦流，這些渦流沿磁力線旋轉，且角速度正比於磁場強度，分子渦流密度正比於介質磁導率。這一模型能很好地通過近距作用之說來解釋靜電和靜磁作用，以及變化的電場與磁場的關係。更重要的是，它預言了在電場作用下的分子渦流會產生位移，從而以位能的形式儲存在介質中，這相當於在介質中產生了電動勢，這成為了馬克士威預言位移電流存在的理論基礎。此外，將這種介質理論應用到彈性波上，可以計算求得在真空或以太中橫波的傳播速度恰好和當時已知的光速（斐索，1849年）非常接近，馬克士威由此大膽預言：

我們難以排除如下的推論：光是由引起電現象和磁現象的同一介質中的橫波組成的。
— 詹姆斯·馬克士威， 論物理力線

1865年馬克士威發表了他的第三篇論文《電磁場的動力學理論》，在論文中他堅持了電磁場是一種近距作用的觀點，指出「電磁場是包含和圍繞著處於電或磁狀態的物體的那部分空間，它可能充有任何一種物質」。在此馬克士威提出了電磁場的方程組，一共包含有20個方程式（電位移、磁場力、電流、電動勢、電彈性、電阻、自由電荷和連續性方程式）和20個變量（電磁動量、磁場強度、電動熱、傳導電流、電位移、全電流、自由電荷電量、電位）。這實際是8個方程式，但到1890年才由海因里希·魯道夫·赫茲給出了現代通用的形式，這是赫茲在考慮了阿爾伯特·邁克生在1881年的實驗（也是邁克生-莫雷實驗的先行實驗）中得到了以太漂移的零結果後對馬克士威的方程組進行的修改。1887年至1888年間，赫茲通過他製作的半波長偶極子天線成功接收到了馬克士威預言的電磁波，電磁波是相互垂直的電場和磁場在垂直於傳播方向的平面上的振動，同時赫茲還測定了電磁波的速度等於光速。赫茲實驗證實電磁波的存在是物理學理論的一個重要勝利，同時也標誌著一種基於場論的更基礎的物理學即將誕生。1931年，在馬克士威百年誕辰的紀念會上，愛因斯坦盛讚法拉第和馬克士威的工作是「牛頓力學以來物理學中最偉大的變革」。

光學的發展史

主條目：光學史

幾何光學的發展

主條目：幾何光學

克勞狄烏斯·托勒密

西方世界中最早的光學研究記載來自歐幾里德的《反射光學》（Catoptrica）；而在托勒密的著作《光學》（原作已佚）中記載了他對折射定律的研究，他在當時認為折射角正比於入射角，這個觀點後來被阿拉伯學者海什木發現有誤。海什木本人對光學有著相當的研究成果，在他的著作《光學全書》裡記載了大量他進行過的光學實驗，他研究過光的直線傳播、反射和折射、透鏡和各種反射鏡等。在折射的研究中，是他首先發明了將反射光和折射光在水平和豎直方向上分解這一幾何光學中的基本方法。他甚至得到了類似於司乃耳定律的結論，但沒有經過定量的數學推導。

克卜勒在他1611年的光學著作《折光學》中記載了他所進行的光的折射實驗，記錄表明他在實驗中曾觀察到全反射現象。1621年，荷蘭物理學家司乃耳通過進行和克卜勒相類似的實驗首次總結出了正確的折射定律，後來折射定律也常被稱作司乃耳定律。笛卡爾在他的著作《方法論》中也有關於折射的研究，他將光看作機械的彈性小球，認為小球在不同的介質中的速度是不同的，並假設平行於介質交面的光速分量始終保持不變，由此可以推出入射角與折射角的正弦的比值是定值。不過，笛卡爾的結果和事實相比需要假設光在光疏媒質中要比在光密媒質中走得慢。1661年，法國數學家皮埃爾·德·費馬將費馬原理應用於幾何光學，得到了折射定律的正確形式。費馬原理作為最小作用量原理的一個特例，應用它來證明折射定律具有物理上的正確性。

光的色散

牛頓在光學領域也做出了巨大貢獻，其中最重要的發現是光的色散。牛頓的青年時代正是望遠鏡和顯微鏡逐漸占領科學實驗觀測重要地位的時期，人們在使用這些儀器的同時卻發現成像總是帶有像差和色差等問題。因此牛頓研究光學的初衷是為了改進這些光學儀器。1666年，牛頓在參考了笛卡爾、虎克和波以耳等人的分光實驗後，把房間弄成漆黑，只讓室外的陽光透過留在窗戶上的一個小孔，陽光照射到放置的三稜鏡上，如此牛頓在對面的牆上得到了光譜。牛頓本人描述說：「當我第一次看到由此而產生的鮮明強烈的光色時，使我感到極大的愉快」。隨後牛頓還進行了其他實驗證明了色散不是光和稜鏡交互作用的結果，以及色散後的光譜能通過倒置的稜鏡再次還原為白光。通過這些實驗，牛頓總結出了幾條結論，包括不同的色光具有不同的折射率、白光是由多種色光按比例混合而成的等，並解釋了物體呈現各種顏色的原因是該物體對特定顏色的光反射更強所致。1704年，牛頓出版了《光學——關於光的反射、折射、繞射和顏色的論文》一書，集中匯總了他在光學領域所做的研究工作。

克里斯蒂安·惠更斯

光的本性

光的本性問題是物理學界長久以來一直爭論不休的一個難題。牛頓在思考這個問題時，將他所擅長的物質、粒子和力等概念滲透到光學中，從而將光的本性解釋為物質的微粒。這些微粒以一定的速率在真空中保持直線運動，碰撞到光滑的鏡面則產生彈性反射，而前文中笛卡爾的理論推導也證明了這種假說能夠解釋光的折射現象。微粒說能夠在相當程度上完整地解釋幾何光學，而對於色散的問題，則要假設每一種顏色的光對應一種顏色的微粒，不同顏色的微粒在真空中具有相同的速度，而在介質中則具有不同的速度。然而，關於光的本性很多物理學者一直持有另外一種觀點，即光是一種彈性的機械波，持這種波動觀點的代表人物有虎克和惠更斯等人。惠更斯在1678年所闡述的觀點認為，光是發光體內部的粒子振動所產生的機械波，這種機械波傳播所依靠的介質被稱作以太。惠更斯認為光是一種縱波，從而以太這種物質類似於空氣一樣，但沒有任何質量，瀰漫於整個宇宙中而無處不在。因此在波動說看來，光的本質就是能量通過以太的振動在空間中的傳遞。波動說同樣可以解釋很多光學現象，例如波在其他介質中的傳播速率要小於在以太中的傳播速率，因而這種效應會引起折射。對於色散，波動說認為每種顏色的光對應有不同的波長，因而在以太以外的其他介質中波速不同。儘管波動說能夠貌似更簡單地解釋光學現象（除去需要假設存在以太的問題），當時的科學界由於更相信牛頓的權威，在波動說提出的一百多年裡一直更推崇微粒說。

奧古斯丁·菲涅耳

這種情形一直持續到十九世紀初，1801年英國科學家托馬斯·楊成功實現了光的雙縫干涉實驗，這是對波動說的有力證明。他通過實驗還初步測定了空氣中不同色光的波長，已經接近於現代測定的精確值。1809年法國物理學家馬呂斯發現了光的偏振，為了解釋這種現象托馬斯·楊在1817年假設了光波具有一個非常小的振動的橫向分量，不過到了1821年，法國物理學家奧古斯丁·菲涅耳通過數學計算得出結論，光的振動完全是橫向的。菲涅耳對波動光學進行了理論和實驗的全方位研究，締造了波動光學的理論基礎，他的主要理論成就包括：提出了兩束光的干涉條件，在數學上完善了描述光傳播規律的惠更斯－菲涅耳原理，菲涅耳指出光波的包絡面實際是各個子波彼此干涉的結果，並描述了近場的菲涅耳繞射；菲涅耳還得到了在物理上定量描述反射和折射規律的菲涅耳方程式；以及關於光的偏振的研究，並發現了圓偏振光和橢圓偏振光。

儘管波動說在十九世紀的發展非常成功，光是一種橫波的事實意味著惠更斯關於以太的理論需要修改：以太不能像空氣那樣是「氣狀」的，而必須是彈性「膠狀」的。然而，假設一種膠狀的以太無疑會帶來更多麻煩，例如只有光才會和以太產生交互作用，而物質不會產生任何作用。正如愛因斯坦所評價的那樣，需要假設彈性膠狀的以太意味著試圖完全用力學的觀點來解釋光的本性是沒有希望的，這也正是法拉第和馬克士威提出場的概念的重要意義所在。

光譜學的發展

主條目：光譜學

約瑟夫·馮·夫琅和費

十九世紀八十年代以前，人們對光譜學的研究還僅限於對光譜的觀測。著名的測量研究包括德國物理學家約瑟夫·夫琅和費在1814年至1815年間測定的太陽光譜，他將得到的八條吸收光譜線用字母A-H標記，後人稱之為夫琅和費線。後來的光譜學主要用於新的化學元素的發現上，例如德國物理學家古斯塔夫·克希荷夫就是通過研究鹼金屬的光譜發現了新元素銫（1860年）和銣（1861年）。然而，從哪方面來看都需要對光譜的成因以及譜線之間的關係作出一個物理上的解釋，而這一點恰恰又是在當時高度依賴機械觀的物理學界無法企及的問題。相反，一名瑞士中學教師約翰·巴耳末於1884年總結出了一個經驗性的氫光譜公式，正是這個公式的正確性引發了物理學家對原子光譜進一步的探索。1890年，瑞典物理學家約翰尼斯·芮得柏在不了解巴耳末工作的情況下得到了一個更具有普遍意義的經驗公式，而巴耳末公式正是芮得柏得到的一個特例，後人並由此進一步成功預言了帕邢系的存在。然而即便如此，此時人們對光譜的理解依然是唯象的，真正在物理層面上的解釋則要等到尼爾斯·波耳的時代。

古典物理學的革命

克耳文勳爵

歷史背景

在1900年4月27日，克耳文勳爵在英國皇家研究所做了一篇名為《在熱和光動力理論上空的十九世紀烏雲》的發言，演講中克耳文聲稱：

動力學理論認為熱和光都是運動的方式，現在這一理論的優美和明晰，正被兩朵烏雲籠罩著。
— 克耳文勳爵， 在熱和光動力理論上空的十九世紀烏雲

克耳文所言的兩朵烏雲分別是指邁克生-莫雷實驗測量的零結果和黑體輻射理論出現的問題。出自對牛頓理論的高度信任，克耳文也相信這兩個問題會被最終掃清，發言中他針對這兩個問題提出了自己的解決方案。對於波動說中為何光以外的其他物質不會和「膠狀」以太發生交互作用的問題，克耳文提出假設以太是可伸縮的，從而邁克生-莫雷實驗不能完全否定以太的自由運動；而對於黑體輻射的問題，克耳文認為馬克士威、波茲曼和瑞立等人對能量均分定理永遠成立的維護是不必要的，「解決問題最簡單的途徑就是否定這一結論」。克耳文對這兩個問題的在意程度反映了當時物理學界對物理學理論體系的普遍憂慮，但他很有可能沒有想到的是，這兩朵烏雲給物理學帶來的是一場突如其來的風暴，這場風暴顛覆了舊理論體系的框架，分別導致了二十世紀物理學的兩大理論體系：相對論和量子力學的誕生。

X射線和電子的發現

威廉·倫琴

從1895年德國物理學家威廉·倫琴發現X射線開始，物理學界在短短十年間誕生出很多前所未有的研究發現，包括天然放射性（貝可勒爾，1896年）、塞曼效應（塞曼，1896年）、電子（約瑟夫·湯木生，1897年）、α和β射線（拉塞福，1898年）、放射性元素釙和鐳（居禮夫婦，1898年）、電子質量隨速度增長（沃爾特·考夫曼，1901年）等。其中X射線和電子的發現都可以追溯至人們在真空放電管內所做的真空放電實驗，這种放電現象被稱作陰極射線。1895年11月8日，時為德國維爾茨堡大學校長的倫琴在進行陰極射線的實驗時，觀察到放在射線管附近塗有氰亞鉑酸鋇的屏上發出的微光，最後他確信這是一種尚未為人所知的新射線。1895年12月28日他完成了初步的實驗報告《一種新的射線》並發表於《維爾茨堡物理醫學學會》上。為了表明這是一種新的射線，倫琴採用表示未知數的X來命名（儘管很多人建議他將其命名為倫琴射線，這後來也成為了X射線的別名）。倫琴為此獲得了首屆諾貝爾物理學獎，不過他很長時間都沒有弄清這種新射線的本質，直到1912年德國物理學家馬克斯·馮·勞厄通過晶體繞射的方法確定了X射線是一種頻率很高的電磁波，而後來英國物理學家亨利·莫色勒則指出X射線產生於原子內部內層電子的量子躍遷。

約瑟夫·湯木生

英國物理學家、劍橋大學卡文迪許實驗室的約瑟夫·湯木生自1890年起開始研究陰極射線，他在1897年重做了赫茲的實驗，但精細程度上有相當大的提高：他使用了真空度更高的放電管和更強的電場。實驗中他觀察到了電場中穩定的偏轉，並利用測量的偏轉角度計算了這種未知粒子的電荷質量比，這個測量值不依賴於電極的材料和氣體的成分。湯木生等人又測定了這種粒子所帶的電量，發現其與氫離子的帶電量相同。其後湯木生又採用類似方法研究了光電效應中的光電流和熱電發射效應中的電流，發現它們也都是由相同粒子組成的。這些事實加上法國物理學家亨利·貝可勒爾對β射線成分的研究結果，證明這種粒子普遍存在於電流中，並且是比原子更小的組成單元。湯木生採用「電子」這個名稱來稱呼這種粒子，電子是人類發現的第一個基本粒子，它的發現改變了長久以來人們認為原子不可分的傳統觀念。

以太風

阿爾伯特·邁克生

以太是光的波動說基於機械觀的論點引入的假想光波介質，同時它也是一種絕對慣性系。由於這種假想物質無處不在、絕對靜止、與光以外的物質不會發生任何可觀測的作用，而且它又是膠狀彈性的，關於以太是否真的存在一直是理論和實驗物理學界關注的問題。由於以太是絕對慣性系，地球在以太中的運動相當於在地球上形成相對地球運動的反方向的以太風，這從而成為了人們能夠想到的一種測量以太的途徑。馬克士威在《大英百科全書》的《以太》條目中提到了這種實驗方案：由於以太的運動會引起在其中傳播的光速的變化，而以太風的速度又相當於反向的地球軌道速度，則可以通過比較這兩種速度來觀察以太。然而受當時在地面上測量光速的技術所限，以太風所導致的光傳播時間變化也只能為總傳播時間的億分之一，這種精度的測量對於的當時的技術而言是非常困難的。不過到了1880年，美國物理學家阿爾伯特·邁克生製造了一種全新的高靈敏干涉儀——邁克生干涉儀，如此光速的變化將能反映到干涉的相位差中，邁克生干涉儀的靈敏度已能達到馬克士威所言的測量要求。

1881年4月邁克生在波茨坦天文台進行了上述干涉實驗，結果是干涉條紋的移動遠遠小於可能的預期，並與地球軌道運動並不相關，邁克生從而猜測絕對靜止的以太慣性系並不存在。1887年他又和愛德華·莫雷合作改進了干涉實驗，提高了實驗的穩定性和靈敏度，然而結果依然沒有變化。根據他們記錄的測量結果，即使地球和以太之間的相對運動導致了條紋位移，這種位移不會大於條紋間距的0.01倍，而假設以太存在時的理論值則會達到0.4倍。邁克生-莫雷實驗的零結果對當時的物理學界是一朵名副其實的烏雲，為了解釋這個結果同時又維護以太理論的正確性，荷蘭物理學家亨德里克·勞侖茲於1892年提出了收縮假說，並於1895年給出了著名的長度收縮公式$l=l_{0}{\sqrt {1-v^{2}/c^{2}}}\,$。這一假說不但可以解釋邁克生-莫雷實驗的零結果，也否定了任何在地球上觀察以太風的可能性。

紫外災變

古斯塔夫·克希荷夫

紫外災變這一概念的提出起源於人們對熱輻射定律的研究，或更準確的說，是從古斯塔夫·克希荷夫1859年提出黑體輻射的概念開始的。1879年，斯洛維尼亞物理學家約瑟夫·斯特凡經驗性得到黑體輻射能量正比於黑體溫度的四次方的結論，並由波茲曼於1884年從理論上證明，這被稱作斯特凡-波茲曼定律。1893年德國物理學家威廉·維因得到了描述黑體輻射的電磁波波長與黑體溫度之間反比關係的定律，即維因位移定律；而後在1896年又得到了一個描述黑體輻射能量和波長之間關係的定律，即維因近似（也叫維因輻射定律）。維因的定律引起了物理學界的注意，由於它基本上屬於基於實驗測量的經驗性公式，很多理論物理學家試圖在理論上對其進行修正。德國物理學家馬克斯·普朗克自1897年起開始進行這項工作，通過將電磁理論應用於熱輻射和諧振子的交互作用，他於1899年得到了維因輻射定律的理論版本。然而，實驗觀測表明維因近似並不適用於長波情形，在低頻區域需要進行修正。這種偏差導致了普朗克對能量進行了量子化假設，從而在1900年導出了普朗克黑體輻射定律。

真正引起紫外災變的導火索是能量均分定理。瑞立勳爵在研究黑體輻射的過程中，注意到對頻率較低的情形能量均分定理應當成立，從而假設在空腔中輻射的電磁波能量按自由度均分。這樣得到的公式符合長波情形，然而當頻率趨於無窮大時輻射的能量也因此趨於無窮大，瑞立注意到了這種情形的荒謬性並試圖對公式加以修正。1905年，詹姆斯·金斯爵士發現了瑞立公式中係數的錯誤，修正後這個公式被稱作瑞立-金斯定律，代表了能量均分定理應用於黑體輻射的結果。由於馬克士威、波茲曼和瑞立等人對能量均分定理正確性的維護，瑞立-金斯定律在紫外區域發散的情形對古典物理學而言是不可理解的，這被奧地利物理學家保羅·埃倫費斯特於1911年稱作所謂「紫外災變」。紫外災變是二十世紀之初物理學的又一朵烏雲，它的存在預示著能量均分定理並非永遠成立，而普朗克的能量量子化假設則為二十世紀物理學的另一大支柱——量子力學的建立開創了先河。

相對論

亨德里克·安東·勞侖茲

相對論產生的歷史背景

邁克生-莫雷實驗對以太風觀測的零結果表明，或許所有有關以太的理論需要修改，例如像勞侖茲那樣引入長度收縮因子，這樣會帶來一系列的修補工作；或者認為以太存在的理論根本就不成立。其實早在1865年馬克士威就已經證明電磁波傳播速度只和介質有關，1890年赫茲在研究電磁理論時也得出了電磁波波速與波源速度無關的結論。然而，這個結論顯然是不符合伽利略變換的，這說明對於運動中的物體需要一種新的電動力學。勞侖茲曾經在維持以太存在性的前提下發展過這樣一種電磁理論，這被稱作勞侖茲以太論。在這一理論中，以太和其他物質被嚴格區分開，以太是絕對靜止的，這也是牛頓的絕對時空觀的反映；然而有別於機械觀的以太，勞侖茲的以太是一種「電磁以太」：勞侖茲假設電磁場是以太狀態的體現，但他對此沒有做更多的解釋。勞侖茲用這一理論解釋了塞曼效應，為此獲得了1902年的諾貝爾物理學獎。1895年，勞侖茲給出了長度收縮的假設，並通過他的相關態定理提出了所謂「本地時」的概念，運用這一概念他解釋了光行差現象、都卜勒頻移和斐索流水實驗。相關態定理是說相對於以太運動的觀察者在他的參考系中觀測到的物理現象應當和靜止坐標系中的觀察者看到的是相同的。本地時的概念在數學上相當於狹義相對論中的相對同時概念，但在勞侖茲的理論中它只是一種數學上的輔助工具，沒有實在的物理意義。同一年，勞侖茲引入了一組適用於馬克士威電磁理論在相對以太運動的坐標系中時空變換的方程式，即勞侖茲變換，並於1899年和1904年對勞侖茲變換進行了補充和修正，他1904年的論文《以任意小於光速的系統中的電磁現象》給出的勞侖茲變換已經非常接近於現代的定義。

法國數學家、科學家昂利·龐加萊一直是勞侖茲觀點的闡釋者及批判者，1900年他對勞侖茲的本地時概念的起源作出了具有物理意義的解釋，即本地時來自不同坐標系間通過光速進行的時鐘同步，這就是狹義相對論中同時性的相對性的概念。1904年龐加萊在獨立於愛因斯坦工作的情形下提出了相對性原理：任何力學和電磁學實驗都不能區分靜止和等速運動的任何慣性參考系，這條原理後來成為狹義相對論的兩條基本原理之一。1905年6月5日，龐加萊在給勞侖茲的信中證明了勞侖茲於1904年論文中給出的電磁方程組不是勞侖茲協變的，並重新修正了勞侖茲變換的方程式。龐加萊的這一組方程式正是沿用至今的勞侖茲變換形式，也正是龐加萊此時首次將這一組方程式命名為勞侖茲變換。

勞侖茲建立的基本觀點是，在一組特定的變換下電磁場的方程組形式並不（隨坐標系）改變，我將這組變換稱做勞侖茲變換：

$x^{\prime }=k\ell \left(x+\varepsilon t\right)\!,\;t^{\prime }=k\ell \left(t+\varepsilon x\right)\!,\;y^{\prime }=\ell y,\;z^{\prime }=\ell z,\;k=1/{\sqrt {1-\varepsilon ^{2}}}.$
— 昂利·龐加萊， 論電子的動力學

他證明了勞侖茲變換是最小作用量原理的一個推論，並用群論的語言描述了勞侖茲變換，即勞侖茲群，這些內容都包含在他於1906年1月發表的論文《論電子的動力學》中。愛因斯坦將勞侖茲和龐加萊稱作相對論的先驅，他指出在他之前「勞侖茲已經認識到這種以他名字命名的變換對分析馬克士威方程組的重要作用，而龐加萊則做出了更深入的研究……」。

阿爾伯特·愛因斯坦

狹義相對論

主條目：狹義相對論發現史

論運動物體的電動力學

德國猶太物理學家阿爾伯特·愛因斯坦於1900年畢業於蘇黎世聯邦理工學院，而後於1901年獲瑞士國籍。愛因斯坦首先在各種對以太風觀測的零結果中猜想到以太的不存在性，並在對勞侖茲和龐加萊的理論的研究中發現了運動物體的電動力學導致的光速不變性與原本的速度疊加原理的矛盾。對於這一矛盾，愛因斯坦聲稱是其好友米歇爾·貝索幫助他領悟到了解決方案，即同時性的相對性。1905年6月30日，愛因斯坦完成了劃時代的著名論文：《論運動物體的電動力學》，並發表在同年9月的《物理年鑑》上。在這篇論文中，愛因斯坦開頭便指出了馬克士威電磁理論應用於運動物體時表現出的內在不對稱性（引用了一個著名的理想實驗——移動中的磁鐵與導體問題來說明），為同時性下了新的定義，從而引出了他的狹義相對論理論，這一理論基於兩個基本公設（原文用詞為「原理」）：

• 物理體系的狀態據以變化的定律，同描述這些狀態變化時所參照的坐標系究竟是兩個在互相勻速移動著的坐標系中的哪一個並無關係。
• 任何光線在「靜止」的坐標系中都是以確定的速度c運動著，不管這道光線是由靜止的還是運動的物體發射出來的。
  — 阿爾伯特·愛因斯坦， 論運動物體的電動力學

第一條公設也就相當於龐加萊的相對性原理，第二條公設來自於從馬克士威理論推出的光速不變原理。愛因斯坦首先從這兩條基本原理出發，從而可以推導出電動力學中坐標系的變換法則，即勞侖茲變換（這有別於勞侖茲首先從坐標變換規律出發的方法）。在勞侖茲變換的基礎上，愛因斯坦很自然地在論文的動力學部分中推導出長度收縮、時間膨脹、速度的合成等新的物理概念。在電動力學部分中，愛因斯坦描述了馬克士威-赫茲方程組在勞侖茲變換下的形式，並應用狹義相對論解釋了都卜勒頻移和光行差現象，以及加速電子的動力學。其中在有關加速電子的章節中，愛因斯坦得到了運動電子的相對論動能公式。同年11月，愛因斯坦在另一篇論文《物體的慣性同它所含的能量有關嗎？》中闡述了狹義相對論中的質能等價關係，從此提出有別於古典能量的「靜止能量」的概念。

狹義相對論的參考溯源

值得注意的是，《論運動物體的電動力學》沒有引用其他任何參考文獻，於是人們因此關注愛因斯坦在創立相對論時到底受到了哪些啟發。愛因斯坦本人聲稱他的思想受到了經驗主義哲學家大衛·休謨和恩斯特·馬赫的影響。其他影響愛因斯坦發展狹義相對論的物理研究應該還包括龐加萊的相對性原理、運動的磁體和導體問題、各種對以太風觀測實驗的否定結果——然而，愛因斯坦否認了其中最重要的實驗，即邁克生-莫雷實驗對他產生過任何重要影響。其他可能的參考來源還有龐加萊描述相對性原理的《科學與假說》，以及馬克斯·亞伯拉罕的著作，愛因斯坦從中借用了「馬克士威-赫茲方程組」和「縱向和橫向質量」等詞彙。根據他對於電動力學和光速不變原理的觀點，愛因斯坦認為勞侖茲在1895年的理論（所謂馬克士威-勞侖茲電動力學）和斐索流水實驗對他的思想產生過相當大的影響。1909年和1912年愛因斯坦兩次敘述說他曾借用過勞侖茲的靜止以太理論中的原理（意味著承認馬克士威方程組在以太系下的正確性以及光速不變），但他發現如果同時假設光速不變和相對性原理，則以太的概念是沒有用的。根據他1907年及其後續論文，這兩個原理看似矛盾之處是可以被解決的，方法就是不再將勞侖茲的本地時概念看作一個數學上的輔助參量，而是當作與信號速度有關的具有物理實在的時間。如前所述，龐加萊在獨立於愛因斯坦工作的情形下也得到了本地時的類似物理解釋，並且也和信號速度有關；然而他的不足之處在於仍然堅持認為在以太中的時間才是真正的時間，相對以太運動的時鐘指示的是表象的時間。愛因斯坦在1953年回憶狹義相對論的發展時曾說：「對我而言，我當時只了解勞侖茲於1895年的工作……而並不清楚他之後的工作，也不清楚龐加萊的後續研究。從這個意義上說，我在1905年的工作是獨立完成的……」。即使承認了勞侖茲、龐加萊和馬赫等人為狹義相對論的創立做出了重要鋪墊工作，但正如愛因斯坦所言，他在狹義相對論中無與倫比的突出貢獻是建立了馬克士威方程組和勞侖茲變換兩者之間的內在聯繫，並認識到在狹義相對論的框架下「勞侖茲不變性是任何物理定律都普遍具有的時空本性」。

早期科學界的接受

沃爾特·考夫曼

早期的物理學界對相對論一直持懷疑態度，即使到了1921年愛因斯坦獲諾貝爾獎的原因仍然並非由於相對論的建立。相對論最初的支持者大多來自愛因斯坦的故鄉德國：最早引用愛因斯坦工作的物理學家可能是德國實驗物理學家沃爾特·考夫曼，他在1905年至1906年間比較了勞侖茲和愛因斯坦的理論，並稱自己更偏好愛因斯坦的觀點，但他又認為這兩種理論在觀測上是等價的。從而他將相對性原理稱作「勞侖茲-愛因斯坦」的基本假設，而「勞侖茲-愛因斯坦理論」這一名稱也被其他人使用過數年之久。馬克斯·普朗克也隨後發表了他的第一篇有關相對論的論文，其中他將愛因斯坦的理論看作是勞侖茲理論的推廣。據研究表明，普朗克在1906年曾使用詞語「相對性理論」（Relativtheorie，這一名稱是相對亞伯拉罕的「球體理論」而言的）和「勞侖茲-愛因斯坦理論」並稱狹義相對論。愛因斯坦本人及其他一些人的稱法是「相對性原理」，很長一段時間裡這些不同的稱呼被不同的物理學家交替使用著。

1906年考夫曼發表了他對加速電子電荷質量比測量的實驗結果（即質量與速度的相關性），這一結果清楚地顯示了和相對性原理及勞侖茲-愛因斯坦理論的相違背，卻反而支持了亞伯拉罕理論。在這以後幾年裡，這一實驗都被看作是反對狹義相對論的有力佐證，而勞侖茲對這一實驗結果感到非常失望。然而德國物理學家阿爾弗雷德·布赫雷爾（1908年）等人的其後類似實驗都支持勞侖茲-愛因斯坦理論，反對亞伯拉罕的理論。不過，後來有人指出所有以上提到的實驗精度都不足以測量出勞侖茲-愛因斯坦理論和亞伯拉罕理論的區別，因此直到二十世紀四十年代更精確的實驗結果得出後才真正顯示出狹義相對論的正確性。

廣義相對論

相對性原理

愛因斯坦於1907年發表了論文《關於相對性原理和由此得出的結論》，這篇論文標誌著他對建立一個基於狹義相對論基礎的重力理論的漫長探索的開始。愛因斯坦試圖將牛頓萬有引力定律加以修改得能夠與狹義相對論互相融合．初步結果顯示這方向可行，然而，愛因斯坦並不滿意，因其中涉及到一些尚未建立的假說。有一天，他坐在他喜好的椅子上思考問題時，忽然靈機一動，「假若一個人自由地墜落，他必不會感覺到自己的重量。」他後來描述這是他一生最快樂的思維，其賦予他深刻的印象，激勵他繼續發展出合理的重力理論。愛因斯坦在這篇論文中將弱等效原理擴展為愛因斯坦等效原理：「在足夠小的時空區域中物理定律約化成狹義相對論中的形式；而且沒有任何局域實驗能夠探測到周圍重力場的存在。」既然非慣性系等價於重力場，愛因斯坦從而將狹義相對論中的相對性原理也做了推廣：在狹義相對論中所有的慣性系都是平權的，物理定律形式不變；但在新的理論中，所有的參考系都是平權的，物理定律形式不會因慣性系或非慣性系而改變，這一推廣的相對性原理被稱作廣義相對性原理。

重力場方程式的建立

馬塞爾·格羅斯曼

雖然認識到了狹義相對論需要推廣為廣義相對論，並確立了兩條基本原理，愛因斯坦仍然為探索這一新理論研究了八年之久（1907年至1915年）。這期間他面臨的一個主要問題是缺乏有效的數學工具，直到1913年他在德國數學家馬塞爾·格羅斯曼的幫助下發表了一篇突破性的論文：《廣義相對論和重力理論綱要》，題目標註了物理部分作者為愛因斯坦，數學部分作者為格羅斯曼。這篇論文中原來單一的牛頓純量重力場被一個具有十個分量的四階對稱黎曼張量重力場替代，從此物理學中的時空不再是平直的，而成為了在全局上具有曲率但在局部平直的黎曼流形。1914年，愛因斯坦發表了《廣義相對論正式基礎》，其中他得到了廣義相對論中描述粒子運動的方程式：測地線方程式，並籍此推導了重力場中的光線偏折和重力紅移的結果（此次得出的光線偏折結果並不正確，而愛因斯坦曾於1907年用等效方法推導出重力紅移）。1915年11月，愛因斯坦發表了他最終推導出重力場方程式的四篇論文，其中《用廣義相對論解釋水星近日點運動》證明了廣義相對論能夠解釋自1859年以來困擾天文學家的水星的反常進動現象，而《重力場方程式》則正式給出了描述重力場和物質交互作用的愛因斯坦重力場方程式。

亞瑟·斯坦利·愛丁頓爵士

廣義相對論的實驗驗證

廣義相對論創立之初還沒有一個穩固的實驗觀測基礎來證實，愛因斯坦本人提出過三種驗證廣義相對論的實驗方法，分別為水星軌道的近日點進動、太陽重力場中的光線偏折和光波的重力紅移。在當時只有第一種方法是很早就被觀測到的現象：1859年法國天文學家於爾班·勒威耶就發現水星的實際軌道進動與預期的並不十分相符，即使考慮到太陽系中其他行星的影響，實際的進動速度還是要比古典力學所預言的稍快一點（根據西蒙·紐康在1882年的計算，這個差值大約為每世紀43弧度秒）。在很長時間內這個原因都得不到合理的解釋，古典的假說包括行星際塵埃、太陽本身未被觀測到的橢球性、水星未被觀測到的衛星、水內小行星的存在，甚至有人猜測牛頓的萬有引力定律並非嚴格的平方反比律，但這些假說都沒能獲得成功。1915年，愛因斯坦在論文《用廣義相對論解釋水星近日點運動》中計算了水星在太陽重力場中的軌道進動並推導出了進動的角位移公式，所得的理論數值完全符合紐康的結果。

愛丁頓於1919年為驗證廣義相對論拍攝的日全食底片

1911年愛因斯坦在論文《論重力對光的傳播的影響》中提出光線在太陽附近經過時會因太陽重力場的作用導致傳播方向發生偏折，不過直到1915年他才給出正確計算得出的偏折角度。當時正值第一次世界大戰期間，英國與德國之間的學術交流也由此中斷。所幸的是，英國天體物理學家亞瑟·斯坦利·愛丁頓爵士當時在英國皇家天文學會任秘書一職，他通過來自荷蘭物理學家威廉·德西特的論文和書信成為了第一個了解廣義相對論的英國人。愛丁頓在當時是為數不多的具有良好數學功底從而能理解廣義相對論的天文學家，也因為他是當時為數不多的國際主義者和和平主義者，這都使得他有興趣去了解一名德國物理學家的理論。很快，愛丁頓成為了廣義相對論在英國的主要支持者和推廣者。戰後，愛丁頓於1919年5月29日前往西非幾內亞灣的普林西比島觀測日全食。日全食發生時他對太陽附近的恆星進行拍攝，由於光線在重力場中會發生偏折，拍攝到的恆星位置將會發生偏移。愛丁頓指出牛頓理論預言的偏移量將只有愛因斯坦理論所預言偏移量的一半，他的測量結果表明是支持愛因斯坦理論的。次年愛丁頓將這一結果發表並肯定了愛因斯坦的理論，這一發現隨後被全球報紙競相報導，一時間使愛因斯坦和廣義相對論名聲赫赫，有報道甚至撰文稱「發現了一個新宇宙」。

1925年美國威爾遜山天文台的沃爾特·亞當斯對天狼星的伴星天狼B譜線的觀測表明，譜線的頻移基本符合廣義相對論所預言的重力紅移值。1959年的龐德-雷布卡實驗利用梅斯堡效應測定的重力紅移值和理論值相差不超過5%。此後廣義相對論又產生了更多的實驗驗證方法，但那是二十世紀六十年代以後，天體物理學和宇宙學進入了所謂廣義相對論的黃金時代之後的事，這部分內容詳見下文當代天體物理學和宇宙學兩節。

量子理論

舊量子論

普朗克能量子

馬克斯·普朗克

1900年普朗克在黑體輻射研究中的能量量子化假說是量子理論建立的前奏。儘管在最初的思考中普朗克並不贊同波茲曼的統計理論，但由於他發現無法通過古典的熱力學定律來導出輻射定律，他不得不轉而嘗試統計規律，其結果就是普朗克黑體輻射定律。同時普朗克還計算得到了公式中的普適常數，即普朗克常數。然而即使如此，普朗克的能量量子化假說最初也未得到應有的重視，在當時的物理學界看來，將能量與頻率聯繫起來（即$\epsilon =h\nu \,$）是一件很不可理解的事，連普朗克本人對量子化也深感懷疑，他仍然試圖尋找用古典手段解決問題的辦法。

1905年，愛因斯坦在他的革命性論文《關於光的產生和轉變的一個啟發試探性的觀點》中秉承了普朗克的能量量子化假說，提出了光量子的概念。在愛因斯坦看來，將光看作是一份份不連續的能量子將有助於理解一些電磁理論無法理解的現象：

在我看來，如果假定光的能量在空間的分布是不連續的，就可以更好地理解黑體輻射、光致發光、紫外線產生陰極射線，以及其他有關光的產生和轉變的現象的各種觀測結果……這些能量子在運動中不再分散，只能整個地被吸收或產生。
— 阿爾伯特·愛因斯坦， 關於光的產生和轉變的一個啟發性的觀點

如前所述，這裡提到的陰極射線正是光電效應所產生的電流。愛因斯坦進一步將光量子概念應用到光電效應的解釋中，並提出了描述入射光量子能量與逸出電子能量之間關係的愛因斯坦光電方程式。雖然這一理論在1905年就已提出，真正通過實驗驗證則是美國物理學家羅伯特·密立坎在1916年才完成的。密立坎的光電效應實驗測量了愛因斯坦所預言的遏制電壓和頻率的關係，其曲線斜率正是普朗克在1900年計算得到的普朗克常數，從而「第一次判決性地證明了」愛因斯坦光量子理論的正確。不過，密立坎最初的實驗動機恰恰相反，其本人和當時大多數人一樣，對量子理論持相當大的保守態度。

1906年，愛因斯坦將普朗克定律應用於固體中的原子振動模型，他假設所有原子都以同一頻率振動，並且每個原子有三個自由度，從而可求和得到所有原子振動的內能。將這個總能量對溫度求導數就可得到固體熱容的表達式，這一固體熱容模型從而被稱作愛因斯坦模型。這些內容發表於1907年的論文《普朗克的輻射理論和比熱容理論》中。

波耳模型

尼爾斯·波耳

1903年，長岡半太郎最早發展出原子的準行星模型，稱為半太郎土星模型。他認為，原子是由一個位於中心帶正電的大圓球與上百個環繞在四周帶負電的電子所組成，這些電子被靜電力穩定束縛於原子內部，就如同由很多小顆粒物質組成的土星環因重力而穩定環繞於土星四周。半太郎聲稱，原子光譜應該直接與電子的軌道頻率有關，而原子的放射性行為是因為偶而發生的土星環崩潰導致電子從原子裡被射出。然而，半太郎模型的種種理論預測不符合實驗結果。另外，辦太郎模型的電子軌道，對於垂直於轉動平面的震盪，無法維持穩定性。這穩定性問題最終促使長岡半太郎在1908年放棄這模型。

1908年至1909年間，歐尼斯特·拉塞福在研究α粒子散射的過程中發現了α粒子的大角度散射現象，從而猜想原子內部存在一個強電場。其後他於1911年發表了論文《物質對α、β粒子的散射和原子構造》，通過散射實驗的結果提出了全新的原子結構模型，稱為拉塞福模型：正電荷集中在原子中心，即原子中心存在原子核，在原子核的四周是帶負電的電子雲。從拉塞福模型，拉塞福推導出散射公式，其預測與實驗結果相符合。然而，在拉塞福散射實驗裡，主角是原子核，而電子並不重要，因此拉塞福不能無憑無據地給出原子的電子組態，也無法用這模型對於化學結合、元素列表、原子光譜給出解釋。儘管拉塞福模型並不完備，它為後來的波耳模型奠定了良好的基礎。

1912年至1913年間，丹麥物理學家尼爾斯·波耳指出，原子的穩定性問題不能在古典電動力學的框架下解決，而唯有依靠量子化的方法。波耳從氫原子光譜的巴耳末公式和約翰尼斯·史塔克的價電子躍遷輻射等概念受到啟發，對圍繞原子核運動的電子軌道進行了量子化，而原子核和電子之間的動力學則依然遵守古典力學，因此一般來說波耳模型是一種半古典理論。這些內容發表在他1913年的著名三部曲論文《論原子構造和分子構造》中。論文中他建立了一個電子軌道量子化的氫原子模型，這一模型是基於兩條假設之上的：

• 體系在定態中的動力學平衡可以藉普通力學進行討論，而體系在不同定態之間的過渡則不能在這基礎上處理。
• 後一過程伴隨有均勻輻射的發射，其頻率與能量之間的關係由普朗克理論給出。

— 尼爾斯·波耳， 論原子構造和分子構造

阿諾·索末菲

這一模型良好地描述了氫原子光譜的規律，並且和實驗觀測值相當符合。此外，波耳還從對應原理出發，將電子軌道角動量也進行了量子化，並給出了電子能量、角頻率和軌道半徑的量子化公式。波耳模型在解釋氫原子的發射和吸收光譜中取得了重大成功，是量子理論發展的重要里程碑。

不過，波耳模型只能解釋氫原子光譜，對其他稍複雜的原子光譜就毫無辦法，它創立之時人們還沒有自旋的概念，從而波耳模型無法解釋原子譜線的塞曼效應和精細結構；波耳模型也無法說明電子在兩條軌道之間躍遷的過程中到底是處於一種什麼狀態。包立批評這為「糟糕的躍遷」。

德國物理學家阿諾·索末菲在1914年至1915年間發展了波耳理論，他提出了電子橢圓軌道的量子化條件，從而將克卜勒運動納入到量子化的波耳理論中並提出了空間量子化概念，他還給量子化公式添加了狹義相對論的修正項。索末菲的量子化模型很好地解釋了正常塞曼效應、史塔克效應和原子譜線的精細結構，他的理論收錄在他在1919年出版的《原子結構與光譜線》一書中。索末菲在波耳模型的基礎上給出了更一般化的量子化條件：$\oint p_{i}dq_{i}=n_{i}h\,\!$，這一條件被稱作舊量子條件或威耳遜-索末菲量子化定則，與之相關聯的理論是埃倫費斯特指出的被量子化的物理量是一個絕熱不變量。

波粒二象性

路易·德布羅意

1905年愛因斯坦對電磁輻射的能量進行量子化從而提出了光量子的概念，但此時的光量子只是能量不連續性的一種體現，還不具有真實的粒子概念。1909年，愛因斯坦發表了《論我們關於輻射的本性和組成的觀點的發展》，在這篇發言兼論文中愛因斯坦證明了如果普朗克黑體輻射定律成立，則光子必須攜帶有動量並應被當作粒子對待，同時還指出電磁輻射必須同時具有波動性和粒子性兩種自然屬性，這被稱作波粒二象性。1917年，愛因斯坦在《論輻射的量子理論》中更深入地討論了輻射的量子特性，他指出輻射具有兩種基本方式：自發輻射和受激輻射，並建立了一整套描述原子輻射和電磁波吸收過程的量子理論，這不但成為五十年後雷射技術的理論基礎，還促成了現代物理學中迄今最精確的理論——量子電動力學的誕生。1923年，美國物理學家阿瑟·康普頓在研究X射線被自由電子散射的情況中發現X射線出現能量降低而波長變長的現象，他用愛因斯坦的光量子論解釋了這一現象並於同年發表了《X射線受輕元素散射的量子理論》。康普頓效應從而成為了光子存在的論斷性證明，它證明了光子攜帶有動量，愛因斯坦在1924年的短評《康普頓實驗》中高度評價了康普頓的工作。

1923年，法國物理學家路易·德布羅意在光的波粒二象性，以及布里元為解釋波耳氫原子定態軌道所提出的電子駐波假說的啟發下，開始了對電子波動性的探索。他提出了實物粒子同樣也具有波粒二象性的假說，對電子而言，電子軌道的周長應當是電子對應的所謂「位相波」波長的整數倍。德布羅意在他的博士論文中闡述了這一理論，但他同時認為他的電子波動性理論所描述的波的概念「像光量子的概念一樣，只是一種解釋」，因此真正的粒子的波函數的概念是等到薛丁格建立波動力學之後才完備的。另外，德布羅意在論文中也並沒有明確給出物質波的波長公式$\lambda =h/p\,$，雖然這一想法已經反映在他的內容中。德布羅意的博士論文被愛因斯坦看到後得到了很大的讚許，愛因斯坦並向物理學界廣泛介紹了德布羅意的工作。這項工作被認為是統一了物質粒子和光的理論，揭開了波動力學的序幕。1927年，貝爾實驗室的柯林頓·戴維孫和雷斯特·革末進行了著名的戴維孫-革末實驗，他們將低速電子射入鎳晶體，觀測每一個角度上被散射的電子強度，所得的繞射圖案與布拉格預測的X射線的繞射圖案相同，這是電子也會像波一樣發生繞射的確鑿證明。特別地，他們發現對於具有特定能量的入無線電子，在對應的散射角度上散射最明顯，而從布拉格光柵繞射公式得到的繞射波長恰巧等於實驗中具有對應能量電子的德布羅意波長。

現代量子力學

矩陣力學

維爾納·海森堡

有別於舊量子論的現代量子力學的誕生，是以1925年德國物理學家維爾納·海森堡建立矩陣力學和奧地利物理學家埃爾溫·薛丁格建立波動力學和非相對論性的薛丁格方程式，從而推廣了德布羅意的物質波理論為標誌的。矩陣力學是第一個完備且被正確定義的量子力學理論，通過將粒子的物理量闡釋為隨時間演化的矩陣，它能夠解釋波耳模型所無法理解的躍遷等問題。矩陣力學的創始人是海森堡，另外他的德國同胞馬克斯·玻恩和帕斯庫爾·約當也做出了重要工作。

1924年，23歲的海森堡還只是哥廷根大學未取得終身教職的一名年輕教師，他於同年九月應波耳的邀請來到哥本哈根進行六個月的交流訪問，此間海森堡受到了波耳和他的學生漢斯·克喇末等人的深刻影響。1925年海森堡回到哥廷根，在五月之前他的工作一直是致力於計算氫原子譜線並試圖只採用可觀察量來描述原子系統。同年六月為了躲避鼻炎的流行，海森堡前往位於北海東部並且沒有花粉侵擾的黑爾戈蘭島。在那裡他一邊品味歌德的抒情詩集，一邊思考著光譜的問題，並最終意識到引入不可對易的可觀察量或許可以解決這個問題。其後他在回憶中寫道：「當時正是凌晨三點，最終的計算結果即將出現在我面前，起初這讓我深深震撼了。我非常興奮以至於無法考慮睡覺的事，於是我離開房間前往岩石的頂端等待朝陽。」回到哥廷根後，海森堡將他的計算遞交給沃夫岡·包立和馬克斯·玻恩評判，他對包立附加評論說：「所有內容對我來說都還很不清楚，但似乎電子不應當在軌道上運動了」。在海森堡的理論中，電子不再具有明確的軌道，他從而意識到電子的躍遷機率並不是一個古典量，因為在描述躍遷的傅立葉級數中只有頻率是可觀察量。他用一個係數矩陣取代了古典的傅立葉級數，在古典理論中傅立葉係數表徵著輻射的強度，而在矩陣力學中表徵強度的則是位置算符的矩陣元的大小。海森堡理論的數學形式中系統的哈密頓量是位置和動量的函數，但它們不再具有古典力學中的定義，而是由一組二階（代表著過程的初態和終態）傅立葉係數的矩陣給出。玻恩在閱讀海森堡的理論時，發現這一數學形式可以用系統化的矩陣方法來描述，這一理論從而被稱作矩陣力學。於是玻恩和他的助手約爾當一起發展了這種理論的嚴謹數學形式，他們的論文在海森堡的論文發表六十天後也公布於眾。同年11月16日，玻恩、海森堡和約爾當三人又聯合發表了一篇後續論文，論文將情形推廣到多自由度及含有簡併、定態微擾和含時微擾，全面闡述了矩陣力學的基本原理：

1. 所有的可觀察量都可用一個厄米矩陣表示，一個系統的哈密頓量是廣義坐標矩陣和與之共軛的廣義動量矩陣的函數。
2. 可觀察量的觀測值是厄米矩陣的本徵值，系統能量是哈密頓量的本徵值。
3. 廣義坐標和廣義動量滿足正則對易關係（強量子條件）。
4. 躍遷頻率滿足頻率條件。

如上所述，海森堡的矩陣力學所基於的觀念是，電子本身的運動是無法觀測的，例如在躍遷中只有頻率是可觀察量，只有可觀察量才可被引入物理理論中。因此如果不能設計一個實驗來準確觀測電子的位置或動量，則談論一個電子運動的位置或動量是沒有意義的。1927年，海森堡從位置和動量的共軛對易關係推導出了兩者的不確定性之間的關係，這被稱作不確定性原理。海森堡設想了一個理想實驗，即著名的海森堡顯微鏡實驗，來說明電子位置和動量的不確定性關係；以及通過斯特恩-蓋拉赫實驗來說明自旋的幾個正交分量彼此之間的不確定性關係。不過，波耳雖然對海森堡的不確定性原理表示贊同，卻否定了他的理想實驗。波耳認為不確定性原理其實是波粒二象性的體現，但實驗觀測中只能展示出粒子性或波動性兩者之一，即不可能同時觀測到電子的粒子性和波動性，這被波耳稱作互補原理。海森堡的不確定性原理、波耳的互補原理和波恩的波函數統計詮釋以及相關聯的量子觀念，構成了被當今物理學界最為認可的量子力學思想——哥本哈根詮釋。

波動力學

埃爾溫·薛丁格

1925年，在蘇黎世大學擔任教授的埃爾溫·薛丁格讀到了德布羅意有關物質波理論的博士論文，薛丁格本人又受愛因斯坦波粒二象性等思想的影響頗深，他從而決定建立一個描述電子波動行為的波方程式。當時由於人們還不十分理解電子自旋這一量子力學中最大的相對論效應，薛丁格還無法將波動方程式納入狹義相對論的框架中，他從而試圖建立了一個非相對論性的波方程式。1926年1月至6月間，薛丁格發表了四篇都名為《量子化就是本徵值問題》的論文，詳細論述了非相對論性電子的波動方程式、電子的波函數以及相應的本徵值（量子數）。哈密頓曾認為力學是波動理論在波長為零時的極限情形，而薛丁格正是受此引導發展了這一觀念，他將哈密頓力學中的哈密頓-雅可比方程式應用於愛因斯坦的光量子理論和德布羅意的物質波理論，利用變分法得到了非相對論量子力學的基本方程式——薛丁格方程式。

薛丁格發現這個定態方程式的能量本徵值正對應著氫原子的能階公式，由此他得出，量子化條件是不需要像波耳和索末菲那樣人為引入的，它可以很自然地從本徵值問題推出。在三維球坐標系下將薛丁格方程式應用於氫原子可以得到三個量子化條件：軌道量子數（決定電子的能階）、角量子數（決定電子的軌道角動量）和磁量子數（決定電子在垂直方向的磁矩）。在其後的論文中，他分別討論了含時的薛丁格方程式、諧振子、微擾理論，並應用這些理論解釋了史塔克效應和色散等問題。薛丁格把自己的理論稱作波動力學，這成為了現代量子力學的另一種形式。特別是，薛丁格的理論是以一個偏微分方程式為基礎的，這種波動方程式對人們而言相當熟悉，相比之下海森堡的矩陣力學所採用的數學形式則不那麼易懂（在海森堡的理論之前，矩陣只是數學家的玩具，從未被引入任何物理理論中）。因此一開始波動力學比矩陣力學要更受科學界的青睞，愛因斯坦、埃倫費斯特等人對薛丁格的工作都非常讚賞。直到1926年薛丁格在研究海森堡的理論之後，發表了《論海森堡、玻恩與約爾當和我的量子力學之間的關係》，證明了兩種理論的等價性；不過，對當時大多數的物理學家而言，波動力學中數學的簡明性仍然是顯而易見的。

波動力學建立後，人們還一直不清楚波函數的物理意義，薛丁格本人也只能認為波函數代表著粒子波動性的振幅，而粒子則是多個波函數所構成的波包（所謂電子云模型）。1926年，玻恩在愛因斯坦光量子理論中光波振幅正比於光量子的機率密度這一觀點的啟發下，聯繫到量子力學中的散射理論，提出了波函數的統計詮釋：波函數是一種機率波，它的振幅的平方正比於粒子出現的機率密度，並且波函數在全空間的積分是歸一的。玻恩由於波函數的統計詮釋獲得了1954年的諾貝爾物理學獎。

相對論量子力學

保羅·狄拉克

1921年，德國物理學家阿爾弗雷德·朗德指出反常塞曼效應意味著電子的磁量子數只能為半整數。1924年，奧地利物理學家沃夫岡·包立提出這個半整數代表著電子的第四個自由度，並在此基礎上提出了包立不相容原理。包立最初未能對這第四個自由度的物理意義作出解釋，但其後美國物理學家拉爾夫·克羅尼格提出這個自由度可以看作是電子的一種內稟角動量，相當於電子在沿自己的軸旋轉，然而包立對此不以為然，他很反對將這種古典力學模型引入量子力學中。不過僅半年後，埃倫費斯特的兩個學生：烏倫貝克和古茲米特再次提出了類似的自旋假說，兩人在埃倫費斯特的推薦下投稿給《自然》雜誌。儘管勞侖茲從這種假說得出電子表面速度將遠遠大於光速，但其後由於波耳、海森堡和英國物理學家盧埃林·托馬斯等人在相對論力學下的計算都支持這一理論，海森堡和約爾當用矩陣對自旋做了充分的描述，自旋模型最終得到了充分肯定。不過，包立始終反對這種「電子自轉」的古典模型，而他最終也真正做到了將電子自旋和自轉嚴格區別：自旋並不是電子做的古典的自轉，它應當理解為電子的一種內稟屬性，這種屬性被包立用量子化的矩陣來描述。包立後來將自旋的概念引入薛丁格方程式中，得到了在外加電磁場作用下考慮電子自旋的量子力學波動方程式，即包立方程式。

沃夫岡·包立

1928年，英國物理學家保羅·狄拉克在包立方程式的基礎上，試圖建立一個滿足勞侖茲協變性並能夠描述自旋為1/2粒子的薛丁格方程式，這麼做的部分動機也是試圖解決描述自旋為零的相對論性波方程式——克萊因-戈爾登方程式所出現的負值機率密度和負能量的問題。狄拉克考慮到薛丁格方程式只含對時間的一階導數而不具有勞侖茲協變性，他從而引入了一組對空間的一階導數的線性疊加，這組疊加的係數是滿足勞侖茲協變性的矩陣。由於係數是矩陣，則原有的波函數必須改為向量函數，狄拉克將這些向量函數稱作旋量。如此得到的波動方程式被稱作狄拉克方程式，它成為了相對論量子力學的基本方程式，同時它在量子場論中也是描述自旋為1/2粒子（夸克和輕子）的基本旋量場方程式。在此項工作中狄拉克首創了「量子電動力學」一詞，他從而被看作是量子電動力學的創始人。狄拉克發現，雖然旋量的機率密度可以保證為正值，方程式的本徵值卻仍然會出現負能量。在理論上如果電子可以擁有能階低至靜止能量負值的負能量態，則所有的電子都能通過輻射光子而躍遷到這一能階，狄拉克由此推算出在這種情形下整個宇宙會在一百億分之一秒內毀滅。狄拉克對這一問題的解釋是著名的狄拉克之海：真空中排滿了具有負能量的電子，在包立不相容原理的制約下正能量的電子無法躍遷到負能量態。同時，狄拉克還由此提出了反電子的存在，它同時具有負能量態電子的所有相反屬性，即具有正能量和正電荷。1932年狄拉克關於反物質存在的預言通過美國物理學家卡爾·安德森使用宇宙射線製造出正電子的實驗得到了證實。

1930年，狄拉克出版了他的量子力學著作《量子力學原理》，這是整個科學史上的一部里程碑之作，至今仍然是流行的量子力學教材之一。狄拉克在這部著作中將海森堡的矩陣力學和薛丁格的波動力學統一成同一種數學表達：

1. 用相空間中的厄米算符來表示可觀察量，並用希爾伯特空間中的向量來表示系統的量子態。
2. 對可觀察量而言，厄米算符的本徵態構成一個正交歸一的完備坐標系，所有可觀察量的測量值都是厄米算符的本徵值，對系統的測量會導致系統的波函數塌縮到對應的本徵態。
3. 共軛算符之間滿足正則對易關係，從而可得到不確定性原理。
4. 量子態隨時間的動力學演化可由含時的薛丁格方程式描述（薛丁格繪景），算符隨時間的動力學演化可由類似的海森堡方程式描述（海森堡繪景），這兩者是等價的。

1939年狄拉克引入了他的數學符號系統——狄拉克符號，並應用到《量子力學原理》中。直到今天，狄拉克符號仍然是最廣泛使用的一套量子力學符號系統。

波耳-愛因斯坦論戰

波耳和愛因斯坦在埃倫費斯特的家中（1925年）

量子力學的確令人印象深刻，但內心中有個聲音告訴我這不符合實際情況。這個理論解釋了很多，但沒有真正讓我們離那個「老傢伙」的秘密更近一步。我，無論如何都有理由相信，他不擲骰子。
— 愛因斯坦於1926年12月4日寫給玻恩的信

波耳、海森堡等人建立哥本哈根詮釋之後，立刻遭到了以愛因斯坦為首的一批物理學家的反對。愛因斯坦非常反對哥本哈根學派所作出的波函數的詮釋、不確定性原理以及互補原理等觀點。在愛因斯坦看來，電子的這種「自由意志」行為是違反他所鍾愛的因果律的，他從而認為波函數只能反映一個系綜的粒子的量子行為，而不像是波耳所說的一個粒子的行為。這種矛盾引發了分別以波耳和愛因斯坦為代表的兩種學說的論戰，時間長達半個多世紀之久。

1927年第五次索爾維會議

1927年的第五次索爾維會議上雙方爆發了公開的論戰。德布羅意在會中發表了他原創的導航波理論，其可以對於波函數的統計詮釋給出另一種替代詮釋，然而這理論遭到波耳與薛丁格等人大肆抨擊。德布羅意因此期望愛因斯坦給予支持，但是愛因斯坦選擇保持沉默。其後玻恩和海森堡發表了他們關於矩陣力學與的觀點，並在最後陳述說：「我們主張，量子力學是一種完備的理論，它的基本物理假說和數學假設是不能進一步被修改的。」愛因斯坦除了對於統計詮釋發表一些簡單的反對意見以外，並沒有在會議中發表甚麼意見，但在住宿旅館的餐廳裡，他與波耳等人進行了多次激盪的研討，愛因斯坦提出一個理想實驗：愛因斯坦狹縫，用來質疑位置-動量不確定性原理的正確性。後來波耳和海森堡等人對愛因斯坦的理想實驗做了批判，但愛因斯坦並沒有因此改變自己的觀點。於是在三年後的第六次索爾維會議上，愛因斯坦再次提出了另一個理想實驗：愛因斯坦光盒，用來說明時間-能量不確定性原理的不正確。這一理想實驗起初讓波耳非常困擾，但經過一天的思索，他發現愛因斯坦忽略了測量時的廣義相對論效應導致的時間不確定性，從而不確定性原理仍然成立。

兩次挑戰不確定性原理的失敗嘗試，迫使愛因斯坦認識到量子力學理論本身是自洽的，他從而轉向討論量子力學的完備性。1935年愛因斯坦和美國物理學家鮑里斯·波多爾斯基、納森·羅森聯合發表了論文《能認為量子力學對物理實在的描述是完備的嗎？》，提出量子力學對物理實在的描述是不完備的。為了說明這一點，他們提出了一個著名的理想實驗：愛因斯坦-波多爾斯基-羅森悖論（也稱作EPR悖論）並從這個實驗得到結論：或者，在量子力學中波函數對物理實在的描述是不完備的；或者，兩個對應於不可對易算符的物理量不能同時是實在的。而後他們通過分析指出，如果否定第一點則也必須否定第二點，從而波函數對物理實在的描述是不完備的。不過在波耳看來，從實證主義的意義上說這種悖論根本不成立，因為哥本哈根學派認為只有可觀測才意味著物理實在。儘管如此，愛因斯坦和波耳兩個人終生都沒有被對方說服。同年，愛因斯坦和薛丁格就EPR悖論在書信中交換了意見。薛丁格為了進一步顯示量子力學的不完備性，將量子力學應用到宏觀效應中，從而構思了著名的薛丁格貓思想實驗。1953年，英國物理學家大衛·玻姆同樣認為哥本哈根詮釋對物理實在的解釋是不完備的，需要附加的參量來描述，他從而提出隱變量理論；1965年，北愛爾蘭物理學家約翰·貝爾在此基礎上提出貝爾不等式，這為隱變量理論提供了實驗驗證方法。從二十世紀七十年代至今，對貝爾不等式的驗證給出的大多數結果是否定的；即使如此，波耳-愛因斯坦論戰的結果至今還未有最終的定論。

量子場論

量子電動力學

理察·費曼

量子電動力學起源於1927年保羅·狄拉克將量子理論應用於電磁場量子化的研究工作。他將電荷和電磁場的交互作用處理為引起能階躍遷的微擾，能階躍遷造成了發射光子數量的變化，但總體上系統滿足能量和動量守恆。狄拉克成功地從第一性原理導出了愛因斯坦係數的形式，並證明了光子的玻色-愛因斯坦統計是電磁場量子化的自然結果。現在人們發現，能夠精確描述這類過程是量子電動力學最重要的應用之一。另一方面，狄拉克所發展的相對論量子力學是量子電動力學的前奏，狄拉克方程式作為狹義相對論框架下量子力學的基本方程式，所描述的電子等費米子的旋量場的正則量子化是由匈牙利-美國物理學家尤金·維格納和約爾當完成的。狄拉克方程式所預言的粒子的產生和湮沒過程能用正則量子化的語言重新加以描述。

經歷了早期取得的成功之後，量子電動力學遭遇了理論上一系列嚴重的困難：很多原本看上去平常的物理量，例如在外界電場作用下電子的能態變化（在量子電動力學的觀點看來屬於電子和光子的交互作用），在量子場論的計算方法下會發散為無窮大。到了二十世紀四十年代，這一問題被美國物理學家理察·費曼、朱利安·施溫格、日本物理學家朝永振一郎等人突破性地解決了，他們所用的方法被稱為重整化。儘管他們各自研究所用的數學方法不同，美籍英裔物理學家弗里曼·戴森於1949年證明了費曼所用的路徑積分方法和施溫格與朝永振一郎所用的算符方法的等價性。量子電動力學的研究在這時達到了頂峰，費曼所創造的費曼圖成為了研究交互作用場的微擾理論的基本工具，從費曼圖可直接導出粒子散射的S矩陣。費曼圖中的內部連線對應著交互作用中交換的虛粒子的傳播子，連線相交的頂點對應著拉格朗日量中的交互作用項，入射和出射的線則對應初態和末態粒子的能量、動量和自旋。由此，量子電動力學成為了第一個能夠令人滿意地描述電子與反電子（旋量場）和光子（規範場）以及粒子產生和湮沒的量子理論。

量子電動力學是迄今為止建立的最精確的物理理論：量子電動力學的實驗驗證的主要方法是對精細結構常數的測量，至今在不同的測量方法中最精確的是測量電子的反常磁矩。量子電動力學中建立了電子的無因次旋磁比（即朗德g因子）和精細結構常數的關係，磁場中電子的迴旋頻率和它的自旋進動頻率的差值正比於朗德g因子。從而將電子迴旋軌道的量子化能量（朗道能階）的極高精度測量值和電子兩種可能的自旋方向的量子化能量相比較，就可從中測得電子自旋g因子，這項工作是由哈佛大學的物理學家於2006年完成的，實驗測得的g因子和理論值相比誤差僅為一萬億分之一，而進一步得到的精細結構常數和理論值的誤差僅為十億分之一。對芮得柏常量的測量到目前為止是精度僅次於測量反常磁矩的方法，但它的精確度仍要低一個數量級以上。

量子色動力學

戴維·格婁斯

二十世紀五十年代氣泡室和火花室的發明，使實驗高能物理學家發現了一批種類數量龐大並仍在不斷增長的粒子——強子，種類如此繁多的一批粒子應當不會是基本粒子。維格納和海森堡起初按電荷和同位旋對這些強子進行了分類，1953年美國物理學家默里·蓋爾曼和日本物理學家西島和彥在分類時又考慮了奇異數。1961年，蓋爾曼和以色列物理學家尤瓦爾·奈曼）進一步提出了強子分類的八重態模型。蓋爾曼和蘇聯物理學家喬治·茨威格於1963年修正了由日本物理學家坂田昌一早先提出的理論，並提出強子的分類情形可以用強子內部存在的具有三種味的更基本粒子——夸克來解釋。

蘇聯物理學家尼古拉·博戈柳博夫和他的學生在1965年提出，對於由三個反對稱的（即具有同向自旋）奇夸克組成的Ω重子，由於這種情形違反包立不相容原理，夸克應當具有一個另外的量子數。同樣的情形也出現在Δ⁺⁺重子中，在夸克模型中它由三個反對稱的上夸克組成。同年，日本物理學家南部陽一郎等人分別獨立提出夸克應當具有一個額外的SU(3)規範對稱的自由度，這種自由度後來被稱作色荷。南部等人還進一步提出了傳遞夸克之間交互作用的媒介子模型，這種媒介子是一組八種色的規範玻色子：膠子。

實驗中對自由夸克的檢測總是以失敗告終，這使得蓋爾曼一再聲稱夸克只是存在於數學上的結構，不代表真實的粒子；不過他的意思實際是指夸克是被禁閉的。費曼認為高能實驗已經證明了夸克是物理實在的粒子，並按他的習慣稱之為部分子。蓋爾曼和費曼的不同觀點在理論物理學界產生了深刻的分歧，費曼堅持認為夸克和其他粒子一樣具有位置和動量的分布，蓋爾曼則認為雖然特定的夸克電荷是可以定域化的，但夸克本身則有可能是無法定域化的。美國物理學家詹姆斯·比約肯指出如果夸克真的像部分子那樣是實在的點粒子，則電子和質子的深度非彈性散射將滿足特定關係，這一實驗由史丹佛直線加速器中心於1968年證實。1973年，美國物理學家戴維·格婁斯和他的學生弗朗克·韋爾切克，以及美國物理學家休·波利策發現了強交互作用中的漸近自由性質，這使得物理學家能夠利用量子場論中的微擾方法對很多高能實驗作出相當精確的預言。1979年，德國電子加速器中心的正電子-電子串聯環形加速器（PETRA）發現了膠子存在的直接證據。

與高能下的漸進自由相對的是低能下的色禁閉：由於色荷之間的作用力不隨距離增大而減小，現在普遍認為夸克和膠子永遠無法從強子中釋放。這一理論已經在格點量子色動力學的計算中被證實，但沒有數學上的嚴格分析。克雷數學研究所懸賞一百萬美元的「千禧年大獎難題」之一正是嚴格證明色禁閉的存在。

原子核物理和粒子物理

原子核物理學

歐尼斯特·拉塞福

歐尼斯特·拉塞福在1911年在拉塞福模型裡提議，在原子的中心存在著原子核，之後，他的學生漢斯·蓋革和歐尼斯特·馬斯登做實驗證實這劃時代理論，從此開啟了一門新的物理學分支——原子核物理學。在這之前的幾個代表性發現包括：1896年法國物理學家亨利·貝可勒爾發現天然放射性；居禮夫婦於1898年發現放射性元素釙、1902年發現放射性元素鐳；1899年，從鈾的放射線中，拉塞福發現了α射線和β射線隔年，法國物理學家保羅·維拉爾發現γ射線，而拉塞福和貝可勒爾等人又通過多個實驗進一步判斷了這幾種射線的本質。1919年，拉塞福使用α粒子（氦核）轟擊氮原子，將氮原子的一個質子擊走，首次通過人工核轉換製成氧-17。

二十世紀二十年代，量子力學的建立給原子核物理帶來了嶄新的面貌。1932年密立坎的學生卡爾·安德森在不了解狄拉克理論的情況下通過觀測雲室中的宇宙射線發現了正電子。同年，查兌克在拉塞福提出的原子核內具有中子的假說的基礎上，在卡文迪許實驗室進行了一系列粒子撞擊實驗，並計算了相應粒子的能量。查兌克的實驗證實了原子核內中子的存在，並測定了中子的質量。中子的發現改變了原子核原有的質子-電子模型，維爾納·海森堡提出新的質子-中子模型，在這模型裡，除了氫原子核以外，所有原子核都是由質子與中子組成。1934年，法國的約里奧-居禮夫婦通過用放射性釙所產生的α射線轟擊硼、鎂、鋁等輕元素，會發射出很多粒子產物，儘管之後移開放射性釙，仍舊會繼續發射粒子產物，這個現象導致了他們發現了人工放射性。1934年，義大利物理學家恩里科·費米在用中子轟擊當時已知的最重元素——92號元素鈾時，得到了一種半衰期為13分鐘的放射性元素，但它不屬於任何一種已知的重元素。費米等人懷疑它是一種未知的原子序數為93的超鈾元素，但在當時的條件下他無法做出判斷。同年，費米又通過用中子和氫核碰撞獲得了慢中子，慢中子的產生大大加強了中子在原子核實驗中的轟擊效果。

1946年，在比基尼環礁進行的十字路口行動核試驗

1938年德國化學家奧托·哈恩和弗里茨·施特拉斯曼用慢中子轟擊鈾，從中得到了較輕的元素：鑭和鋇。哈恩將這一結果發信給當時受納粹迫害而流亡中的好友，奧利地-瑞典物理學家莉澤·邁特納，稱自己發現了一種「破裂」的現象。邁特納次年在波耳的肯定下發表了論文《中子導致的鈾的裂體：一種新的核反應》，將這種現象稱作核分裂，並為裂變提供了理論上的解釋。邁特納所用的解釋就是愛因斯坦的狹義相對論中的質能等價關係，從而解釋了裂變中產生的巨大能量的來源。她計算出每個裂變的原子核會釋放2億電子伏特的能量，這一理論解釋奠定了應用原子能的基礎。同年，德國-美國物理學家漢斯·貝特解釋了恆星內部的核融合循環。

粒子物理學

介子的發現

湯川秀樹

粒子物理學是原子物理和原子核物理在高能領域的一個重要分支，相對於偏重於實驗觀測的原子核物理學，粒子物理更注重對基本粒子的物理本性的研究。就實驗方面而言，研究粒子物理所需的能量往往要比原子核物理所需的高得多，在迴旋加速器發明以前，很多新粒子都是在宇宙射線中發現的，如正電子。1935年，日本物理學家湯川秀樹提出了第一個重要的核子間強交互作用的理論，從而解釋了原子核內的質子和中子如何束縛在一起的。在湯川的理論中，核子間的作用力是靠一種虛粒子——介子來完成的。介子所傳遞的強交互作用能夠解釋原子核為何不在質子間相對較弱的電磁斥力下崩塌，而介子本身具有的兩百多倍電子靜止質量也能解釋為什麼強交互作用相比於電磁交互作用具有短很多的作用範圍。1937年，安德森等人在宇宙射線中發現了質量約為電子靜止質量207倍的新粒子——緲子，人們起初以為緲子正是湯川預言的介子，從而稱之為μ介子。然而隨著研究發現，緲子和原子核的交互作用非常微弱，事實證明它只是一種輕子。1947年，英國布里斯托大學的物理學家塞西爾·鮑威爾等人通過對宇宙射線照相發現了質量約為電子靜止質量273倍的π介子，從而證實了湯川的預言。

微中子的發現

恩里科·費米

1914年詹姆斯·查兌克發現β衰變的譜線是連續譜，這表明在β衰變中存在一部分未知的能量損失。為此，沃爾夫岡·包立於1930年提出微中子假說：在β衰變過程中，伴隨每一個電子有一個輕的中性粒子一起被發射出來，包立當時將這種粒子稱作中子。但隨後查兌克於1932年發現了「真正」的大質量中子後，這種中性粒子後來被費米改成了現在具有義大利文風格的名字，稱作（反）微中子。1934年，費米在此基礎上將產生電子和微中子的過程和產生光子的過程進行了類比，提出中子和質子只是核子的兩種狀態，β衰變即這兩種狀態之間的躍遷過程，從中會釋放出電子和微中子；而相對於電磁交互作用釋放的光子，釋放電子和微中子的交互作用被稱作弱交互作用。義大利物理學家維克和漢斯·貝特後來用費米的衰變理論預言了第三種β衰變的形式：電子俘獲，這一預言後來也被實驗證實。1953年，洛斯阿拉莫斯國家實驗室的克萊德·科溫和弗雷德里克·萊因斯等人利用核反應爐的β衰變產生的反微中子對質子進行散射，通過測量得到的中子和正電子的散射截面直接證實了反微中子的存在。相關論文《自由微中子的探測：一個證實》於1956年發表在《科學》雜誌上，這一結果獲得了1995年的諾貝爾物理學獎。

夸克模型的建立

默里·蓋爾曼

如前所述，夸克模型是由蓋爾曼和喬治·茨威格在1964年分別獨立提出的，在他們的模型中，強子由三種味的夸克：上夸克、下夸克和奇夸克組成，這三種夸克決定了強子具有的電荷和自旋等屬性。物理學界對這個模型最初的意見是具有爭議的，包括爭論夸克是否是一種物理實在，還是只是為了解釋當時無法解釋的一些現象而提出的抽象概念。不到一年之後，美國物理學家謝爾登·格拉肖和詹姆斯·比約肯擴展了夸克模型，他們預言還有第四種味的夸克：魅夸克存在。這個預言能夠更好地解釋弱交互作用，使夸克數和當時已知的輕子數相等，並暗示了一個能夠給出已知介子的質量的質量公式。

1968年，在史丹佛直線加速器中心進行的非彈性電子散射實驗表明質子具有更小的點粒子結構，不是一種基本粒子。當時的物理學家並不傾向於將這些更小的粒子稱為夸克，而是按費曼的習慣稱之為部分子parton。後來這個實驗的產物被判斷為上夸克和下夸克，但部分子這一名稱仍被沿用至今，它被用於強子的組成部分的統稱（夸克、反夸克和膠子）。深度非彈性散射實驗還間接證實了奇夸克的存在，奇夸克的證實為1947年在宇宙射線中發現的K介子和π介子提供了解釋。1970年，格拉肖等人再次撰文論證了魅夸克的存在性。1973年，夸克的味增加到六種，這是由日本物理學家小林誠和益川敏英在實驗上觀察到CP破壞並認為這一對夸克可以對此加以解釋而提出的。這兩種新夸克被稱作頂夸克和底夸克。1974年11月，兩組團隊幾乎在同一時間觀測到了魅夸克，他們是伯頓·里克特領導的史丹佛直線加速器中心和丁肇中領導的布魯克海文國家實驗室。實驗中觀測到的魅夸克是和反魅夸克一起束縛在介子中的，而這兩個研究小組分別給了這種介子不同的符號標記：J和ψ，從而這種介子後來被稱作J/ψ介子。這個發現終於使夸克模型得到了物理學界的普遍公認 。1977年，費米實驗室的利昂·萊德曼領導的研究小組發現了底夸克，這為頂夸克的存在提供了強烈暗示。但直到1995年頂夸克才被費米實驗室的另一組研究團隊發現，

宇稱不守恆的發現

二十世紀五十年代人們在加速器實驗中觀測到為數眾多的「奇異粒子」，它們具有協同產生，非協同衰變的特性。蓋爾曼為此引入了一個新的量子數：奇異數，來解釋這一特性，即在強交互作用下奇異數守恆，而在弱交互作用下奇異數不守恆。其中在K介子的衰變過程中，人們發現有兩種質量、壽命和電荷都相同的粒子：θ介子和τ介子，它們唯一的區別是衰變後產物不同：一個衰變為兩個π介子，另一個衰變為三個π介子。其中π介子具有負的宇稱，從而衰變為兩個π介子意味著這種粒子具有正的宇稱，而衰變為三個則意味著有負的宇稱。如果宇稱守恆定律成立，則表明這兩種粒子雖然其他性質都相同卻不是同一種粒子，果真如此為何θ介子和τ介子的性質如此相同？這一難題當時被稱作θ-τ之謎。

1956年，當時在美國的物理學者李政道和楊振寧發表了著名論文《弱交互作用中的宇稱守恆質疑》，在這篇文章中他們認為，θ-τ之謎所帶來的宇稱不守恆問題不是一個孤立事件，宇稱不守恆很可能就是一個普遍性的基礎科學原理。在電磁交互作用及強交互作用中，宇稱確實守恆，因此在那時期的科學家猜想在弱交互作用中宇稱也守恆，但這一點尚未得到實驗驗證。李楊二人的理論研究結果顯示出，在弱交互作用中，宇稱並不守恆。他們提出了一個在實驗室中驗證宇稱守恆性的實驗方案。李政道隨即請求吳健雄對於這一點進行實驗驗證。吳健雄選擇了具有放射性的鈷-60樣品進行該實驗，成功證實了宇稱在弱交互作用中確實不守恆。
Θ+
和
τ+
後來被證明是同一種粒子，也就是K介子，
K+
。

宇稱不守恆是粒子物理學領域一項重要發現，其對於標準模型的建立非常重要。為了表彰李楊二人做出的理論貢獻，他們於1957年被授以諾貝爾物理學獎。

標準模型的建立

史蒂文·溫伯格

按美國物理學家史蒂文·溫伯格的說法，在五六十年代粒子物理學產生了三個「出色的想法」：蓋爾曼的夸克模型、1954年楊振寧和羅伯特·米爾斯將規範對稱性推廣至非阿貝爾群（楊-米爾斯理論）來解釋強交互作用和弱交互作用、自發對稱性破缺（希格斯機制）。二十世紀六十年代，人們對這些發展之間的聯繫有了更深刻的理解，謝爾登·格拉肖開始了將電磁理論和弱交互作用理論統一起來的嘗試。1967年，溫伯格和巴基斯坦物理學家阿卜杜勒·薩拉姆試圖在楊-米爾斯理論的基礎上將規範場論應用到強交互作用，但仍然遇到了楊-米爾斯理論無法解釋粒子的靜止質量在規範理論中為零及不可重整化等問題。後來溫伯格在反思中發現可以將規範場論應用到格拉肖的電弱理論中，因為在那裡可以引入自發對稱性破缺的希格斯機制，希格斯機制能夠為所有的基本粒子賦予非零靜止質量。結果證明這一理論非常之成功，它不僅能夠給出規範玻色子的質量，還能給出電子及其他輕子的質量。特別地，電弱理論還預言了一種可觀測的實純量粒子——希格斯玻色子。溫伯格和薩拉姆都認為這個理論應當是可重整化的，但他們沒有證明這一點。1973年歐洲核子研究組織（CERN）發現了中性流，後來史丹佛直線加速中心於1978年在電子-核子散射中觀測到了中性流的宇稱破缺，至此電弱理論被物理學界完全接受了。

電弱理論的成功重新喚起了人們對規範場論的研究興趣，1973年，美國物理學家戴維·格婁斯和他的學生弗朗克·韋爾切克，以及美國物理學家休·波利策發現了非阿貝爾規範場中的漸近自由性質。而他們也給出了對於觀察不到靜止質量為零的膠子的解釋：膠子如同夸克一樣，由於色荷的存在而受到色禁閉的約束從而無法獨立存在。在統合了電弱理論和量子色動力學的基礎上，粒子物理學建立了一個能夠描述除重力以外的三種基本交互作用及所有基本粒子（夸克、輕子、規範玻色子、希格斯玻色子）的規範理論——標準模型，二十世紀中葉以來高能物理的所有實驗成果都符合標準模型的預言。然而，標準模型不但無法將重力，以及近年來提出的暗物質與暗能量包含在內，它所預言的希格斯玻色子的存在還沒有確鑿的實驗證實，它也沒有解釋微中子振盪中的非零質量問題。2008年起在歐洲核子研究組織開始運行的大型強子對撞機的主要實驗目的之一，就是對希格斯玻色子的存在性進行驗證；2013年3月14日，歐洲核子研究組織發表新聞稿正式宣布探測到希格斯玻色子。

近代物理的其他發展

凝聚體物理學

費利克斯·布洛赫

凝聚體物理學成為了目前物理學最為活躍的領域之一。僅在美國，該領域的研究者就占到該國物理學者整體的近三分之一，凝聚體物理學部也是美國物理學會最大的部門。早期的凝聚體物理是基於古典或半古典理論的，例如在金屬電子論中服從波茲曼統計的自由電子氣體模型，後來包立在此基礎上引入了由費米和狄拉克各自獨立建立的費米-狄拉克統計使之成為一種半古典理論，建立了金屬電子的費米能階等概念；以及彼得·德拜改進了固體比熱容的愛因斯坦模型，建立了更符合實際情形的德拜模型。1912年，勞厄、威廉·亨利·布拉格爵士和其子威廉·勞倫斯·布拉格爵士從晶體的X射線繞射提出了晶格理論，這成為了晶格結構分析的基礎，也標誌著近代固態物理學的開端。

二十世紀二十年代量子力學的誕生使凝聚體物理學具有了堅實的理論基礎，其立竿見影的成果是海森堡在1928年建立了鐵磁性的量子理論，不過對固態物理學界更有影響力的是同年他的學生、美籍瑞士裔物理學家費利克斯·布洛赫建立的能帶理論。雖然布洛赫是海森堡的學生，他建立能帶理論的基礎卻是薛丁格方程式。他從薛丁格方程式的解得到啟發，推導出在週期勢場中運動電子的波函數是一個調幅平面波，調幅因子（布洛赫波包）具有和晶格勢場相同的週期性，這一定理後來被稱作布洛赫定理。布洛赫的能帶理論解釋了很多以往固態物理學無法解釋的現象，如金屬電阻率、正霍爾係數等，後來在英國物理學家A.H.威爾遜、法國物理學家萊昂·布里元等人的完善下，能帶理論還進一步解釋了金屬的導電性、提出了費米面的概念，它對二十世紀三十年代的凝聚體物理學影響非常深遠。第二次世界大戰後，能帶理論在實際應用中發揮了重要作用，貝爾實驗室的威廉·肖克利、約翰·巴丁等人於1947年12月23日製造出世界上第一隻電晶體。

凝聚體物理學發展的另一個活躍領域是低溫方向：1911年，荷蘭物理學家卡末林·昂內斯發現水銀在4.2K的低溫時電阻率消失為零，這被稱作超導電性。對超導電性本質的解釋始終是物理學家難以解決的一個問題，即使是在布洛赫建立能帶理論之後。1933年，德國物理學家瓦爾特·邁斯納在實驗中發現超導體內部的磁場總保持為零，這被稱作邁斯納效應。人們從中發現，超導體的這種完全抗磁性實際來自固體本身的一種熱力學態，這種熱力學態正是具有超導電性和完全抗磁性這兩種屬性。為了進一步解釋超導電性，人們曾提出過一系列唯象理論，如二流體模型（戈特、亨德里克·卡西米爾，1934年）、倫敦方程式（屬於古典電動力學理論，倫敦兄弟，1935年）、金茲堡-朗道方程式（金茲堡、朗道，1950年）。直到1956年，美國物理學家利昂·庫珀利用量子場論方法建立了庫珀對的概念，當電子能量低於費米能時，庫珀對由兩個動量和自旋都大小相等方向相反的電子結合而形成。1957年，庫珀和巴丁、約翰·施里弗三人在此基礎上共同提出了超導的微觀理論，又稱作BCS理論，至此在微觀上解釋了超導電性。1962年，劍橋大學的布賴恩·約瑟夫森應用BCS理論計算出基於量子隧道效應的約瑟夫森效應。

當代天體物理學

卡爾·史瓦西

天體物理學是一門相當新近發展的科學領域。在十九世紀，研究重心逐漸從天文學轉變至天體物理學，這可以歸功於三項重要科技突破：幾何視差、光譜學與天體攝影。使用幾何視差方法，天體物理學者可以準確地測量恆星距離。光譜學技術的發展使得檢試天體的物理與化學性質成為可能。天體攝影增進天文學者通過可見光觀測與探索天體現象的能力。這些突破加上新一代望遠鏡，以及對於包括量子力學、廣義相對論在內的基本科學的深切了解，導致了二十世紀天體物理學的快速發展。

愛因斯坦建立廣義相對論之初，由於場方程式的複雜性他一時還無法找到場方程式的任何一種精確解。在他研究水星近日點進動的問題中，他在近似計算了無轉動無電荷的球形質量的重力場。然而就在廣義相對論建立的同時，1915年12月德國物理學家卡爾·史瓦西給了他一個驚喜，史瓦西使用了球坐標求得了這個問題的精確解。史瓦西解預言了在重力場非常強的情形下光也無法逸出的可能性，從而在理論上證明了黑洞的存在。。1930年，印度物理學家蘇布拉馬尼揚·錢德拉塞卡根據廣義相對論計算出質量大於1.4倍太陽質量（錢德拉塞卡極限）的非轉動星體會因重力塌縮成為電子簡併態。愛丁頓雖然在理論上支持黑洞存在的可能性，但同時認為錢德拉塞卡的觀點事實上不能成立，他認為「應當有某種自然定律阻止恆星出現這種荒唐的行為」。當時的物理學家如波耳、亨利·羅素等人都贊同錢德拉塞卡的理論，但出於愛丁頓聲望的原因，他們並沒有公開對錢德拉塞卡表示支持。不過從某種意義上說，愛丁頓也是正確的，當恆星質量大於錢德拉塞卡極限後，確實仍然會有中子簡併壓力阻止恆星繼續塌縮。到了1939年，美國物理學家羅伯特·歐本海默等人推算了這種情形的恆星質量上限，這個極限被稱作托爾曼-歐本海默-沃爾科夫極限（1.5至3倍太陽質量）。當今的天體物理學家普遍認為，除非有如未知的夸克簡併壓力一類因素的存在，質量大於托爾曼-歐本海默-沃爾科夫極限的恆星將最終會塌縮為錢德拉塞卡所預言的黑洞。即使如此，史瓦西解作為當時能夠描述黑洞行為的唯一精確解，由於具有一些讓人看似不大優美的性質（如$r=2M\,$處的坐標奇異點）以及難以與實驗觀測相聯繫，一直沒有進入主流物理學研究的視野，關於黑洞的理論乃至整個廣義相對論領域的研究由此擱置了二十年之久。

拉塞爾·赫爾斯

直到1958年，美國物理學家大衛·芬克爾斯坦從史瓦西度規中引入了視界的概念，並建立了相應的愛丁頓-芬克爾斯坦坐標系，證明了$r=2M\,$處的坐標奇異點本身不具有真正意義的奇性。1963年，紐西蘭物理學家羅伊·克爾得到了場方程式在旋轉黑洞情形的精確解——克爾度規，並證明克爾黑洞具有幾何上環狀的奇異點；1964年，英國物理學家羅傑·潘洛斯和史蒂芬·霍金全局幾何的基礎上提出了著名的關於黑洞的潘洛斯–霍金奇性定理，指出任何有質量的實體發生重力塌縮並達到一個特定階段後都會形成奇異點。1967年，天文學家在實驗上發現了脈衝星，並隨之證明了脈衝星是在高速旋轉的中子星，直到此時中子星才真正從理論中脫離，成為了被人們承認的實在。中子星的發現使人們的興趣轉移回這些重力塌縮導致的高緻密天體上，這時的廣義相對論才真正進入了理論物理和天體物理主流研究的視野，這一時期（1960年至1975年）被稱作廣義相對論的黃金時代。在十幾年中廣義相對論給天體物理學帶來了無數豐厚的成果，包括重力時間延遲效應（歐文·夏皮羅，1960年）、克爾度規（克爾，1963年）、潘洛斯圖（潘洛斯、卡特，1963年）、奇異點定理（潘洛斯、霍金，1964年）、中子星的不穩定模式（錢德拉塞卡，1965年）、正則量子重力（德威特，1967年）、無毛定理（1967年）、參數化後牛頓形式（1967年）、宇宙審查假說（較弱的版本，潘洛斯，1969年）、潘洛斯過程（潘洛斯，1969年）、黑洞面積定理（霍金，1969年）、克魯斯卡爾-塞凱賴什坐標系（馬丁·克魯斯卡爾、喬治·塞凱賴什，1970年）、黑洞熱力學（雅各布·貝肯斯坦、卡特、霍金，1972年）、赫爾斯-泰勒脈衝雙星（PSR 1913+16，拉塞爾·赫爾斯、約瑟夫·泰勒，1974年）、霍金輻射（霍金，1974年）等。

在實驗觀測方面，二十世紀天體物理學的重要進展在於擴展了觀測的電磁波譜，觀測手段的進步使觀測天文學從原有的可見光觀測擴展到基於無線電、微波、紅外線、紫外線、X射線和伽瑪射線的完整電磁波譜觀測。1931年，貝爾實驗室的卡爾·央斯基用天線陣接收到了來自銀河系中心的無線電波。隨後美國天文學家格羅特·雷伯在自家的後院建造了一架口徑9.5米的天線，並在1939年接收到了來自銀河系中心的無線電波，並且於1941年根據觀測結果繪製了第一張無線電天圖。無線電天文學的建立極大地開闊了人們觀測宇宙的窗口，其著名成果就是二十世紀六十年代天文學的四大發現：脈衝星、類星體、宇宙微波背景輻射和星際有機分子。其中貝爾實驗室的阿諾·彭齊亞斯和羅伯特·威爾遜於1965年發現的宇宙微波背景輻射更是對大爆炸理論具有非常重要的意義。在傳統的電磁波天文學之外，赫爾斯和泰勒於1974年發現的脈衝雙星PSR1913+16則揭開了現代重力波天文學觀測的序幕，他們對PSR1913+16長達三十年的觀測結果表明這一對脈衝雙星正如廣義相對論所精確預言的那樣在進行重力輻射。這項工作不僅是對廣義相對論的直接驗證，也是人們首次實現的對重力波的間接觀測。除像黑洞這樣不會產生任何古典電磁輻射的天體外，現代宇宙模型表明宇宙中還存在比例高達96%的不輻射任何電磁波的暗物質和暗能量，有希望對這些天體進行直接觀測正是發展重力波天文學的重要意義之一。

宇宙學

埃德溫·哈伯

物理意義上的宇宙學是從廣義相對論的建立才真正開始的。在此之前，宇宙在人們頭腦中的觀念是靜態且無限的，德國天文學家海因里希·奧伯斯因此提出了著名的奧伯斯悖論。1917年愛因斯坦將廣義相對論應用於整個宇宙，發表了標誌著物理宇宙學建立的論文《根據廣義相對論對宇宙學所做的考察》。考慮到同時期的宇宙學研究中靜態宇宙的學說仍被廣為接受，愛因斯坦在場方程式中添加了一個新的常數，這被稱作宇宙常數項，以求得和當時的「觀測」相符合。然而，場方程式所預言的宇宙並不是靜態的：1922年蘇聯物理學家亞歷山大·傅里德曼將廣義相對論應用至流體力學，從場方程式推導出了傅里德曼方程式。而比利時牧師、物理學家喬治·勒梅特在1927年利用傅里德曼方程式給出了第一個膨脹宇宙模型的解，這個解後來被稱作傅里德曼-勒梅特-羅伯遜-沃克度規。勒梅特提出了宇宙在不斷膨脹並起源於一個「原生原子」的爆炸的觀點，這成為現代大爆炸理論的雛形。1929年，美國天文學家埃德溫·哈伯通過實驗支持了勒梅特的觀點，哈伯證明了觀測到的旋渦星雲實質屬於星系，並通過觀測造父變星測量了這些星系的距離。他得出了星系的紅移和光度之間的關係，並將它解釋為哈伯定律：星系在各個方向上都在退行，其相對地球的退行速度大小正比於它們距地球的距離。

史蒂芬·霍金

考慮到宇宙學原理：宇宙在大尺度上是均一且各向同性的，哈伯定律意味著宇宙正在膨脹。雖然在第二次世界大戰結束後膨脹宇宙的事實已經基本得到公認，卻仍然存在兩種截然不同的理論來描述宇宙：一種是勒梅特的「爆炸」假說，這一理論後來被美籍俄裔物理學家喬治·伽莫夫支持並發展，伽莫夫提出宇宙起源於高溫高密的原始物質，他和他的學生拉爾夫·阿爾菲提出了大爆炸核合成的理論（在阿爾菲1948年提交的論文《化學元素的起源》中，伽莫夫說服了漢斯·貝特把他的名字署在了論文上，又把自己的名字署在最後，這樣三個人的名字恰好代表著前三個希臘字母α、β、γ。這份標誌宇宙大爆炸模型的論文以阿爾菲、貝特、伽莫夫三人的名義在1948年4月1日愚人節那天發表，稱為αβγ理論），阿爾菲和羅伯特·赫爾曼還預言了殘餘的背景輻射的存在；另一種是英國天文學家弗雷德·霍伊爾、托馬斯·戈爾德和赫爾曼·邦迪創立的穩態宇宙模型，這種模型認為隨著宇宙的膨脹，新的物質會不斷創生，從而使宇宙在任何時候看起來各處都相同。長久以來這兩種觀點的受支持程度都不相上下，1949年3月霍伊爾在BBC的廣播節目中首次將勒梅特和伽莫夫等人的理論稱作「這個大爆炸的觀點」（this Big Bang idea），這成為了這一理論名稱的由來。不過，二十世紀六十年代發現的遙遠的類星體和無線電星系開始成為不支持穩恆態宇宙模型的證據，而1965年阿諾·彭齊亞斯和羅伯特·威爾遜發現的宇宙微波背景輻射明確反駁了穩恆態理論。大爆炸理論由此被認為是最能解釋宇宙起源和演化的理論，唯一讓物理學家不滿的是其中奇異點的存在。後來，潘洛斯和霍金的奇異點定理證明了奇異點的存在是廣義相對論的必然結果，這使得大多數物理學家都接受了大爆炸理論，並認為我們所觀測到的宇宙起源於一個有限的時間。

二十世紀九十年代，大爆炸理論得到了宇宙學實驗觀測的有力驗證。隨著幾個重要的空間望遠鏡：宇宙背景探測者、哈伯太空望遠鏡和威爾金森微波各向異性探測器的發射和數據採集，物理學家有能力對大爆炸理論中的參數進行精確的測量。不僅如此，他們還意外地發現宇宙的膨脹速度在不斷增長：愛因斯坦曾經將他引入的宇宙常數項稱為「他一生中的最大錯誤」，然而實驗觀測表明宇宙常數項仍然是有用的：為了解釋宇宙的加速膨脹，物理學家結合對相關超新星的觀測提出了暗物質和暗能量理論。當今宇宙學最為認可的模型——ΛCDM模型——結合了宇宙微波背景輻射、宇宙大尺度結構和宇宙加速膨脹，這是能夠構建一個自洽的物理宇宙模型的最簡單的假設。

萬有理論

基本粒子的標準模型

從伽利略的時代算起，物理學發展的四百多年歷史中已經經歷了幾次大的統一：牛頓統一了「天上的」和「地上的」力學，馬克士威統一了電磁理論，格拉肖等人統一了弱交互作用和電磁交互作用。而嘗試將電弱交互作用和強交互作用統一起來的理論統稱為大一統理論，大一統理論將統一標準模型中的四種規範玻色子和傳遞強交互作用的八種膠子規範玻色子。當前被建議的大一統理論有很多，一般來說這些理論都做出了如下的關鍵性預言：磁單極子、宇宙弦、質子衰變等，時至今日還沒有上述的任何一種現象得到實驗的證實。如要通過實驗驗證大一統理論，粒子所需的能量要達到～10¹⁶GeV，這已經遠遠超過現有的任何粒子加速器所能達到的範圍。

在大一統理論以外，還存在著如何將重力納入量子理論的問題。二十世紀中葉之前愛因斯坦等人所做的古典統一場論工作試圖在古典理論的框架下將電磁場和重力場統一起來，事實證明這些理論都是不成功的。標準模型中沒有描述萬有引力交互作用，在現有的量子場論手段下重力場的量子化會帶來不可重整化；而物質的量子化和時空的幾何化兩者沒有任何相容性，廣義相對論中不可避免地有曲率無窮大的微觀奇異點存在，這些情況都要求有一個量子化的重力理論的建立。根據估計，對於這樣一個能夠將大一統理論和重力理論統一起來的萬有理論，實驗驗證所需的能量將達到普朗克能量的量級：10¹⁹百萬電子伏特。

萬有理論

萬有引力交互作用

電核交互作用（大一統理論）

強交互作用 SU(3)

電弱交互作用 SU(2)×U(1)

弱交互作用 SU(2)

電磁交互作用 U(1)

電力

磁力

愛德華·維騰

當前被提議的主流萬有理論是超弦理論及M理論；而對圈量子重力的研究可能也會對建立萬有理論產生基礎性的影響，但這並不是圈量子重力論的主要目標。弦理論的雛形起源於1968年，麻省理工學院的義大利物理學家加布里埃萊·韋內齊亞諾發現用Β函數描述強交互作用粒子的散射振幅時正滿足強交互作用粒子所具有的對偶性。後來人們發現這個函數能夠被解釋為弦與弦之間的散射振幅，從而這個數學公式就成為了弦理論的起源。猶太裔美國物理學家約翰·施瓦茨是現代弦論的創始人之一，他自1972年起開始研究弦論，並由於和英國物理學家麥可·格林合作研究的I型弦理論中的反常相消而引發了所謂第一次超弦革命。在1984年至1986年間發生的第一次超弦革命中，弦論正式開始流行，物理學家認識到弦論能夠描述所有的基本粒子以及彼此間的交互作用，從而期望弦論能夠成為一種終極理論：歐洲核子研究組織的約翰·埃利斯就是由此提出了「萬有理論」一詞 。第二次超弦革命是在1994年至1997年間，其影響更為深遠。1995年美國數學物理學家愛德華·維騰猜測在強耦合極限下十維的超弦、以及廣義相對論與超對稱的統一即所謂超重力，能夠構成一個猜想的十一維模型的一部分，這種模型在施瓦茨的建議下被叫做M理論。同年十月，加利福尼亞大學聖塔芭芭拉分校的約瑟夫·波爾欽斯基發現超弦理論中產生的孤子正是他們於1989年發現的D-膜。

參見

• 光學史
• 科學史、物理學
• 物理學家列表
  • 諾貝爾物理學獎得主列表