圆 (英語:Circle ),根據歐幾里得 的《几何原本 》定義,是在同一平面 内到定点的距离等于定长的点的集合[ 1] [ 2]
古代人最早是从太阳 、阴历十五的月亮 得到圆的概念的。在一万八千年前的山顶洞人 曾经在兽牙 、砾石 和石珠上钻孔,那些孔有的就很像圆。[ 3] 陶器时代 ,许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。[ 4] 石纺锤 或陶纺锤 。古代人还发现搬运圆的木头时滚着走比较省劲。后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走。[ 5]
约在6000年前,美索不达米亚 人,做出了世界上第一个轮子——圆型的木盘。[ 4] 埃及 人认为:圆,是神赐给人的神圣图形。一直到两千多年前中国的墨子 (约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。意思是说:圆有一个圆心 ,圆心到圆周 上各点的距离(即半径 )都相等。[ 4] 欧几里得 (约公元前330-前275年)给圆下定义要早100年。
直角坐标系 中的定义:
(
x
−
x
m
)
2
+
(
y
−
y
m
)
2
=
a
2
{\displaystyle (x-x_{m})^{2}+(y-y_{m})^{2}=a^{2}}
(
x
m
,
y
m
)
{\displaystyle (x_{m},y_{m})}
参数方程 的定义:
x
=
x
m
+
a
cos
θ
{\displaystyle x=x_{m}+a\cos \theta }
y
=
y
m
+
a
sin
θ
{\displaystyle y=y_{m}+a\sin \theta }
极坐标 方程 的定义(圆心在原点):
r
=
a
{\displaystyle r=a}
圆是在同一平面内到定点的距离等于定长的点的集合,这个定点叫做圆的圆心(通常用
O
{\displaystyle O}
[ 6]
圆周上任何两点相连的线段 称为圆的弦 (英語:chord )。如图2,
A
{\displaystyle A}
B
{\displaystyle B}
A
B
¯
{\displaystyle {\overline {AB}}}
弦
圆周上任意两点 间的部分叫做弧 (英語:arc ),通常用符号
⌢
{\displaystyle \frown }
[ 6]
直径(英語:diameter ):经过圆心的弦 叫做直径(用
d
{\displaystyle d}
[ 2]
半径(英語:radius ):在圆中,连接圆心和圆上任意一点的线段叫做圆的半径,半径用字母
r
{\displaystyle r}
k
=
{
X
∈
E
∣
M
X
¯
<=
r
}
{\displaystyle k=\{X\in E\mid {}{\overline {MX}}<=r\}}
假如一条直线与圆相交僅有一个交点,那么称这条直线是这个圆的切线 ,与圆相交的点 叫做切点。如[ 2] 直线
Q
P
¯
{\displaystyle {\overline {QP}}}
P
{\displaystyle P}
Q
P
¯
{\displaystyle {\overline {QP}}}
切线 。
过圆上一点的切线:设该点为
P
(
x
o
,
y
o
)
{\displaystyle P(x_{o},y_{o})}
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
(
x
o
−
a
)
(
x
−
a
)
+
(
y
o
−
b
)
(
y
−
b
)
=
r
2
{\displaystyle (x_{o}-a)(x-a)+(y_{o}-b)(y-b)=r^{2}}
性质定理:圆的切线垂直于经过切点的半径。
推论1:经过圆心且垂直于切线 的直线 必经过切点。
推论2:经过切点且垂直于切线的直线必经过圆心。
一条直线 与一条弧线有两个公共点,这条直线是这条曲线的割线(英語:Secant Theorem )。[ 2]
Q
O
¯
{\displaystyle {\overline {QO}}}
直线
Q
O
¯
{\displaystyle {\overline {QO}}}
θ 的正割是从O到Q的距离.
圆的一周的长度称为圆的周长 (记作
C
{\displaystyle C}
C
=
π
d
{\displaystyle C=\pi d}
C
=
2
π
r
{\displaystyle C=2\pi r}
其中
π
{\displaystyle \pi }
圆周率 。
圆的面积 与半径的关系是:
A
=
π
r
2
{\displaystyle A=\pi r^{2}}
圆既是轴对称图形 又是中心对称图形 ,圆的对称轴为经过圆心
O
{\displaystyle O}
直线 ,圆的对称中心为圆心
O
{\displaystyle O}
[ 6]
图2:弦、圆周角、圆心角 圆心角:顶点 在圆心的角 叫圆心角,圆心角的度数等于它所对的弧的度数,公式表示为
θ
=
L
2
π
r
⋅
2
π
=
L
r
{\displaystyle \theta ={\frac {L}{2\pi r}}\cdot 2\pi ={\frac {L}{r}}}
[ a] [ 2]
M
{\displaystyle M}
∠
A
M
B
{\displaystyle \angle AMB}
圆周角:顶点 在圆周上,角 两边和圆相交的角叫圆周角。如右图,
∠
A
C
B
{\displaystyle \angle ACB}
C
{\displaystyle C}
∠
A
C
B
{\displaystyle \angle ACB}
A
C
¯
{\displaystyle {\overline {AC}}}
B
C
¯
{\displaystyle {\overline {BC}}}
∠
A
C
B
{\displaystyle \angle ACB}
同圆或等圆中,相等的圆心角所对的弦 相等,所对的弧 相等,弦心距[ b] [ 6]
圆周角定理:同弧所对的圆周角等于它所对的圆心的角 的一半。[ 6]
M
{\displaystyle M}
A
,
B
,
C
{\displaystyle A,B,C}
点 ,那麼:
∠
A
M
B
=
2
∠
A
C
B
{\displaystyle \angle AMB=2\;\angle ACB}
证明:
∵
B
M
=
C
M
,
A
M
=
C
M
{\displaystyle \because BM=CM,AM=CM}
∵
∠
B
C
M
=
∠
C
B
M
,
∠
A
C
M
=
∠
C
A
M
{\displaystyle \because \angle BCM=\angle CBM,\angle ACM=\angle CAM}
∴
∠
B
M
S
=
∠
B
C
M
+
∠
C
B
M
{\displaystyle \therefore \angle BMS=\angle BCM+\angle CBM}
∵
∠
A
M
S
=
∠
A
C
M
+
∠
C
A
M
{\displaystyle \because \angle AMS=\angle ACM+\angle CAM}
∴
∠
B
M
S
+
∠
A
M
S
=
2
(
∠
B
C
M
+
∠
A
C
M
)
{\displaystyle \therefore \angle BMS+\angle AMS=2(\angle BCM+\angle ACM)}
即:
∠
A
M
B
=
2
∠
A
C
B
{\displaystyle \angle AMB=2\;\angle ACB}
圆周角定理的推论:
同弧或等弧 所对的圆周角相等;同圆或等圆中,相等的圆周角 所对的弧是等弧。
半圆或直径所对的圆周角是直角 ;圆周角是直角 所对的弧的半圆,所对的弦是直径。
若三角形 一边上的中线 等于这边的一半,那么这个三角形是直角三角形 。
垂径定理示意图 垂径定理:垂直于弦 的直径平分弦且平分弦所对的弧 。[ 1]
B
E
¯
⊥
{\displaystyle {\overline {BE}}\perp }
A
C
¯
{\displaystyle {\overline {AC}}}
B
E
¯
{\displaystyle {\overline {BE}}}
A
C
¯
{\displaystyle {\overline {AC}}}
A
C
⌢
{\displaystyle {\overset {\frown }{AC}}}
推论1:(1)平分弦 [ c] 弧 。 (2)弦 的垂直平分线 经过圆心,并且平分弦所对的两条弧。
(3)平分弦 所对的一条弧 的直径,垂直平分弦,并且平分弦所对的另一条弧
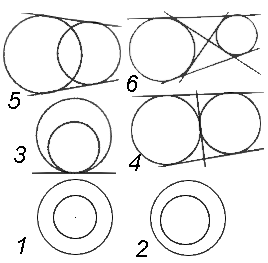
兩個不同大小的圓(半徑分別為
r
{\displaystyle r}
R
{\displaystyle R}
d
{\displaystyle d}
r
<
R
{\displaystyle r<R}
[ 2]
d
=
0
{\displaystyle d=0}
同心圓 。
0
<
d
<
R
−
r
{\displaystyle 0<d<R-r}
d
=
R
−
r
{\displaystyle d=R-r}
d
=
R
+
r
{\displaystyle d=R+r}
R
−
r
<
d
<
R
+
r
{\displaystyle R-r<d<R+r}
d
>
R
+
r
{\displaystyle d>R+r}
在解析几何中,符合特定条件的某些圆构成一个圆系 ,一个圆系所具有的共同形式的方程称为圆系方程。例如求半径到直线距离的方程就可以叫圆系方程。 [ 2]
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
(
a
,
b
)
{\displaystyle (a,b)}
r
{\displaystyle r}
同心圆 的圆系方程 .若
r
{\displaystyle r}
a
{\displaystyle a}
b
{\displaystyle b}
x
{\displaystyle x}
y
{\displaystyle y}
过两圆
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
=
0
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}=0}
x
2
2
+
y
2
2
+
D
2
x
+
E
2
y
+
F
2
=
0
{\displaystyle x_{2}^{2}+y_{2}^{2}+D_{2}x+E_{2}y+F_{2}=0}
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
+
⋏
(
x
2
2
+
y
2
2
+
D
2
x
+
E
2
y
+
F
2
)
=
0
(
⋏
≠
−
1
)
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}+\curlywedge (x_{2}^{2}+y_{2}^{2}+D_{2}x+E_{2}y+F_{2})=0(\curlywedge \neq -1)}
过直线
A
x
+
B
y
+
C
=
0
{\displaystyle Ax+By+C=0}
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
=
0
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}=0}
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
+
⋏
(
A
x
+
B
y
+
C
)
=
0
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}+\curlywedge (Ax+By+C)=0}
过两圆
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
=
0
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}=0}
x
2
2
+
y
2
2
+
D
2
x
+
E
2
y
+
F
2
=
0
{\displaystyle x_{2}^{2}+y_{2}^{2}+D_{2}x+E_{2}y+F_{2}=0}
x
1
2
+
y
1
2
+
D
1
x
+
E
1
y
+
F
1
−
(
x
2
2
+
y
2
2
+
D
2
x
+
E
2
y
+
F
2
)
=
0
{\displaystyle x_{1}^{2}+y_{1}^{2}+D_{1}x+E_{1}y+F_{1}-(x_{2}^{2}+y_{2}^{2}+D_{2}x+E_{2}y+F_{2})=0}
椭圆 是平面 上到两个固定点的距离之和为常数 的点之轨迹,椭圆的形状可以用离心率 来表示;圆可以看作是一种特殊的椭圆,即当椭圆的两个焦点 重合,离心率
ε
=
0
{\displaystyle \varepsilon =0}
在三維空間 ,球面被設定為是在
R
3
{\displaystyle R^{3}}
r
{\displaystyle r}
點 的集合,此處r是一個正的實數 ,稱為半徑,固定的點稱為球心或中心,並且不屬於球面的範圍。
r
=
1
{\displaystyle r=1}
在測度空間 中,圓的定義仍舊指距離一定點等距(在該測度下)的點的集合 。
截面 為圓的三維 形狀 有:
當多邊形的每條邊固定,以有外接圓的圖形面积 最大。[ 7]
^ L为扇形 弧 长,变形公式
L
=
r
⋅
θ
{\displaystyle L=r\cdot \theta }
^ 弦心距指的是圆心 到弦 的距离
^ 不是直径