隨機變數

隨機變數是一種數學概念，用來表示隨機試驗結果的變數。

「random variable」的各地常用譯名
中國大陸	隨機變量
臺灣	隨機變數
港澳	隨機變數
日本	確率変数
韓國	確率變數

簡介

隨機變數通常用大寫字母$X$、$Y$表示。在各種隨機試驗中，每一個隨機事件都可以用一個變數代替任何一個數值。例如擲骰子時擲出的點數是1,2,..,6中的一個，其中的任意一個點數都可以用變數$X$來表示，$X$可以=1，=2....=6，又例如在產品的抽查中，抽到正品可以用「$X$=1」來表示，抽到次品可以用「$X$=0」來表示，這樣$X$又可以=1也可以=0。，隨機變數實質上是函式。稱其為變數是指可作為應變數。

正式定義

隨機變數的定義 — $X:S\to \mathbb {R}$ 是一個定義在樣本空間 $S$ 上的實函式，而 ${\mathcal {E}}\subseteq {\mathcal {P}}(S)$ 為 $S$ 的某事件族，若對任意實數 $r\in \mathbb {R}$ ，有：

$\{s\in S\,|\,X(s)\leq r\}\in {\mathcal {E}}$

（也就是說，$X(s)\leq r$ 必為一個事件）

則稱函式 $X$ 為一個（在 ${\mathcal {E}}$ 的意義下）定義在 $S$ 上的隨機變數。

直觀上，隨機變數為一種特殊的實函式，其值不大於某數的狀況都是事件。所以一個函式是不是隨機變數也跟「怎樣的子集合算事件」有密不可分的關係。

如果隨機變數 $X$ 的取值是有限的或者是可數無窮盡的值：

$X(S)=\{x_{1},x_{2},x_{3},\ldots ,\}\cong \mathbb {N}$

則稱 $X$ 為離散隨機變數。如果 $X$ 的取值遍布一區間甚至是整個數線：（$a,\,b\in \mathbb {R}$）

$X(S)=[a,\,b]$

則稱$X$為連續隨機變數。

與可測函式的關係

如果取 ${\mathcal {I}}$ 為所有實開區間所構成的集合：

${\mathcal {I}}={\bigg \{}A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists a)(\exists b)\left[\,(a,\,b\in \mathbb {R} )\wedge (A=(a,\,b))\,\right]{\bigg \}}$

則可以把鮑萊耳代數 ${\mathcal {B}}$ 定義為包含 ${\mathcal {I}}$ 的最小Σ-代數：

${\mathcal {B}}:=\sigma ({\mathcal {I}})=\bigcap {\bigg \{}\Sigma \,{\bigg |}\,(\Sigma {\text{ is a sigma algebra.}})\wedge ({\mathcal {I}}\subseteq \Sigma ){\bigg \}}$

則根據阿基米德性質，對任意實數 $r\in \mathbb {R}$ ，$(-\infty ,\,r]\in {\mathcal {B}}$，有以下的關係：

$(r,\,\infty )=\bigcup \left\{A\in {\mathcal {I}}\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(r,\,n)\right]\right\}$

$(-\infty ,\,r]=\mathbb {R} -(r,\,\infty )$

反之，也可以用類似的方法，由任意的 $(-\infty ,\,r]$ ，透過聯集和補集組合出 $(a,\,b)$：

$(-\infty ,\,b)=\bigcup \left\{A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(-\infty ,\,b-{\frac {1}{n}}]\right]\right\}$

$(a,\,b)=\left(\mathbb {R} -(-\infty ,\,a]\right)\cup (-\infty ,b)$

這樣的話，任意的 $r\in \mathbb {R}$ 都有$\{s\in S\,|\,X(s)\leq r\}\in {\mathcal {E}}$ ，等價於對任意的 $a,\,b\in \mathbb {R}$ 都有 $\{s\in S\,|\,a<X(s)<b\}\in {\mathcal {E}}$，這樣根據可測函式性質的定理(2)，上小節定義的 $X$ ，就是一個 ${\mathcal {E}}$ - ${\mathcal {B}}$ 可測函式，換句話說，隨機變數是可測函式的一種特例。

範例

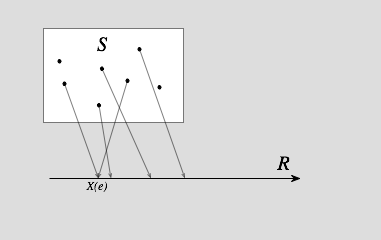實數坐標軸上的隨機變數示意圖

隨機擲兩個骰子，整個樣本空間由36個元素組成：

$S=\left\{(i,j)\in \mathbb {N} ^{2}|(i\leq 6)\wedge (j\leq 6)\right\}$

然後可以簡單地把 $S$ 的任意子集合都視為事件，換句話說，把事件族 ${\mathcal {E}}$ 取成 $S$ 的冪集：

${\mathcal {E}}={\mathcal {P}}(S)$

這樣的話，可以構造出許多定義在 $S$ 上的隨機變數，比如 $X$ 可以定義為「兩個骰子的點數和」；者 $Y$ 可以定義為「兩個骰子的點數差」：

$X(i,j):=i+j$

$Y(i,j):=|i-j|$

因為「兩個骰子的點數和不大於 $r$」和「兩個骰子的點數差不大於 $r$」的樣本點所構成的集合，都是 $S$ 的子集合，所以 $X$ 和 $Y$ 都是（在 ${\mathcal {E}}={\mathcal {P}}(S)$ 的意義下）定義在 $S$ 上的隨機變數，而且它們都是離散隨機變數。

性質

不確定性

隨機變數在不同的條件下由於偶然因素影響，其可能取各種隨機變數不同的值，具有不確定性和隨機性，但這些取值落在某個範圍的機率是一定的，此種變數稱為隨機變數。隨機變數可以是離散型的，也可以是連續型的。如分析測試中的測定值就是一個以機率取值的隨機變數，被測定量的取值可能在某一範圍內隨機變化，具體取什麼值在測定之前是無法確定的，但測定的結果是確定的，多次重複測定所得到的測定值具有統計規律性。隨機變數與模糊變數的不確定性的本質差別在於，後者的測定結果仍具有不確定性，即模糊性。

基本類型

簡單地說，隨機變數是指隨機事件的數量表現。某地若干名男性健康成人中，每人血紅蛋白量的測定值；等等。另有一些現象並不直接表現為數量，例如人口的男女性別、試驗結果的陽性或陰性等，但我們可以規定男性為1，女性為0，則非數量標誌也可以用數量來表示。這些例子中所提到的量，儘管它們的具體內容是各式各樣的，但從數學觀點來看，它們表現了同一種情況，這就是每個變數都可以隨機地取得不同的數值，而在進行試驗或測量之前，我們要預言這個變數將取得某個確定的數值是不可能的。 按照隨機變數可能取得的值，可以把它們分為兩種基本類型：

離散型隨機變數

即在一定區間內變數取值為有限個，或數值可以一一列舉出來。例如某地區某年人口的出生數、死亡數，某藥治療某病病人的有效數、無效數等

連續型隨機變數

即在一定區間內變數取值有無限個，或數值無法一一列舉出來。例如某地區男性健康成人的身長值、體重值，一批傳染性肝炎患者的血清轉氨酶測定值等。

詳細分析

表示方法

隨機試驗結果的量的表示。例如擲一顆骰子出現的點數，電話交換台在一定時間內收到的呼叫次數，隨機抽查的一個人的身高，懸浮在液體中的微粒沿某一方向的位移，等等，都是隨機變數的實例。 一個隨機試驗的可能結果（稱為基本事件）的全體組成一個基本空間$\Omega$（見機率）。隨機變數$X$是定義於$\Omega$上的函式，即對每一基本事件$\omega \in \Omega$，有一數值$X(\omega )$與之對應。以擲一顆骰子的隨機試驗為例，它的所有可能結果，共6個，分別記作$\omega _{1}$, $\omega _{2}$, $\omega _{3}$, $\omega _{4}$, $\omega _{5}$, $\omega _{6}$，這時，$\Omega =\{\omega _{1},\omega _{2},\omega _{3},\omega _{4},\omega _{5},\omega _{6}\}$，而出現的點數這個隨機變數$X$，就是$\Omega$上的函式$X(\omega k)=k$，$k=1,2,\ldots ,6$。又如設$\Omega =\{\omega _{1},\omega _{2},\ldots ,\omega _{n}\}$是要進行抽查的$n$個人的全體，那麼隨意抽查其中一人的身高和體重，就構成兩個隨機變數$X$和$Y$，它們分別是$\Omega$上的函式：$X(\omega k)=$「$\omega k$的身高」，$Y(\omega k)=$「$\omega k$的體重」，$k=1,2,\ldots ,n$。一般說來，一個隨機變數所取的值可以是離散的（如擲一顆骰子的點數隻取1到6的整數，電話台收到的呼叫次數隻取非負整數），也可以充滿一個數值區間，或整個實數軸（如液體中懸浮的微粒沿某一方向的位移）。

研究方法

在研究隨機變數的性質時，確定和計算它取某個數值或落入某個數值區間內的機率是特別重要的。因此，隨機變數取某個數值或落入某個數值區間這樣的基本事件的集合，應當屬於所考慮的事件域。根據這樣的直觀想法，利用機率論公理化的語言，取實數值的隨機變數的數學定義可確切地表述如下：機率空間$(\Omega ,F,p)$上的隨機變數$X$是定義於$\Omega$上的實值可測函式，即對任意$\omega \in \Omega$，$X(\omega )$為實數，且對任意實數$x$，使$X(\omega )\leq x$的一切$\omega$組成的$\Omega$的子集$\{\omega :X(\omega )\leq x\}$是事件，也即是$F$中的元素。事件$\{\omega :X(\omega )\leq x\}$常簡記作$\{X\leq x\}$，並稱函式$F(x)=p(X\leq x)$，$-\infty <x<\infty$ ，為$X$的分布函式。 設$X$, $Y$是機率空間$(\Omega ,F,p)$上的兩個隨機變數，如果除去一個零機率事件外，$X(\omega )$與$Y(\omega )$相同，則稱$X=Y$以機率1成立，也記作$p(X=Y)=1$或$X=Y$,α.s.（α.s.意即幾乎必然）。

有些隨機現象需要同時用多個隨機變數來描述。例如對地面目標射擊，彈著點的位置需要兩個坐標才能確定，因此研究它要同時考慮兩個隨機變數，一般稱同一機率空間$(\Omega ,F,p)$上的$n$個隨機變數構成的$n$維向量$X=(x_{1},x_{2},\ldots ,x_{n})$為$n$維隨機向量。隨機變數可以看作一維隨機向量。稱$n$元$x_{1},x_{2},\ldots ,x_{n}$的函式為$X$的（聯合）分布函式。又如果$(x_{1},x_{2})$為二維隨機向量，則稱$x_{1}+ix_{2}(i^{2}=-1)$為復隨機變數。 隨機變數的獨立性 　獨立性是機率論所獨有的一個重要概念。設$x_{1},x_{2},\ldots ,x_{n}$是$n$個隨機變數，如果對任何$n$個實數$x_{1},x_{2},\ldots ,x_{n}$都有 即它們的聯合分布函式$F(x_{1},x_{2},\ldots ,x_{n})$等於它們各自的分布函式$F1(x_{1}),F2(x_{2}),\ldots ,Fn(x_{n})$的乘積。則稱$x_{1},x_{2},\ldots ,x_{n}$是獨立的。這一定義可以直接推廣到每一$xk$（$k=1,2,\ldots ,n$）是隨機向量的情形。獨立性的直觀意義是：$x_{1},x_{2},\ldots ,x_{n}$中的任何一個取值的機率規律，並不隨其中的其他隨機變數取什麼值而改變。在實際問題中通常用它來表徵多個獨立操作的隨機試驗結果或多種有獨立來源的隨機因素的機率特性，因此它對於機率統計的應用是十分重要的。

從隨機變數（或向量）$x_{1},x_{2},\ldots ,x_{n}$的獨立性還可以推出：設$Bk$是$xk$取值的空間中的任意波萊爾集，$k=1,2,\ldots ,n$。設$x_{1},x_{2},\ldots ,x_{n}$是獨立的，則它們中的任意個都是獨立的。但逆之即使其中任何$n-1$個是獨立的，也不保證$x_{1},x_{2},\ldots ,x_{n}$是獨立的。又如果$fj(x),i=1,2,\ldots ,n$，是$n$個連續函式或初等函式(或更一般的波萊爾可測函式)，則從$x_{1},x_{2},\ldots ,x_{n}$的獨立性可推出$f1(x_{1}),f2(x_{2}),\ldots ,fn(x_{n})$也獨立。如果隨機變數(隨機向量)序列$x_{1},x_{2},\ldots ,x_{n},\ldots$中任何有限個都獨立，則稱之為獨立隨機變數（隨機向量）序列。 關於隨機變數的動差、特徵函式、母函式及半不變數，分別見數學期望值、變異數、動差及機率分布。

隨機變數的函式

一個新的隨機變數能被鮑萊耳可測函式定義 $g\colon \mathbb {R} \rightarrow \mathbb {R}$ 來產生一個隨機變數$X$。$Y$的累積分布函式是：

$F_{Y}(y)=\operatorname {P} (g(X)\leq y).$

如果鮑萊耳函式可逆：

$F_{Y}(y)=\operatorname {P} (g(X)\leq y)={\begin{cases}\operatorname {P} (X\leq g^{-1}(y))=F_{X}(g^{-1}(y)),&{\text{if }}g^{-1}{\text{ increasing}},\\\\\operatorname {P} (X\geq g^{-1}(y))=1-F_{X}(g^{-1}(y)),&{\text{if }}g^{-1}{\text{ decreasing}}.\end{cases}}$

得到它的機率密度函式：

$f_{Y}(y)=f_{X}(g^{-1}(y))\left|{\frac {dg^{-1}(y)}{dy}}\right|.$

例子

定義$X$為實數，在連續性隨機變數里，讓 $Y=X^{2}$

$F_{Y}(y)=\operatorname {P} (X^{2}\leq y).$

如果$y<0$，那麼 $P(X^{2}\leq y)=0$

$F_{Y}(y)=0\qquad {\hbox{if}}\quad y<0.$

如果$y\geq 0$

$\operatorname {P} (X^{2}\leq y)=\operatorname {P} (|X|\leq {\sqrt {y}})=\operatorname {P} (-{\sqrt {y}}\leq X\leq {\sqrt {y}}),$

可以得到：

$F_{Y}(y)=F_{X}({\sqrt {y}})-F_{X}(-{\sqrt {y}})\qquad {\hbox{if}}\quad y\geq 0.$

參考文獻

• Fristedt, Bert; Gray, Lawrence. A modern approach to probability theory. Boston: Birkhäuser. 1996 [2017-03-01]. ISBN 3-7643-3807-5. （原始內容存檔於2021-04-28）. 
• Kallenberg, Olav. Random Measures 4th. Berlin: Akademie Verlag. 1986. ISBN 0-12-394960-2. MR 0854102. 
• Kallenberg, Olav. Foundations of Modern Probability 2nd. Berlin: Springer Verlag. 2001 [2017-03-01]. ISBN 0-387-95313-2. （原始內容存檔於2021-04-02）. 
• Papoulis, Athanasios. Probability, Random Variables, and Stochastic Processes 9th. Tokyo: McGraw–Hill. 1965 [2017-03-01]. ISBN 0-07-119981-0. （原始內容存檔於2017-06-26）. 

外部連結

• Hazewinkel, Michiel (編), Random variable, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
• Zukerman, Moshe, Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF), 2014 [2017-03-01], （原始內容 (PDF)存檔於2016-08-11） 
• Zukerman, Moshe, Basic Probability Topics (PDF), 2014 [2017-03-01], （原始內容 (PDF)存檔於2021-04-02） 

參見

• 機率論
• 隨機分布
• 隨機性
• 隨機函式
• 生成函式
• 演算法資訊理論
• 隨機變數的收斂