量子计算机
量子計算機是一种使用量子邏輯實現通用計算的設備。不同於電子計算機，量子計算用來存儲數據的對象是量子比特，它使用量子算法來進行數據操作。一般認為量子計算機仍處於研究階段。 然而2011年5月11日, 加拿大的D-Wave System Inc. 發布了一款號稱 “全球第一款商用型量子计算机”的計算設備“D-Wave One”[1]。 該量子設備是否真的實現了量子計算目前還沒有得到學術界廣泛認同[2]。
目录 |
历史 [编辑]
隨著計算機科學的發展，史蒂芬·威斯納在1969年最早提出“基於量子力學的計算設備”。而关于"基於量子力學的信息處理"的最早文章則是由亞歷山大·豪勒夫（1973）、帕帕拉維斯基（1975）、羅馬·印戈登（1976）和尤里·馬尼（1980）年發表[3][4][5] [6]。史蒂芬·威斯納的文章發表於1983年[7]。1980年代一系列的研究使得量子計算機的理論變得豐富起來。1982年，理查德·費曼在一個著名的演講中提出利用量子體系實現通用計算的想法。緊接著1985年大衛·杜斯提出了量子圖靈機模型 [8]。人們研究量子计算机最初很重要的一個出發點是探索通用計算機的計算極限。當使用計算機模擬量子現象時，因為龐大的希爾伯特空間而資料量也變得龐大。一個完好的模擬所需的運算時間則變得相當可觀，甚至是不切實際的天文數字。理查德·費曼當時就想到如果用量子系統所構成的計算機來模擬量子現象則運算時間可大幅度減少，從而量子計算機的概念誕生。
量子計算機在1980年代多處於理論推導狀態。1994年彼得·秀爾（Peter Shor）提出量子質因數分解演算法後[9]，因其對於現在通行於銀行及網路等處的RSA加密演算法可以破解而構成威脅之後，量子計算機變成了熱門的話題，除了理論之外，也有不少學者著力於利用各種量子系統來實現量子計算機。
半導體靠控制積體電路來記錄及運算資訊，量子電腦則希望控制原子或小分子的狀態，記錄和運算資訊。 1994年，貝爾實驗室的專家彼得·秀爾（Peter Shor）證明量子電腦能做出對數運算[10]，而且速度遠勝傳統電腦。因為量子不像半導體只能記錄0與1，可以同時表示多種狀態。如果把半導體比成單一樂器，量子電腦就像交響樂團，一次運算可以處理多種不同狀況，因此，一個40位元的量子電腦，就能在很短时间内高效解開1024位元電腦花上數十年解決的問題。
量子計算機的基本概念 [编辑]
量子计算机，顾名思义，就是实现量子计算的机器。要说清楚量子计算，首先看傳統计算。傳統计算机从物理上可以被描述为对输入信号序列按一定算法进行变换的机器，其算法由计算机的内部逻辑电路来实现。
- 经典计算机具有如下特点：
- 其输入态和输出态都是傳統信号，用量子力学的语言来描述，也即是:其输入态和输出态都是某一力学量的本征态。如输入二进制序列
，用量子记号，即
。所有的输入态均相互正交。对经典计算机不可能输入如下叠加态：
。 - 傳統计算机内部的每一步变换都演化为正交态，而一般的量子变换没有这个性质，因此，傳統计算机中的变换（或计算）只对应一类特殊集。
，用量子记号，即
。所有的输入态均相互
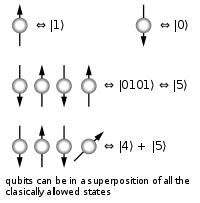
。相应于经典计算机的以上两个限制，量子计算机分别作了推广。量子计算机的输入用一个具有有限能级的量子系统来描述，如二能级系统（称为量子位元（qubits））,量子计算机的变换（即量子计算）包括所有可能的正变换。
- 因此量子计算机的特点为:
- 量子计算机的输入态和输出态为一般的叠加态，其相互之间通常不正交；
- 量子计算机中的变换为所有可能的正变换。得出输出态之后，量子计算机对输出态进行一定的测量，给出计算结果。
由此可见，量子计算对傳統计算作了极大的扩充，傳統计算是一类特殊的量子计算。量子计算最本质的特征为量子叠加性和量子相干性。量子计算机对每一个叠加分量实现的变换相当于一种经典计算，所有这些傳統计算同时完成，并按一定的概率振幅叠加起来，给出量子计算机的输出结果。这种计算称为量子并行计算。
目前發展的系統 [编辑]
包括如下物理系統：
- 液態核磁共振量子電腦（liquid-state NMR quantum computer）
- 固態核磁共振量子電腦（silicon-based NMR quantum computer）
- 離子陷阱（ion trap）
- 量子光學（quantum optics）
- 腔室量子電動力學（cavity QED）
- 超導體方案
- 拓撲量子計算（topological quantum computing）
相關條目 [编辑]
參考 [编辑]
- ^ Quantum annealing with manufactured spins, Nature 473-7346
- ^ Controversial Computer Is at Least a Little Quantum Mechanical, Science, 13 May 2011
- ^ Holevo, A.S. (1973), ‘Bounds for the quantity of information transmitted by a quantum communication channel’, Problemy Peredachi Informatsii, 9(3): 3–11. English translation in Problems of Information Transmission, 9: 177–183, 1973.
- ^ Ingarden, R.S. (1976), ‘Quantum information theory’, Rep. Math. Phys., 10: 43–72.
- ^ Manin, Y. (1980), Computable and Uncomputable, Moscow: Sovetskoye Radio.
- ^ Poplavskii, R.P (1975), ‘Thermodynamical models of information processing’, (in Russian). Uspekhi Fizicheskikh Nauk, 115(3): 465–501.
- ^ Wiesner, S. (1983), ‘Conjugate coding’, Sigact news, 18: 78–88.
- ^ David Deutsch, Quantum theory, the Church-Turingprinciple and the universal quantum computer, Proc. R. Soc. Lond.
- ^ Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM J. Comput. 26 (5): 1484–1509, arXiv:quant-ph/9508027v2
- ^ Peter Shor, Algorithms for Quantum Computation: Discrete Logarithms and Factoring, IEEE Symposium on Foundations of Computer Science 124-134(1994)
外部連結 [编辑]
Loser: D-Wave Does Not Quantum Compute
On quantum physics and computer simulation, R.P.Feynman
|
|||||||||||||||||||||||||||||||||||
