馬克士威方程組

馬克士威方程組(英語:Maxwell's equations),或稱馬克士威-黑維塞方程組(英語:Maxwell-Heaviside equations)[1],是一組描述電場、磁場與電荷密度、電流密度之間關係的偏微分方程式。該方程組由四個方程式組成,分別是描述電荷如何產生電場的高斯定律、表明磁單極子不存在的高斯磁定律、解釋時變磁場如何產生電場的法拉第感應定律,以及說明電流和時變電場怎樣產生磁場的馬克士威-安培定律。馬克士威方程組是因英國物理學家詹姆斯·馬克士威而命名[註 1]。馬克士威在19世紀60年代構想出這方程組的早期形式。[2]
在不同的領域會使用到不同形式的馬克士威方程組。例如,在高能物理學與重力物理學裏,通常會用到時空表述的馬克士威方程組版本。這種表述建立於結合時間與空間在一起的愛因斯坦時空概念,而不是三維空間與第四維時間各自獨立展現的牛頓絕對時空概念。[3]:1ff愛因斯坦的時空表述明顯地符合狹義相對論與廣義相對論。[註 2]在量子力學裏,基於電位與磁勢的馬克士威方程組版本比較獲人們青睞。[4]:33
自從20世紀中期以來,物理學者已明白馬克士威方程組不是精確規律,精確的描述需要藉助更能顯示背後物理基礎的量子電動力學理論,而馬克士威方程組只是它的一種古典場論近似。儘管如此,對於大多數日常生活中涉及的案例,通過馬克士威方程組計算獲得的解答跟精確解答的分歧甚為微小。而對於非古典光、雙光子散射、量子光學與許多其它與光子或虛光子相關的現象,馬克士威方程組不能給出接近實際情況的解答。[4]:1[5]:9-13
從馬克士威方程組,可以推論出光波是電磁波。馬克士威方程組和勞侖茲力方程式是古典電磁學的基礎方程式。得益於這一組基礎方程式以及相關理論,許多現代的電力科技與電子科技得以被發明並快速發展。
概論
[編輯]馬克士威方程組是由四個一階線性偏微分方程式共同組成。[6] :326-333雖然一階與線性都是良好的數學性質,除了具有高度對稱性的案例以外,通常找不到它的解析解,因此必須使用數值方法來找到它的數值解。但由於電動力學是一種線性理論,可以利用疊加原理來求解。[註 3][5]:9-13[7]
高斯定律
[編輯]高斯定律描述電場是怎樣由電荷生成。電場線開始於正電荷,終止於負電荷。從估算穿過某給定閉曲面的電場線數量,即電通量,可以得知包含在這閉曲面內的總電荷。更詳細地說,該定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷數量之間的關係。[8]:190-195

高斯磁定律
[編輯]高斯磁定律表明,磁單極子(磁荷)並不存在於宇宙。在實驗方面,物理學者迄今仍尚未發現磁單極子存在的明確證據。[9]由物質產生的磁場是被一種稱為偶極子的位形所生成。磁偶極子最好是用電流迴路來表示。磁偶極子好似不可分割地被束縛在一起的正磁荷和負磁荷,其淨磁荷為零。磁場線沒有初始點,也沒有終止點。磁場線會形成迴圈或延伸至無窮遠。換句話說,進入任何區域的磁場線,也必須從那區域離開。以術語來說,通過任意閉曲面的磁通量等於零,磁場是一個螺線向量場。[8]:201-203
部分學者[5]:237-238[6]:321認為這個定律沒有名字或稱之為無自由磁單極子定律。
法拉第感應定律
[編輯]法拉第感應定律描述時變磁場怎樣感應出電場。電磁感應是許多發電機的運作原理。例如,一塊旋轉的條形磁鐵會產生時變磁場,這又會生成電場,使得鄰近的閉迴圈因而感應出電流。[10]:134。[6]:294-300
馬克士威-安培定律
[編輯]馬克士威-安培定律闡明,磁場可以用兩種方法生成:一種是靠電流(最初安培定律描述的方法)產生,另一種是靠隨時間變化的電場(馬克士威修正項描述的方法)產生。在電磁學裏,馬克士威修正項意味著時變電場可以生成磁場,而由於法拉第感應定律,時變磁場又可以生成電場。這樣,如果時變電場恰好產生變磁場,則根據這兩個方程式,這種相互產生的電場和磁場(即電磁波)將可以自我持續在空間里傳播(更詳盡內容,請參閱條目電磁波方程式)。[8]:199-201
方程組彙覽
[編輯]這裏展示出馬克士威方程組的兩種等價表述:微觀表述與宏觀表述。
微觀表述專門計算在真空中原子尺度的有限源電荷與有限源電流所產生的電場與磁場。物質可以視為由點電子與點原子核所組成,而內部其它大部分空間都是真空。但是,由於電子與原子核的數量很大,實際而言,無法一一納入計算。事實上,古典電磁學也不需要過度精確的答案。使用微觀馬克士威方程組有兩個主要目的,一是推導出宏觀馬克士威方程組,二是從原子性質估算出宏觀物質參數,例如電容率、磁導率等等。微觀表述可以給出很多宏觀表述所無法給出的極具價值的資訊。[11]:1-2
宏觀表述不將物質內部的原子結構納入考量,而是將物質視為一種連續性介質,其性質決定於電容率、磁導率等等宏觀物質參數。從做實驗可以獲得宏觀物質參數與物質的本質、密度、溫度等等的關係。宏觀馬克士威方程組可以用來預測帶電粒子、電場與磁場的平均性質。採用這種表述會使得在介電質或磁化物質內各種物理計算更加簡易。[5]:248-249[11]:1-2
採用不同的單位制,馬克士威方程組的形式會稍微有所改變,大致形式仍舊相同,只是不同的常數會出現在方程式內部不同位置。國際單位制(SI)是最常使用的單位制,在工程學、化學領域大多都採用這種單位制,大學物理教科書也幾乎都使用這種單位制。其它常用的單位制有高斯單位制、勞侖茲-黑維塞單位制和普朗克單位制。由公分-克-秒制衍生的高斯單位制,比較適合於教學用途,能夠使得方程式看起來更簡單、更易懂。[12][13]稍後會詳細闡述高斯單位制。勞侖茲-黑維塞單位制也是衍生於公分-克-秒制,主要用於粒子物理學。[14]:9普朗克單位制是一種自然單位制,其單位都是根據大自然的性質定義,不是由人為設定。普朗克單位制是研究理論物理學非常有用的工具,能夠在理論論述裏給出很大的啟示。[5]:775[15]
在本條目中,除非特別指出,所有方程式都採用國際單位制。
在真空裏的馬克士威方程組
[編輯]| 名稱 | 微分形式 | 積分形式 |
|---|---|---|
| 高斯定律 | ||
| 高斯磁定律 | ||
| 法拉第電磁感應定律 | ||
| 馬克士威-安培定律 |
這種形式的馬克士威方程組又稱為「微觀馬克士威方程組」,可以用來推導出宏觀馬克士威方程組,也可以用來找出原子性質與宏觀性質兩者之間的關聯。[11]:1, 4[5]:2, 248
有介電質時的馬克士威方程組
[編輯]| 名稱 | 微分形式 | 積分形式 |
|---|---|---|
| 高斯定律 | ||
| 高斯磁定律 | ||
| 法拉第電磁感應定律 | ||
| 馬克士威-安培定律 |
這種形式的馬克士威方程組又稱為「宏觀馬克士威方程組」,特別適用於描述在介電質中的電磁性質,稍後會有更詳細論述。[11]:1[5]:2, 248
馬克士威方程組術語符號表格
[編輯]以下表格給出每一個符號所代表的物理意義,和其單位:
| 符號 | 物理意義 | 國際單位[5]:782-783 |
|---|---|---|
| 電場強度 | 伏特/公尺、牛頓/庫侖 | |
| 磁通量密度 | 特士拉、韋伯/公尺2、伏特·秒/公尺2 | |
| 電位移 | 庫侖/公尺2、牛頓/伏特·公尺 | |
| 磁場強度 | 安培/公尺 | |
| 散度算符 | /公尺 | |
| 旋度算符 | ||
| 對於時間的偏導數 | /秒 | |
| 曲面積分的運算曲面 | 公尺2 | |
| 路徑積分的運算路徑 | 公尺 | |
| 微小面元素向量 | 公尺2 | |
| 微小線元素向量 | 公尺 | |
| 電常數 | 法拉/公尺 | |
| 磁常數 | 亨利/公尺、牛頓/安培2 | |
| 自由電荷密度 | 庫侖/公尺3 | |
| 總電荷密度 | 庫侖/公尺3 | |
| 在閉曲面裏面的自由電荷 | 庫侖 | |
| 在閉曲面裏面的總電荷 | 庫侖 | |
| 自由電流密度 | 安培/公尺2 | |
| 總電流密度 | 安培/公尺2 | |
| 穿過閉路徑所包圍的曲面的自由電流 | 安培 | |
| 穿過閉路徑所包圍的曲面的總電流 | 安培 | |
| 穿過閉路徑所包圍的曲面的磁通量 | 特士拉·公尺2、伏特·秒,韋伯 | |
| 穿過閉路徑所包圍的曲面的電通量 | 焦耳·公尺/庫侖 | |
| 穿過閉路徑所包圍的曲面的電位移通量 | 庫侖 |
微觀尺度與宏觀尺度
[編輯]在古典電磁學裏,微觀尺度指的是系統尺寸的數量級大於10−14公尺的尺度範圍。滿足微觀尺度,電子和原子核可以視為點電荷,微觀馬克士威方程組成立;否則,必需將原子核內部的電荷分佈納入考量。在微觀尺度計算出來的電場與磁場仍舊變化相當劇烈,空間變化的距離數量級小於10−10公尺,時間變化的週期數量級在10−17至10−13秒之間。因此,從微觀馬克士威方程組,必需經過古典平均運算,才能得到平滑、連續、緩慢變化的宏觀電場與宏觀磁場。宏觀尺度的最低極限為10−8公尺。這意味著電磁波的反射與折射行為可以用宏觀馬克士威方程組來描述。以這最低極限為邊長,體積為10−24立方公尺的立方體大約含有106個原子核和電子。這麼多原子核和電子的物理行為,經過古典平均運算,足以平緩任何劇烈的漲落。根據可靠文獻記載,古典平均運算只需要在空間作平均運算,不需要在時間作平均運算,也不需要考慮到原子的量子效應。[5]:248-249
古典平均運算是一種比較簡單的平均程序,給定函數,這函數的空間平均定義為
- ;
其中,是平均運算的空間,是權重函數。
很多函數都可以選為優良的權重函數,高斯函數正是一例:
- 。
最早出現的馬克士威方程式和其相關理論是為宏觀物質設計的,是一種現象學。在那時候,物理學者並不清楚造成電磁現象的基本原因。後來,按照物質的粒子繪景,才推導出微觀馬克士威方程式。二十世紀前半期,在量子力學、相對論、與粒子物理學領域的突破與發展,其嶄新理論與微觀馬克士威方程組相結合,成為建立量子電動力學的關鍵基石。這是物理學中最準確的理論,所計算出的結果能夠精確地符合實驗數據[16]:1-2。
數學性質
[編輯]馬克士威方程組形似超定組:它只涉及到六個未知量(向量電場、磁場各擁有三個未知量,電流與電荷不是未知量,而是自由設定並符合電荷守恆的物理量),但卻是由八個方程式所組成(兩個高斯定律共有兩個方程式,法拉第定律與馬克士威-安培定律各有三個方程式)。經過仔細分析,即可明白,實際上並不是這麼簡單。
馬克士威方程組的方程式具有「獨立性」──從方程組內的任何一個或多個方程式,都不能推導出方程組內的任何其它方程式。這意味著馬克士威方程組不是超定組,其內中沒有重複任何功能的方程式。馬克士威方程組、洛侖茲力方程式與牛頓第二運動定律總合起來具有「完備性」,他們可以說明所有古典電動力學的現象,不需要使用到任何其它方程式。在某區域內,給定適當的初始條件與邊界條件,則馬克士威方程組的解答具有「唯一性」,即每一個應變量只能有一種函數形式,其內部只含有常數或自變量,不含有任何其它應變量。[17][5]:239
法拉第定律與馬克士威-安培定律共同主導著在空間內電磁場隨著時間流易的演化,而高斯定律與高斯磁定律則是約束方程式,電磁場必須在所有時間與空間遵守這兩個約束方程式。理論而言,可以假設某種電磁場在所有空間服從法拉第定律與馬克士威-安培定律的指揮,反之,如果他們不遵守高斯定律與高斯磁定律的約束,則它們無法實際存在於真實世界。換句話說,法拉第定律與馬克士威-安培定律會給出額外的解答,其不符合高斯定律與高斯磁定律的約束。[18][19]:1019-1020
舉例而言,假設電荷源與電流源為零,採用直角坐標系,根據高斯定律與高斯磁定律,對於電場與磁場在空間每一個位置可以分別自由設定兩個分量,、與、(需要給出4個函數),由於
- 、
- ,
只要在任意一個xy-平面的每一個位置分別設定與(需要給出2個函數),則可估算在空間每一個其它位置的與。知道這些與的資訊,則可使用法拉第定律與馬克士威-安培定律估算出在所有時間與的資訊。
證明兩種形式等價
[編輯]前面所表述的馬克士威方程組的兩種形式,在數學上等價。
兩種高斯定律數學等價的證明 本段落證明高斯定律對於總電荷的方程式[6]:326-330 - ,
等價於高斯定律對於自由電荷的方程式
- 。
請注意,這裏只處理微分形式,不處理積分形式。這已達成足夠條件。因為,根據散度定理,兩種高斯定律的方程式,其微分形式都分別等價於積分形式。
電位移的定義式為
- ;
其中,是電極化強度。
束縛電荷密度的定義式為(請參閱電極化)
- 。
注意到是總電荷密度:
- 。
稍加編排,
- 。
所以,若且唯若。兩個方程式等價。
兩種馬克士威-安培定律數學等價的證明 本段落證明馬克士威-安培定律對於總電流的方程式[6]:326-330 - ,
等價於馬克士威-安培定律對於自由電流的方程式
- 。
請注意,這裏只處理微分形式,不處理積分形式。這已達成足夠條件,因為,根據斯托克斯定理,對於這兩種馬克士威-安培定律的方程式,微分形式都分別等價於積分形式。
束縛電流密度的定義式為(請參閱磁化強度)
- ;
其中,是磁化強度。
假設總電流密度是
- 。
根據電荷守恆定律,
- 、
- 。
那麼,
- 。
假若束縛電荷密度含時間,則電荷守恆定律無法被滿足。為了要滿足這定律,總電流密度必須加入一個項目,「極化電流密度」,定義為:
- 。
那麼,
- 。
因此,總電流密度是
- 。
H場定義為
- 。
稍加編排,
- 。
所以,若且唯若。兩個方程式等價。
描述在自由空間裏的電磁波
[編輯]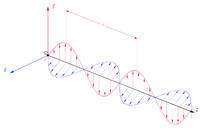
在自由空間裏,不需要考慮到介電質或磁化物質。假設源電流和源電荷為零,則馬克士威方程組寫為[註 4][8]:209-213
- 、
- 、
- 、
- 。
從這方程組,應用一些向量恆等式,經過一番簡單的運算,可以得到電場與磁場的波動方程式:
- 、
- 。
對於這兩個波動方程式,平面行進正弦波是個解答波,其電場和磁場相互垂直,並且分別垂直於行進的方向,因此是個橫波。電場與磁場同相位地以光速 傳播:[註 5]
- 。
仔細地觀察馬克士威方程組,就可以發現這方程組很明確地解釋了電磁波怎樣傳播於空間。根據法拉第感應定律,時變磁場會生成電場;根據馬克士威-安培定律,時變電場又生成了磁場。這不停的循環使得電磁波能夠以光速傳播於空間。
1856年,威廉·韋伯和魯道夫·科爾勞施作萊頓瓶實驗,從實驗數據計算出 的數值,他們發現,這數值非常接近於先前從天文學得到的光波傳播於行星際空間的速度。[21]:259-260從這實驗結果,馬克士威正確地斷定光波就是一種電磁輻射。[21]:283
描述在物質裏的電磁性質
[編輯]束縛電荷和束縛電流
[編輯]
假設,施加外電場於介電質。施加這個電場的結果是,介電質的分子會形成一個微觀的電偶極子,其伴隨著電偶極矩。分子的原子核會朝著電場的方向稍微遷移位置,而電子則會朝著相反方向稍微遷移位置。這形成了介電質的電極化。如右圖的理想狀況所示,雖然,所有涉及的電荷都仍舊束縛於其原本的分子,由於這些微小遷移所造成的電荷分佈,變得好像是在介電質的一邊形成了一薄層正表面電荷,在另一邊又形成了一薄層負表面電荷。電極化強度定義為介電質內部的電偶極矩密度,也就是單位體積的電偶極矩。在介電質內部,假設電極化強度是均勻的,則宏觀的面束縛電荷只會出現於介電質表面,即進入或離開介電質之處;否則,假設是不均勻的,則介電質內部也會出現束縛電荷。[6]:166-175
與靜電學有些類似的是,在靜磁學裏,假設施加外磁場於物質,響應這動作,物質會被磁化,原子成分會顯示出磁矩。在本質上,這磁矩與原子的各個次原子粒子的角動量有關。其中,響應最顯著的是電子。這角動量的連結,不禁令人聯想到一副圖畫,在圖畫中,磁化物質變成了一群微觀的束縛電流迴路。雖然每一個電荷只是移動於其原子的微觀迴路,一群微觀的束縛電流迴路聚集在一起會形成宏觀的束縛電流循環流動於物質的表面。這些束縛電流可以用磁化強度來描述。磁化強度定義為磁偶極矩在一個磁化物質內的密度,也就是單位體積的磁偶極矩。[6]:262-268
這些非常複雜與粗糙的束縛電荷與束縛電流的物理行為,在宏觀尺度,可以分別以電極化強度與磁化強度來表達。電極化強度與磁化強度分別將這些束縛電荷與束縛電流以恰當的尺度做空間平均,這樣,可以除去單獨整體原子形成的凹凸粗糙結構,但又能夠顯示出強度隨著位置而變化的物理性質。由於所有涉及的向量場都已做過恰當體積的空間平均,宏觀馬克士威方程組忽略了微觀尺度的許多細節。不過,對於了解物質的宏觀尺度性質,這些細節可能不具甚麼重要性。[5]:14
本構關係
[編輯]為了要應用宏觀馬克士威方程組,必須分別找到場與場之間、場與場之間的關係。這些稱為本構關係的物理性質,設定了束縛電荷和束縛電流對於外場的響應。它們實際地對應於物質響應外場作用而產生的電極化或磁化。[22]:44-45
本構關係式的基礎建立於附屬場與的定義式:[8]:413-414
- 、
- ;
其中,是電極化強度,是磁化強度。
電極化強度與磁化強度都是源自於物質對於外電場與外磁場的響應。電極化強度是電場的函數,磁化強度是磁場的函數。因此,本構關係式的一般形式為[5]:14
- 、
- 。
在這裏,使用方括號,而不是圓括號,這樣標記主要是在提醒讀者,函數與參數彼此之間的關係並不簡單,很可能相當複雜,可能與過去歷史有關,也可能是非線性相關。大多數實際物質的本構關係式的獲得都需要使用近似手段,通常是從做實驗找到結果。
在自由空間(即理想真空)裏,不需考慮介電質和磁化物質,本構關係式變得很簡單:[5]:2
- 、
- 。
將這些本構關係式代入宏觀馬克士威方程組,則得到的方程組很像微觀馬克士威方程組,當然,在得到的高斯定律方程式和馬克士威-安培方程式內,總電荷密度和總電流密度分別被自由電荷密度和自由電流密度替代。這符合期待的結果,因為,在自由空間裏,沒有束縛電荷、束縛電流和極化電流。
- 、
- ;
儘管只是線性案例,仍舊可能很複雜。[5]:14-16
- 在均質材料裏,與為常數;在非均質材料裏,則依位置而變換。[23]:463
- 在各向同性材料裏,與為標量;在各向異性材料裏,例如晶體,它們是張量。[23]:463[22]:421
- 對於色散材料,和都跟入射電磁波的頻率有關。[23]:397[22]:625
邊界條件
[編輯]如同其它微分方程組一般,必須設定邊界條件[24]:1ff[25]:261 ff與初始條件[26]:17ff,才能給出馬克士威方程組的唯一解答。
在古典電磁學裏,在一個不含有任何自由電荷和自由電流的區域內的電磁場,必定是來自於其它區域。當解析這狀況時,通過適當的邊界條件或初始條件,可以將區域外的電磁場與這區域的電磁場連結在一起。舉一個電磁波散射的例子,一個來自於散射區域之外的電磁波,遭遇到散射區域內的一個靶子,被這靶子散射出去。在這散射過程裏,由於電磁波與靶子之間交互作用,散射的電磁波含有很多與這靶子性質相關的資訊。經過仔細地分析,將這些資訊萃取出來,就可以更詳細地了解這靶子的性質[27]:45ff。
對於某些案例,譬如波導或空腔共振器,因為像金屬牆壁一類的隔離設施,解答區域大部份孤立於外部世界。在金屬牆壁位置的邊界條件決定了解答區域的電磁場。在解答區域以外的外部世界,只能靠著邊界條件來影響內部的狀況[28]。對於另外一些案例,像光導纖維或薄膜,解答區域時常會被分割為幾個亞區域,每個亞區域都有其簡單獨自的性質。通過亞區域與亞區域之間界面的邊界條件,可以將每一個亞區域的解答連結起來[29]。
應用邊界條件,有時也可以簡化問題,使得問題更容易被了解。例如,均勻物體的電極化可以被更換為在這物體外表的一層面電荷分佈,[6]:166-175或者,均勻物體的磁化被更換為在這物體外表的一層面電流分佈。[6]:263-265詳盡細節,請參閱束縛電荷和束縛電流段落。
高斯單位制
[編輯]公分-克-秒單位制的三個基本單位是長度單位公分、質量單位克、時間單位秒。在古典力學裏,公分-克-秒單位制的單位是一致的;但在電磁學裏,卻出現了幾種變型。高斯單位制是其中一種變形。採用高斯單位制,馬克士威方程組的形式為[12][30]:11, 42
進階表述
[編輯]平直時空裏的協變形式
[編輯]馬克士威方程組與狹義相對論之間的關係密切。不只是因為馬克士威方程組對於狹義相對論的初始發展,做了相當大的貢獻,也因為狹義相對論激盪出一種更簡潔的表述,能以協變張量來表達馬克士威方程組。
自由空間的馬克士威方程組的形式,對於任意慣性坐標系,都是一樣的。在狹義相對論裏,為了要更明確地表達出這論點,必須以四維向量和張量寫出協變形式的馬克士威方程組。這表述的一個構成要素為電磁張量,其是結合了電場和磁場在一起的二階反對稱張量。電磁張量表示為:[6]:535-537
- 。
使用閔考斯基度規,
- ,
將下標拉高為上標,可以得到反變張量:
- 。
的二階對偶張量是
- 。
- ;
其中,是電荷密度,是電流密度。
藉著這些要素,採用愛因斯坦求和約定,馬克士威方程組可以寫為
- 、
- ;
這兩個張量方程式等價於馬克士威方程組。第一個張量方程式表達兩個非齊次馬克士威方程式,高斯定律和馬克士威-安培定律。第二個張量方程式表達兩個齊次馬克士威方程式,高斯磁定律和法拉第感應定律。
勢場表述
[編輯]在高等古典力學裏,電位與磁矢勢可以較為便利地表達與分析電磁理論。這種表述稱為「勢場表述」。在量子力學層次,電動力學幾乎完全使用勢場表述。[4]:33電場與磁場分別以電位與磁矢勢表示為[4]:35-37
- 、
- 。
從這兩個定義式,兩個齊次馬克士威方程式自動成立,另外兩個非齊次方程式變為
- 、
- 。
這兩個勢場方程式組合起來,具有與原本馬克士威方程組同樣的功能和完備性。由於電場和磁場各有三個分量,原本的馬克士威方程組需要解析六個分量。勢場表述只需要解析四個分量,因為電位只有一個分量,磁矢勢有三個分量。可是,勢場表述涉及了二次微分,方程式也比較冗長。
許多不同的與數值組可以得到同樣的電場與磁場。因此,這些數值組相互物理等價,可以自由選擇。這性質稱為規範自由。恰當的選擇可以簡化方程式的形式,或者,可以專門適用於某特別狀況。採用勞侖次規範
- ,
勢場的兩個向量方程式可以寫為兩個具有勞侖茲不變性的方程式:
- 、
- 。
利用達朗白算符來表示將會更簡潔,
- 、
- 。
其中,是達朗白算符,又稱為「四維拉普拉斯算符」。
由磁矢勢和電位共同組成的四維勢以方程式定義為
- 。
二十世紀初,阿諾·索末菲提出了四維向量方程式,這是波恩哈德·黎曼先前想出的一個方程式的推廣,因此,這個方程式被命名為「黎曼-索莫菲方程式」,[31]:37-38或馬克士威方程組的勢場表述的協變形式:[32]:102
- 。
彎曲時空裏的協變形式
[編輯]物質和能量會造成時空彎曲。這是廣義相對論的主題。時空彎曲會影響電動力學的物理。一個電磁場所擁有的能量和動量也會造成時空彎曲。將平直時空的方程組中的偏導數改換為協變導數,就可以得到彎曲時空中的馬克士威方程組:[33]:247
- 、
- ;
其中,是二階電磁張量。
- ;
其中,是表現時空彎曲的克里斯托費爾符號。
所以,馬克士威方程組又可以表示為
- 、
- 。
馬克士威方程組的局限
[編輯]
雖然馬克士威方程組能夠非常成功地解釋與預測各種各樣電磁現象,它對於真實物理給出的是一個近似描述,對於某些特別案例,它所估算出的結果可能會不夠準確。例如,在極強勁場狀況下產生的雙光子散射(電場極值約為1020 V/m,位於古典電子表面的電場)、在兩個電荷之間相隔極短距離所產生的真空極化現象(距離約為電子康普頓波長3.86×10-13 m)。馬克士威方程組無法對於很多現象給出正確解釋,例如,非古典光、電磁場的量子糾纏等等。由於馬克士威方程組完全不能表達光子的概念,任何涉及到單獨光子的現象,例如光電效應、普朗克定律、單光子探測器等等,假若使用馬克士威方程組來解釋,都會遇到困難。對於這些案例,必須用量子電動力學的理論來給予解釋。[5]:9-13
磁單極子
[編輯]| 名稱 | 磁單極子表述 |
|---|---|
| 高斯定律 | |
| 高斯磁定律 | |
| 法拉第感應定律 | |
| 馬克士威-安培定律 |
馬克士威方程組明白顯示出,在宇宙裏,磁荷不存在,只有電荷存在。至今為止,確實從未有任何實驗發現磁荷的存在。假若磁荷存在,則高斯磁定律與法拉第感應定律都需要修改,馬克士威方程組內會增添兩個新的變量,磁荷和磁流。經過修正後的方程組,會對於以下對調運作,具有不變性:[30]:18[4]:20, 70
- 。
這種對調運作是一種廣義對偶變換的一個特別案例。
近期,物理學者發現,有些凝聚體,例如自旋冰,會展示出貌似磁單極子的湧現行為。儘管這些事件被描述為發現盼望已久的磁單極子,它們只是模擬真正的磁單極子。真正的磁單極子必須滿足方程式∇ ⋅ B ≠ 0。在凝聚體系統裏,滿足的是方程式∇ ⋅ B = 0與∇ ⋅ H ≠ 0。[34]
參閱
[編輯]|
|
註釋
[編輯]- ^ 馬克士威在中國大陸被翻譯為「麥克斯韋」,故該方程組也稱「麥克斯韋方程組」。
- ^ 任何形式的馬克士威方程組都符合相對論,但是,時空表述能夠更為顯而易見地滿足符合性。
- ^ 電動力學是線性理論。假設源電荷與源電流為(、)、(、)的兩個電系統,其解答分別為(、……、)與(、……、),則按照疊加原理,源電荷與源電流為(、)的電系統,其解答為(、……、)。
- ^ 術語「真空」時常用來指稱自由空間。但是,在這裏,自由空間指的是一種理想的,實際不可能體現的參考狀態,迥然不同於任何可以實際體現的真空,像實驗室內製造的超高真空或外太空,或任何從理論方面體現的真空,像量子真空或量子色動力真空。
- ^ 國際標準化組織建議使用為自由空間光速的國際標準標記(ISO 31-5)。[20]
參考文獻
[編輯]- ^ Chew, W.C.; Tong, M.S.; Hu, B. Introduction to Computational Electromagnetics. Integral Equation Methods for Electromagnetic and Elastic Waves. 2009: 2. doi:10.1007/978-3-031-01707-0_1.
- ^ Maxwell, J. C., A dynamical theory of the electromagnetic field (pdf), Philosophical Transactions of the Royal Society of London, 1865, 155: 第459–512頁 [2016-10-02], (原始內容存檔 (PDF)於2021-01-17) (頁面存檔備份,存於網際網路檔案館)
- ^ Rafael Ferraro. Einstein's Space-Time: An Introduction to Special and General Relativity. Springer Science & Business Media. 23 September 2007. ISBN 978-0-387-69947-9.
- ^ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Thidé, Bo. Electromagnetic Field Theory 2nd. Dover Publications. 2011. ISBN 978-0486477732. (原始內容存檔於2015-12-02). (頁面存檔備份,存於網際網路檔案館)
- ^ 5.00 5.01 5.02 5.03 5.04 5.05 5.06 5.07 5.08 5.09 5.10 5.11 5.12 5.13 5.14 5.15 5.16 Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc., 1999, ISBN 978-0-471-30932-1
- ^ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 Griffiths, David J., Introduction to Electrodynamics 第三版, Prentice Hall, 1998, ISBN 0-13-805326-X
- ^ IEEEGHN: Maxwell's Equations. Ieeeghn.org. [2008-10-19]. (原始內容存檔於2014-09-16). (頁面存檔備份,存於網際網路檔案館)
- ^ 8.0 8.1 8.2 8.3 8.4 Bekefi, George; Barrett, Alan, Electromagnetic Vibrations, Waves, and Radiation, USA: MIT Press, 1977, ISBN 0-262-52047-8
- ^ Jackson, John. Maxwell's equations. Science Video Glossary. Berkeley Lab. [2016-07-23]. (原始內容存檔於2019-01-29). (頁面存檔備份,存於網際網路檔案館)
- ^ Crowell, B. Electricity and Magnetism. Light and Matter. 2000. ISBN 0-9704670-4-4.
- ^ 11.0 11.1 11.2 11.3 Kimball Milton; J. Schwinger. Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer Science & Business Media. 18 June 2006. ISBN 978-3-540-29306-4.
- ^ 12.0 12.1 Littlejohn, Robert. Gaussian, SI and Other Systems of Units in Electromagnetic Theory (pdf). Physics 221A, University of California, Berkeley lecture notes. Fall 2007 [2008-05-06]. (原始內容存檔 (PDF)於2012-07-11). (頁面存檔備份,存於網際網路檔案館)
- ^ Silsbee, Francis. Systems of Electrical Units (PDF). JOURNAL OF RESEARCH of the Nationol Bureau of Standards- C. Engineering and Instrumentation. April–June 1962, 66C (2): 第137–183頁 [2016-06-18]. doi:10.6028/jres.066C.014. (原始內容存檔 (PDF)於2021-04-05). (頁面存檔備份,存於網際網路檔案館)
- ^ Griffiths, David J., Introduction to Elementary Particles 第二版, Wiley-VCH Verlag Gmbh & Co., 2008, ISBN 978-3-527-40601-2
- ^ Wilczek, Frank, Scaling Mount Planck I: A View from the Bottom, Physics Today, June 2001, 54 (6): 第12頁 [2018-05-12], (原始內容存檔於2021-04-05) (頁面存檔備份,存於網際網路檔案館)
- ^ Cho, Kikuo. Reconstruction of Macroscopic Maxwell Equations: A Single Susceptibility TheoryVolume 237 of Springer Tracts in Modern Physics illustrated. Springer. 2010. ISBN 978-3-642-12790-8. doi:10.1007/978-3-642-12791-5.
- ^ Zhou, X. L. ON INDEPENDENCE, COMPLETENESS OF MAXWELL’S EQUATIONS AND UNIQUENESS THEOREMS IN ELECTROMAGNETICS. Progress In Electromagnetics Research. 2006, 64: 第117–134頁 [2017-08-07]. doi:10.2528/PIER06061302. (原始內容存檔於2017-08-07). (頁面存檔備份,存於網際網路檔案館)
- ^ J Rosen. Redundancy and superfluity for electromagnetic fields and potentials. American Journal of Physics: 第1071頁. Bibcode:1980AmJPh..48.1071R. doi:10.1119/1.12289.
- ^ Albert Messiah. Quantum Mechanics. Courier Corporation. 17 February 2014. ISBN 978-0-486-79166-1.
- ^ Taylor, Barry; Thomson, Ambler (編). The International System of Units (SI) (PDF). NIST. 2008 [2016-07-23]. (原始內容存檔 (PDF)於2018-12-25). (頁面存檔備份,存於網際網路檔案館)
- ^ 21.0 21.1 Whittaker, E. T., A history of the theories of aether and electricity. Vol 1, Nelson, London, 1951
- ^ 22.0 22.1 22.2 22.3 Andrew Zangwill. Modern Electrodynamics. Cambridge University Press. 2013. ISBN 978-0-521-89697-9.
- ^ 23.0 23.1 23.2 Kittel, Charles, Introduction to Solid State Physics 8th, USA: John Wiley & Sons, Inc., 2005, ISBN 978-0-471-41526-8
- ^ Peter Monk. Finite Element Methods for Maxwell's Equations. Oxford UK: Oxford University Press. 2003. ISBN 0-19-850888-3.
- ^ Thomas B. A. Senior & John Leonidas Volakis, Approximate Boundary Conditions in Electromagnetics, London UK: Institution of Electrical Engineers, 1995, ISBN 0852968493
- ^ Henning F. Harmuth & Malek G. M. Hussain, Propagation of Electromagnetic Signals, Singapore: World Scientific, 1994, ISBN 9810216890
- ^ Khosrow Chadan; et al, An introduction to inverse scattering and inverse spectral problems, Society for Industrial and Applied Mathematics, 1997, ISBN 0898713870
- ^ S. F. Mahmoud, Chapter 2, Electromagnetic Waveguides: Theory and Applications applications, London UK: Institution of Electrical Engineers, 1991, ISBN 0863412327
- ^ Korada Umashankar, Introduction to Engineering Electromagnetic Fields, Singapore: World Scientific: 359ff, 1989, ISBN 9971509210
- ^ 30.0 30.1 Julian Schwinger; Lester L Jr Deraad; K. A. Milton. Classical Electrodynamics. Westview Press. 11 September 1998. ISBN 978-0-8133-4662-5.
- ^ Carver A. Mead. Collective Electrodynamics: Quantum Foundations of Electromagnetism. MIT Press. 2000. ISBN 9780262632607.
- ^ Frederic V. Hartemann. High-field electrodynamics. CRC Press. 2002. ISBN 9780849323782.
- ^ 33.0 33.1 Eric Poisson; Clifford M. Will. Gravity: Newtonian, Post-Newtonian, Relativistic. Cambridge University Press. 29 May 2014. ISBN 978-1-107-03286-6.
- ^ D. J. P. Morris, etc., Dirac Strings and Magnetic Monopoles in the Spin Ice Dy2Ti2O7, Science, 16 October 2009, 326 (5951): 第411–414頁 [2010-01-17], doi:10.1126/science.1178868, (原始內容存檔於2009-11-09) (頁面存檔備份,存於網際網路檔案館)























































































![{\displaystyle \mathbf {D} =\mathbf {D} [\mathbf {E} ,\mathbf {B} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae56f242b988bfb61989e6bdaeabfe2e704d8380)
![{\displaystyle \mathbf {H} =\mathbf {H} [\mathbf {E} ,\mathbf {B} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c855c5c2f1e40e366765745db2df7da3701f3033)


































































