勾股定理

直角邊的平方和等於斜邊的平方

几何学
一个球面投射到一个平面。
纲要 历史
分支 欧几里得 非欧几里得 椭圆 球面 双曲 射影 仿射 合成 解析 代数 微分 黎曼 辛几何 有限
概念 特性 维度 尺规作图 角度 曲线 对角线 平行 垂直 顶点 全等 相似 对称
零 / 一维 点 直线 线段 射线 长度
二维 平面 面积 多边形 三角形 Altitude 斜边 邊長 勾股定理 平行四边形 正方形 三角形 菱形 平行四边形 四边形 梯形 等腰梯形 筝形 圆形 直径 周长 面积
三维 空間 多面體 体积 表面積 正多面體 凸正多面體 六面體 立方體 長方體 四角柱 平行六面體 幾何體 棱锥 圆锥体 棱柱 圆柱体 球體 直径 體積與表面積 球缺
四维- / 其他维度 多胞形 四维凸正多胞体 四維超正方體 超球體
几何学家
按照姓名 会田安明 阿耶波多 Ahmes 海什木 阿波罗尼奥斯 阿基米德 阿蒂亚 Baudhayana 鲍耶 Brahmagupta Cartan Descartes 欧几里得 欧拉 高斯 格罗莫夫 希尔伯特 Jyeṣṭhadeva Kātyāyana Khayyám 克莱因 罗巴切夫斯基 Manava 闵可夫斯基 明安图 帕斯卡 毕达哥拉斯 Parameshvara 庞加莱 黎曼 Sakabe Sijzi 图西 維布倫 Virasena 杨辉 al-Yasamin 张衡 几何学家列表
按照时期 公元前 Ahmes Baudhayana Manava 毕达哥拉斯 欧几里得 阿基米德 阿波罗尼奥斯 1–1400年代 张衡 Kātyāyana 阿耶波多 Brahmagupta Virasena 海什木 Sijzi Khayyám al-Yasamin al-Tusi 杨辉 Parameshvara 1400–1700年代 Jyeṣṭhadeva Descartes 帕斯卡 明安图 欧拉 Sakabe 会田安明 1700–1900年代 高斯 罗巴切夫斯基 鲍耶 黎曼 克莱因 庞加莱 希尔伯特 闵可夫斯基 Cartan 維布倫 现代 阿蒂亚 格罗莫夫
几何学主题

勾股定理，又稱畢達哥拉斯定理（Pythagoras theorem）、勾股定理、畢氏定理、商高定理、新娘座椅定理、百牛定理，是平面几何中一个基本而重要的定理。勾股定理说明，平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方。反之，若平面上三角形中两边长的平方和等于第三边边长的平方，则它是直角三角形（直角所对的边是第三边）。勾股定理是人类早期发现并证明的重要数学定理之一。

《周髀算經》记述公元前一千多年，商高以$(3,4,5)$這組勾股數为例解释了勾股定理要素，论证「弦长平方必定是两直角边的平方和」，确立了直角三角形两条直角边的平方和等于斜边平方的判定原则。其判定方法因后世不明其法而被忽略。

古埃及在公元前2600年的纸莎草記載有$(3,4,5)$这一组勾股数，而古巴比伦泥板紀錄的最大的一个勾股数组是$(12709,13500,18541)$。

有些參考資料提到法国和比利時將勾股定理称为驴桥定理，但驴桥定理是指等腰三角形的二底角相等，非勾股定理。

畢氏定理有四百多個證明，如微分證明，面積證明等。

定理

在平面上的一個直角三角形中，两个直角边边长的平方加起来等于斜邊长的平方。如果设直角三角形的两条直角边长度分别是$a$和$b$，斜边长度是$c$，那么可以用数学语言表达：

$a^{2}+b^{2}=c^{2}$

餘弦定理是勾股定理的一個推广。勾股定理現約有400種證明方法，是數學定理中證明方法最多的定理之一。

其他形式

如果$c$是斜邊的長度而a和b是另外兩條邊的長度，勾股定理可以寫成：

$a^{2}+b^{2}=c^{2}\,$

如果$a$和$b$知道，$c$可以這樣寫：

$c={\sqrt {a^{2}+b^{2}}}.\,$

如果斜邊的長度$c$和其中一條邊（$a$或$b$）知道，那另一邊的長度可以這樣計算：

$a={\sqrt {c^{2}-b^{2}}}.\,$

或

$b={\sqrt {c^{2}-a^{2}}}.\,$

簡單來說，只要知道直角三角形的其中兩條邊長，便能求出第三條邊長。

勾股数组

主条目：勾股数

勾股数组是滿足勾股定理$a^{2}+b^{2}=c^{2}$的正整數組$(a,b,c)$，其中的$a,b,c$称为勾股数。例如$(3,4,5)$就是一組勾股数組。

任意一组勾股数$(a,b,c)$可以表示为如下形式：$a=k(m^{2}-n^{2}),b=2kmn,c=k(m^{2}+n^{2})$，其中$k,m,n\in \mathbb {N*} ,m>n$。

歷史

公元前18世纪记录各种勾股数组的巴比伦石板

這個定理的歷史可以被分成三個部份：發現勾股数、發現直角三角形中邊長的關係、及其定理的證明。

勾股数

勾股数的發現時間较早，例如埃及的纸草书里面就有$(3,4,5)$这一组勾股数，而巴比伦泥板涉及的最大的一个勾股数组是$(13500,12709,18541)$。后来的中国的算經、印度与阿拉伯的数学书也有记载。在中国，《周髀算经》中也记述了$(3,4,5)$这一组勾股数；金朝数学家李冶在《测圆海镜》中，通过勾股容圆图式的十五个勾股形和直径的关系，建立了系統的天元术，推导出692条关于勾股形的各边的公式，其中用到了多组勾股数作为例子。

普遍定理的发现

巴比伦人得到的勾股数的数量和质量不太可能纯从测量手段获得。之后的毕达哥拉斯本人并无著作传世，不过在他死后一千年，5世纪的普罗克勒斯给欧几里德的名著《几何原本》做注解时将最早的发现和证明归功于毕达哥拉斯学派：

“ 如果我们听听那些喜欢说古代历史的人，他们把这个定理归于毕达哥拉斯，并且说他杀了一头公牛来庆祝。对我来说，虽然我欣赏那个第一个观察到这个定理的人，我更叹服《原本》的作者。不光是因为他给出了清晰明确的证明，而且还因为他用无可置疑的方法在第六篇中证明了一个更一般的命题。 ”

普魯塔克和西塞罗也将发现的功劳归于毕达哥拉斯，但没有任何证据表明毕达哥拉斯证明了勾股定理，以素食闻名的毕达哥拉斯杀牛更是不可思议。

在中国，记载秦朝的算数书并未记载勾股定理，只是记录了一些勾股数。定理首次载于书面则是在成书于西汉但内容收集整理自公元前一千多年以来的《周髀算经》“荣方问于陈子”一节中：

“ 若求邪至日者，以日下为句，日高为股，句股各自乘，并而開方除之，得邪至日。 ” —— 《周髀算经》卷上之二

因此有些人将这个定理称之为陈子定理。

东汉末年赵爽《周髀算经注》《勾股圆方图注》记载：

“ 勾股各自乘，并之，为弦实，开方除之，即弦。 ”

赵爽《勾股圆方图》

在《九章算术注》中，刘徽反复利用勾股定理求圆周率，并利用“割补术”做“青朱出入图”完成勾股定理的几何图形证明。

直至現時為止，仍有許多關於勾股定理是否不止一次被發現的辯論。

证明

毕达哥拉斯学派的证明没有流传下来，流传下来书面证明最早见于《几何原本》第一册的第47个命题。在中国，东汉末年吴国的赵爽最早给出勾股定理的证明。最近，巴勒蒂·克爾什納·蒂爾特吉在吠陀數學一書中聲稱古代印度教吠陀證明了勾股定理。

證明

這個定理有許多證明的方法，其證明的方法可能是數學眾多定理中最多的。路明思（Elisha Scott Loomis）的Pythagorean Proposition一書中總共提到367種證明方式。

有人會嘗試以三角恆等式（例如：正弦和餘弦函數的泰勒級數）來證明勾股定理，但是，因為所有的基本三角恆等式都是建基於勾股定理，所以不能作為勾股定理的證明（參見循環論證）。

趙爽勾股圆方图证明法

中国三国时期趙爽为证明勾股定理作“勾股圆方图”即“弦图”，按其证明思路，其法可涵盖所有直角三角形，为东方特色勾股定理无字证明法。2002年第24届国际数学家大会（ICM）在北京召开。中国邮政发行一枚邮资明信片，邮资图就是这次大会的会标—中国古代证明勾股定理的趙爽弦图。

趙爽 勾股圆方图证明勾股定理法动画

刘徽“割补术”证明法

中国魏晋时期数学家刘徽依据其“割补术”为证勾股定理另辟蹊径而作“青朱出入图”。刘徽描述此图，“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂。开方除之，即弦也。”其大意为，一个任意直角三角形，以勾宽作红色正方形即朱方，以股长作青色正方形即青方。将朱方、青方两个正方形对齐底边排列，再进行割补—以盈补虚，分割线内不动，线外则“各从其类”，以合成弦的正方形即弦方，弦方开方即为弦长。

刘徽 青朱出入图

利用相似三角形的證法

相似三角形的證明

有許多勾股定理的證明方式，都是基於相似三角形中兩邊長的比例。

設$ABC$為一直角三角形，直角於$\angle C$（看右圖）。從點$C$畫上三角形的高，並將此高與${\overline {AB}}$的交叉點稱之為$H$。此新$\bigtriangleup ACH$和原本的$\bigtriangleup ABC$相似，因為在兩個三角形中都有一個直角（這又是由於「高」的定義），而兩個三角形都有$A$這個共同角，由此可知第三隻角都是相等的。同樣道理，$\bigtriangleup CBH$和$\bigtriangleup ABC$也是相似的。這些相似關係衍生出以下的比率關係：

因為

${\overline {BC}}=a,{\overline {AC}}=b,{\mbox{ and }}{\overline {AB}}=c,\!$

所以

${\frac {a}{c}}={\frac {\overline {HB}}{a}}{\mbox{ and }}{\frac {b}{c}}={\frac {\overline {AH}}{b}}.\,$

可以寫成

$a^{2}=c\times {\overline {HB}}{\mbox{ and }}b^{2}=c\times {\overline {AH}}.\,$

綜合這兩個方程式，我們得到

$a^{2}+b^{2}=c\times {\overline {HB}}+c\times {\overline {AH}}=c\times ({\overline {HB}}+{\overline {AH}})=c^{2}.\,\!$

換句話說:

$a^{2}+b^{2}=c^{2}.\,\!$

歐幾里得的證法

《幾何原本》中的證明

在歐幾里得的《幾何原本》一書中给出勾股定理的以下証明。設$\bigtriangleup ABC$為一直角三角形，其中A為直角。從$A$點劃一直線至對邊，使其垂直於對邊。延长此線把對邊上的正方形一分為二，其面積分別與其餘兩個正方形相等。

在定理的證明中，我們需要如下四個輔助定理：

• 如果兩個三角形有兩組對應邊和這兩組邊所夾的角相等，則兩三角形全等。（SAS定理）
• 三角形面積是任一同底同高之平行四邊形面積的一半。
• 任意一個正方形的面積等於其二邊長的乘積。
• 任意一個矩形的面積等於其二邊長的乘積（據輔助定理3）。

證明的思路為：把上方的兩個正方形，透過等高同底的三角形，以其面積關係，轉換成下方兩個同等面積的長方形。

证明辅助图2

其證明如下：

1. 設$\triangle ABC$為一直角三角形，其直角為$\angle CAB$。
2. 其邊為${\overline {BC}}$、${\overline {AB}}$、和${\overline {CA}}$，依序繪成四方形$CBDE$、$BAGF$和$ACIH$。
3. 畫出過點$A$之${\overline {BD}}$、${\overline {CE}}$的平行線。此線將分別與${\overline {BC}}$和${\overline {DE}}$直角相交於$K$、$L$。
4. 分別連接${\overline {CF}}$、${\overline {AD}}$，形成兩個三角形$BCF$、$BDA$。
5. $\angle CAB$和$\angle BAG$都是直角，因此$C$、$A$和$G$都是共线的，同理可证$B$、$A$和$H$共线。
6. $\angle CBD$和$\angle FBA$皆為直角，所以$\angle ABD$相等於$\angle FBC$。
7. 因為${\overline {AB}}$和${\overline {BD}}$分別等於${\overline {FB}}$和${\overline {BC}}$，所以$\triangle ABD$必須全等於$\triangle FBC$。
8. 因為$A$與$K$和$L$在同一直线上，所以四方形$BDLK$必須二倍面積於$\triangle ABD$。
9. 因為$C$、$A$和$G$在同一直线上，所以正方形$BAGF$必須二倍面積於$\triangle FBC$。
10. 因此四邊形$BDLK$必須和$BAGF$有相同的面積=${\overline {AB}}^{2}$。
11. 同理可證，四邊形$CKLE$必須有相同的面積$ACIH={\overline {AC}}^{2}$。
12. 把這兩個結果相加，${\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}$
13. 由於${\overline {BD}}={\overline {KL}}$，${\overline {BD}}\times {\overline {BK}}+{\overline {KL}}\times {\overline {KC}}={\overline {BD}}\left({\overline {BK}}+{\overline {KC}}\right)={\overline {BD}}\times {\overline {BC}}$
14. 由於$CBDE$是個正方形，因此${\overline {AB}}^{2}+{\overline {AC}}^{2}={\overline {BC}}^{2}$。

此證明是於歐幾里得《幾何原本》一書第1.47節所提出的

由于这个定理的证明依赖于平行公理，而且从这个定理可以推出平行公理，很多人质疑平行公理是这个定理的必要条件，一直到十九世纪尝试否定第五公理的非欧几何出现。

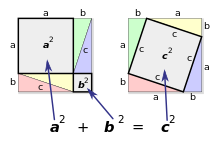
圖形重新排列證法

以面積減算法證明

此證明以圖形重新排列證明。兩個大正方形的面積皆為$(a+b)^{2}$。把四個相等的三角形移除後，左方餘下面積為$a^{2}+b^{2}$，右方餘下面積為$c^{2}$，兩者相等。證畢。

以重新排列法證明

以動畫方式來論證畢氏定理

勾股定理的逆定理

勾股定理的逆定理是判斷三角形為鈍角、銳角或直角的一個簡單的方法，其中${\overline {AB}}=c$為最長邊:

• 如果$a^{2}+b^{2}=c^{2}\,$，則$\triangle ABC$是直角三角形。
• 如果$a^{2}+b^{2}>c^{2}\,$，則$\triangle ABC$是銳角三角形（若無先前條件${\overline {AB}}=c$為最長邊，則該式的成立僅滿足$\angle C$是銳角）。
• 如果$a^{2}+b^{2}<c^{2}\,$，則$\triangle ABC$是鈍角三角形。

（這個逆定理其實只是餘弦定理的一個延伸）

逆定理的證明

勾股定理的逆定理的證法數明顯少於勾股定理的證法。以下是一些常見證法。

同一法

構造$\triangle A'B'C'$，使$a'=a,b'=b,\angle C'=90^{\operatorname {\mathrm {o} } }$。

根據勾股定理，$c'={\sqrt {a'^{2}+b'^{2}}}={\sqrt {a^{2}+b^{2}}}=c$，從而$\triangle A'B'C'\cong \triangle ABC(SSS)$。

因此，$\angle C=90^{\operatorname {\mathrm {o} } }$。

餘弦定理

根據餘弦定理，$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}$。由於$a^{2}+b^{2}=c^{2}\,$，故$\cos C=0\,$，從而$\angle C=90^{\operatorname {\mathrm {o} } }$。

相似三角形

在${\overline {AB}}$边上截取点$D$使$\angle DCB=\angle A$。

在$\triangle CDB\,$与$\triangle ACB\,$中，

$\angle B=\angle B,\angle DCB=\angle A\Rightarrow \triangle CDB\sim \triangle ACB$

。

從而，${\frac {\overline {BC}}{\overline {BA}}}={\frac {\overline {BD}}{\overline {BC}}}\Rightarrow {\overline {BD}}={\frac {a^{2}}{c}}$，以及${\frac {\overline {CD}}{\overline {AC}}}={\frac {\overline {CB}}{\overline {AB}}}\Rightarrow {\overline {CD}}={\frac {\overline {ab}}{c}}$。

另一方面，${\overline {AD}}={\overline {AB}}-{\overline {BD}}=c-{\frac {a^{2}}{c}}={\frac {b^{2}}{c}}$，故由${\frac {\overline {DC}}{\overline {AD}}}={\frac {\overline {BC}}{\overline {AC}}}={\frac {\overline {BD}}{\overline {CD}}}={\frac {a}{b}}$知，$\triangle ACD\sim \triangle CBD$。

因而，$\angle BDC=\angle CDA=90^{\operatorname {\mathrm {o} } }$，所以$\angle ACB=\angle CDB=90^{\operatorname {\mathrm {o} } }$。

非欧几何

主条目：非欧几里得几何

勾股定理是由欧几里得几何的公理推导出来的，其在非欧几里得几何中是不成立的。因为勾股定理的成立涉及到了平行公设。

外部連結

• 勾股定理（MathWorld）（英文）

參見

• 直角三角形
• 勾股数
• 余弦定理
• 青朱出入图
• 《史记·夏本纪》记载大禹治水：“陆行乘车，水行乘船，泥行乘橇，山行乘檋。左准绳，右规矩，载四时，以开九州，通九道，陂九泽，度九山。”其中的规和矩就是运用勾股定理的实用工具之一。