质数

质数，又称素数，指在大于1的自然数中，除了$1$和该数自身外，无法被其他自然数整除的数（也可定义为只有1与该数本身两个正因数的数）。大于1的自然数若不是质数，则称之为合数（也称为合成数）。例如，5是个质数，因为其正因数只有1与5。7是个质数，因为其正因数只有1与7。而4则是个合数，因为除了1与4外，2也是其正因数。6也是个合数，因为除了1与6外，2与3也是其正因数。算术基本定理确立了质数于数论里的核心地位：任何大于1的整数均可被表示成一串唯一质数之乘积。为了确保该定理的唯一性，1被定义为不是质数，因为在因式分解中可以有任意多个1（如3、$1\times 3$、$1\times 1\times 3$等都是3的有效因数分解）。

古希腊数学家欧几里得于公元前300年前后证明有无限多个质数存在（欧几里得定理）。现时人们已发现多种验证质数的方法。其中试除法比较简单，但需时较长：设被测试的自然数为$n$，使用此方法者需逐一测试2与${\sqrt {n}}$之间的质数，确保它们无一能整除$n$。对于较大或一些具特别形式（如梅森数）的自然数，人们通常使用较有效率的演算法测试其是否为质数（例如2^82589933-1是直至2024年4月为止已知最大的梅森质数，也是直至2024年4月为止已知最大的质数）。虽然人们仍未发现可以完全区别质数与合数的公式，甚至研究质数分布时相当有力的筛法也会碰到奇偶性问题（也就是多种筛法都无法区别质数跟两个质数相乘的合数的问题），但已建构了质数的分布模式（亦即质数在大数时的统计模式）。19世纪晚期得到证明的质数定理指出：一个任意自然数n为质数的机率反比于其数位（或$n$的对数）。

许多有关质数的问题依然未解，如哥德巴赫猜想（每个大于2的偶数可表示成两个素数之和）及孪生质数猜想（存在无穷多对相差2的质数）。这些问题促进了数论各个分支的发展，主要在于数字的解析或代数方面。质数被用于资讯科技里的几个程序中，如公钥加密利用了难以将大数分解成其质因数之类的性质。质数亦在其他数学领域里形成了各种广义化的质数概念，主要出现在代数里，如质元素及质理想。

定义和例子

一个自然数（如1、2、3、4、5、6等）若恰有两个正因数（1及此数本身），则称之为质数。大于1的自然数若不是质数，则称之为合数。

数字12不是质数，因为将12以每4个分成1组，恰可分成3组（也有其他分法）。11则无法分成数量都大于1且都相同的各组，而都会有剩馀。因此，11为质数。

在数字1至6间，数字2、3与5为质数，1、4与6则不是质数。1不是质数，其理由见下文。2是质数，因为只有1与2可整除该数。接下来，3亦为质数，因为1与3可整除3，3除以2会馀1。因此，3为质数。不过，4是合数，因为2是另一个（除1与4外）可整除4的数：

4 = 2 · 2

5又是个质数：数字2、3与4均不能整除5。接下来，6会被2或3整除，因为

6 = 2 · 3

因此，6不是质数。右图显示12不是质数：12 = 3 · 4。不存在大于2的偶数为质数，因为依据定义，任何此类数字$n$均至少有三个不同的因数，即1、2与$n$。这意指$n$不是质数。因此，“奇质数”系指任何大于2的质数。类似地，当使用一般的十进位制时，所有大于5的质数，其尾数均为1、3、7或9，因为尾数0、2、4、6、8为2的倍数，尾数为0或5的数字为5的倍数。

若$n$为一自然数，则1与$n$会整除$n$。因此，质数的条件可重新叙述为：一个数字为质数，若该数大于1，且没有

$2,3,\ldots ,n-1$

会整除$n$。另一种叙述方式为：一数$n>1$为质数，若不能写成两个整数$a$与$b$的乘积，其中这两数均大于1：

$n=a\cdot b$.

换句话说，$n$为质数，若$n$无法分成数量都大于1且都相同的各组。

由所有质数组成之集合通常标记为P或$\mathbb {P}$。

前168个质数（所有小于1000的质数）为2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, ...（OEIS数列A000040）。

算术基本定理

主条目：算术基本定理

质数对于数论与一般数学的重要性来自于“算术基本定理”。该定理指出，每个大于1的整数均可写成一个以上的质数之乘积，且除了质因数的排序不同外是唯一的。质数可被认为是自然数的“基本建材”，例如：

23244	= 2 · 2 · 3 · 13 · 149
	= 22 · 3 · 13 · 149. （22表示2的平方或2次方。）

如同此例一般，相同的因数可能出现多次。一个数n的分解：

$n=p_{1}\cdot p_{2}\cdot \ldots \cdot p_{t}$

成（有限多个）质因数$p_{1}$、$p_{2}$、……、$p_{t}$，称之为$n$的“因数分解”。算术基本定理可以重新叙述为，任一质数分解除了因数的排序外，都是唯一的。因此，尽管实务上存在许多质数分解演算法来分解较大的数字，但最后都会得到相同的结果。

若$p$为质数，且$p$可整除整数的乘积$ab$，则$p$可整除$a$或可整除$b$。此一命题被称为欧几里得引理，被用来证明质数分解的唯一性。

1是否为质数

最早期的希腊人甚至不将1视为是一个数字，因此不会认为1是质数。到了中世纪与文艺复兴时期，许多数学家将1纳入作为第一个质数。到18世纪中期，克里斯蒂安·哥德巴赫在他与李昂哈德·欧拉著名的通信里将1列为第一个质数，但欧拉不同意。然而，到了19世纪，仍有许多数学家认为数字1是个质数。例如，德里克·诺曼·雷默（Derrick Norman Lehmer）在他那最大达10,006,721的质数列表中，将1列为第1个质数。昂利·勒贝格据说是最后一个称1为质数的职业数学家。到了20世纪初，数学家开始认为1不是个质数，但反而作为“单位”此一特殊类别。

许多数学成果在称1为质数时，仍将有效，但欧几里何的算术基本定理（如上所述）则无法不重新叙述而仍然成立。例如，数字15可分解成3 · 5及 1 · 3 · 5；若1被允许为一个质数，则这两个表示法将会被认为是将15分解至质数的不同方法，使得此一定理的陈述必须被修正。同样地，若将1视为质数，埃拉托斯特尼筛法将无法正常运作：若将1视为质数，此一筛法将会排除掉所有1的倍数（即所有其他的数），只留下数字1。此外，质数有几个1所没有的性质，如欧拉函数的对应值，以及除数函数的总和。

历史

埃拉托斯特尼筛法是个找出在一特定整数以下的所有质数之简单演算法，由古希腊数学家埃拉托斯特尼于公元前3世纪发明。

在古埃及人的幸存纪录中，有迹象显示他们对质数已有部分认识：例如，在莱因德数学纸草书中的古埃及分数展开时，对质数与对合数有著完全不同的类型。不过，对质数有过具体研究的最早幸存纪录来自古希腊。公元前300年左右的《几何原本》包含与质数有关的重要定理，如有无限多个质数，以及算术基本定理。欧几里得亦展示如何从梅森质数建构出完全数。埃拉托斯特尼提出的埃拉托斯特尼筛法是用来计算质数的一个简单方法，虽然今天使用电脑发现的大质数无法使用这个方法找出。

希腊之后，到17世纪之前，质数的研究少有进展。1640年，皮埃尔·德·费马叙述了费马小定理（之后才被莱布尼茨与欧拉证明）。费马亦推测，所有具$2^{2^{n}}+1$形式的数均为质数（称之为费马数），并验证至$n=4$（即2¹⁶ + 1）不过，后来由欧拉发现，下一个费马数2³² + 1即为合数，且实际上其他已知的费马数都不是质数。法国修道士马兰·梅森发现有的质数具$2^{p}-1$的形式，其中$p$为质数。为纪念他的贡献，此类质数后来被称为梅森质数。

欧拉在数论中的成果，许多与质数有关。他证明无穷级数${\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\ldots$会发散。1747年，欧拉证明每个偶完全数都确实为$2^{p-1}(2^{p}-1)$的形式，其中第二个因数为梅森质数。

19世纪初，勒壤得与高斯独立推测，当$x$趋向无限大时，小于$x$的质数数量会趋近于${\frac {x}{\ln x}}$，其中$\ln x$为$x$的自然对数。黎曼于1859年有关ζ函数的论文中勾勒出一个程式，导出了质数定理的证明。其大纲由雅克·阿达马与夏尔-让·德拉瓦莱·普桑所完成，他们于1896年独立证明出质数定理。

证明一个大数是否为质数通常无法由试除法来达成。许多数学家已研究过大数的质数测试，通常局限于特定的数字形式。其中包括费马数的贝潘测试（1877年）、普罗丝定理（约1878年）、卢卡斯-莱默质数判定法（1856年起）及广义卢卡斯质数测试。较近期的演算法，如APRT-CL、ECPP及AKS等，均可作用于任意数字上，但仍慢上许多。

长期以来，质数被认为在纯数学以外的地方只有极少数的应用。到了1970年代，发明公共密钥加密这个概念之后，情况改变了，质数变成了RSA加密演算法等一阶演算法之基础。

自1951年以来，所有已知最大的质数都由电脑所发现。对更大质数的搜寻已在数学界以外的地方产生出兴趣。网际网路梅森质数大搜索及其他用来寻找大质数的分散式运算计画变得流行，在数学家仍持续与质数理论奋斗的同时。

素数的数目

主条目：欧几里得定理

存在无限多个质数。另一种说法为，质数序列

2, 3, 5, 7, 11, 13, ...

永远不会结束。此一陈述被称为“欧几里得定理”，以古希腊数学家欧几里得为名，因为他提出了该陈述的第一个证明。已知存在其他更多的证明，包括欧拉的分析证明、哥德巴赫依据费马数的证明、弗斯滕伯格使用一般拓扑学的证明，以及库默尔优雅的证明。

欧几里得的证明

欧几里得的证明取任一个由质数所组成的有限集合$S$。该证明的关键想法为考虑$S$内所有质数相乘后加一的一个数字：

$N=1+\prod _{p\in S}p$。

如同其他自然数一般，$N$可被至少一个质数整除（即使N本身为质数亦同）。

任何可整除N的质数都不可能是有限集合$S$内的元素（质数），因为后者除N都会馀1。所以，$N$可被其他质数所整除。因此，任一个由质数所组成的有限集合，都可以扩展为更大个由质数所组成之集合。

这个证明通常会被错误地描述为，欧几里得一开始假定一个包含所有质数的集合，并导致矛盾；或者是，该集合恰好包含n个最小的质数，而不任意个由质数所组成之集合。今日，$n$个最小质数相乘后加一的一个数字，被称为第$n$个欧几里得数。

欧拉的解析证明

欧拉的证明使用到质数倒数的总和

$S(p)={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots +{\frac {1}{p}}$。

当$p$够大时，该和会大于任意实数。这可证明，存在无限多个质数，否则该和将只会增长至达到最大质数$p$为止。$S(p)$的增加率可使用梅滕斯第二定理来量化。比较总和

${\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}=\sum _{i=1}^{n}{\frac {1}{i^{2}}}$

当$n$趋向无限大时，此和不会变成无限大（见巴塞尔问题）。这意味著，质数比自然数的平方更常出现。布朗定理指出，孪生质数倒数的总和

$\left({{\frac {1}{3}}+{\frac {1}{5}}}\right)+\left({{\frac {1}{5}}+{\frac {1}{7}}}\right)+\left({{\frac {1}{11}}+{\frac {1}{13}}}\right)+\cdots =\sum \limits _{\begin{smallmatrix}p{\text{ prime, }}\\p+2{\text{ prime}}\end{smallmatrix}}{\left({{\frac {1}{p}}+{\frac {1}{p+2}}}\right)},$

是有限的。

测试质数与整数分解

确认一个数$n$是否为质数有许多种方法。最基本的程序为试除法，但因为速率很慢，没有什么实际用处。有一类现代的质数测试可适用于任意数字之上，另有一类更有效率的测试方法，则只能适用于特定的数字之上。大多数此类方法只能辨别$n$是否为质数。也能给出$n$的一个（或全部）质因数之程序称之为因数分解演算法。

试除法

主条目：试除法

测试$n$是否为质数的最基本方法为试除法。此一程序将n除以每个大于1且小于等于$n$的平方根之整数$m$。若存在一个相除为整数的结果，则$n$不是质数；反之则是个质数。实际上，若$n=ab$是个合数（其中$a$与$b\neq 1$），则其中一个因数$a$或$b$必定至大为${\sqrt {n}}$。例如，对$n=37$使用试除法，将37除以$m=2,3,4,5,6$，没有一个数能整除37，因此37为质数。此一程序若能知道直至${\sqrt {n}}$的所有质数列表，则可以只检查$m$为质数的状况，以提升效率。例如，为检查37是否为质数，只有3个相除是必要的（$m=2,3,5$），因为4与6为合数。

作为一个简单的方法，试除法在测试大整数时很快地会变得不切实际，因为可能的因数数量会随著n的增加而迅速增加。依据下文所述之质数定理，小于${\sqrt {n}}$的质数之数量约为${\frac {\sqrt {n}}{\ln {\sqrt {n}}}}$，因此使用试除法测试$n$是否为质数时，大约会需要用到这么多的数字。对$n=10^{20}$，此一数值约为4.5亿，对许多实际应用而言都太过庞大。

筛法

一个能给出某个数值以下的所有质数之演算法，称之为质数筛法，可用于只使用质数的试除法内。最古老的一个例子为埃拉托斯特尼筛法（见上文），至今仍最常被使用。阿特金筛法为另外一例。在电脑出现之前，筛法曾被用来给出10⁷以下的质数列表。

质数测试与质数证明

主条目：素性测试

现代测试一般的数字$n$是否为质数的方法可分成两个主要类型，随机（或“蒙特卡洛”）与确定性演算法。确定性演算法可肯定辨别一个数字是否为质数。例如，试除法即是个确定性演算法，因为若正确执行，该方法总是可以辨别一个质数为质数，一个合数为合数。随机演算法一般比较快，但无法完全证明一个数是否为质数。这类测试依靠部分随机的方法来测试一个给定的数字。例如，一测试在应用于质数时总是会通过，但在应用于合数时通过的机率为$p$。若重复这个测试$n$次，且每次都通过，则该数为合数的机率为${\frac {1}{(1-p)^{n}}}$，会随著测试次数呈指数下滑，因此可越来越确信（虽然总是无法完全确信）该数为质数。另一方面，若测试曾失败过，则可知该数为合数。

随机测试的一个特别简单的例子为费马质数判定法，使用到对任何整数$a$，$n^{p}\equiv n(\mod p)$，其中$p$为质数的这个事实（费马小定理）。若想要测试一个数字$b$是否为质数，则可随机选择$n$来计算$n^{b}(\mod b)$的值。这个测试的缺点在于，有些合数（卡迈克尔数）即使不是质数，也会符合费马恒等式，因此这个测试无法辨别质数与卡迈克尔数，最小的三个卡迈克尔数为561，1105，1729。卡迈克尔数比质数还少上许多，所以这个测试在实际应用上还是有用的。费马质数判定法更强大的延伸方法，包括贝利-PSW、米勒-拉宾与Solovay-Strassen质数测试，都保证至少在应用于合数时，有部分时候会失败。

确定性演算法不会将合数错误判定为质数。在实务上，最快的此类方法为椭圆曲线质数证明。其运算时间是透过实务分析出来的，不像最新的AKS质数测试，有已被严格证明出来的复杂度。确定性演算法通常较随机演算法来得慢，所以一般会先使用随机演算法，再采用较费时的确定性演算法。

下面表格列出一些质数测试。运算时间以被测试的数字$n$来表示，并对随机演算法，以$k$表示其测试次数。此外，$\varepsilon$是指一任意小的正数，$\log$是指一无特定基数的对数。大O符号表示，像是在椭圆曲线质数证明里，所需之运算时间最长为一常数（与n无关，但会与ε有关）乘于log^5+ε(n)。

测试	发明于	类型	运算时间	注记
AKS质数测试	2002	确定性	$O(\log ^{6+\varepsilon }(n))$
椭圆曲线质数证明	1977	确定性	$O(\log ^{5+\varepsilon }(n))$“实务分析”
贝利-PSW质数测试	1980	随机	$O(\log ^{3}n)$	无已知反例
米勒-拉宾质数判定法	1980	随机	$O(k\cdot \log ^{2+\varepsilon }(n))$	错误机率$4^{-k}$
Solovay-Strassen质数	1977	随机	$O(k\cdot \log ^{3}n)$	错误机率$2^{-k}$
费马质数判定法		随机	$O(k\cdot \log ^{2+\varepsilon }(n))$	遇到卡迈克尔数时会失败

专用目的演算法与最大已知质数

更多信息：质数列表

建构正五边形。5是个费马质数。

除了前述可应用于任何自然数n之上的测试外，一些更有效率的质数测试适用于特定数字之上。例如，卢卡斯质数测试需要知道n − 1的质因数，而卢卡斯-莱默质数测试则需要以n + 1的质因数作为输入。例如，这些测试可应用在检查

n! ± 1 = 1 · 2 · 3 · ... · n ± 1

是否为一质数。此类形式的质数称之为阶乘质数。其他具p+1或p-1之类形式的质数还包括索菲·热尔曼质数（具2p+1形式的质数，其中p为质数）、质数阶乘质数、费马质数与梅森质数（具2^p − 1形式的质数，其中p为质数）。卢卡斯-雷默质数测试对这类形式的数特别地快。这也是为何自电脑出现以来，最大已知质数总会是梅森质数的原因。

费马质数具下列形式

F_k = 2^2k + 1,

其中，k为任意自然数。费马质数以皮埃尔·德·费马为名，他猜想此类数字F_k均为质数。费马认为F_k均为质数的理由为此串列的前5个数字（3、5、17、257及65537）为质数。不过，F₅却为合数，且直至2015年发现的其他费马数字也全都是合数。一个正n边形可用尺规作图，若且唯若

n = 2ⁱ · m

其中，m为任意个不同费马质数之乘积，及i为任一自然数，包括0。

下列表格给出各种形式的最大已知质数。有些质数使用分散式计算找到。2009年，网际网路梅森质数大搜索因为第一个发现具至少1,000万个数位的质数，而获得10万美元的奖金。电子前哨基金会亦为具至少1亿个数位及10亿个数位的质数分别提供15万美元及25万美元的奖金。

类型	质数	数位	日期	发现者
梅森质数	282589933 − 1	23,249,425	2018年12月21日	网际网路梅森质数大搜索
非梅森质数（普罗斯数）	19,249×213,018,586 + 1	3,918,990	2007年3月26日	十七或者破产
阶乘质数	150209! + 1	712,355	2011年10月	PrimeGrid
质数阶乘质数	1098133# - 1	476,311	2012年3月	PrimeGrid
孪生质数s	3756801695685×2666669 ± 1	200,700	2011年12月	PrimeGrid

整数分解

主条目：整数分解

给定一合数n，给出一个（或全部）质因数的工作称之为n的因数分解。椭圆曲线分解是一个依靠椭圆曲线上的运算来分解质因数的演算法。

质数分布

1975年，数论学家唐·察吉尔评论质数

像生长于自然数间的杂草，似乎不服从机率之外的法则，（但又）表现出惊人的规律性，并有规范其行为之法则，且以军事化的精准度遵守著这些法则。

大质数的分布，如在一给定数值以下有多少质数这个问题，可由质数定理所描述；但有效描述第n个质数的公式则仍未找到。

存在任意长的连续非质数数列，如对每个正整数$n$，从$(n+1)!+2$至$(n+1)!+n+1$的$n$个连续正整数都会是合数（因为若$k$为2至$n+1$间的一整数，$(n+1)!+k$就可被k整除）。

狄利克雷定理表示，取两个互质的整数a与b，其线性多项式

$p(n)=a+bn\,$

会有无限多个质数值。该定理亦表示，这些质数值的倒数和会发散，且具有相同b的不同多项式会有差不多相同的质数比例。

有关二次多项式的相关问题则尚无较好之理解。

质数的公式

主条目：质数公式

对于质数，还没有一个已知的有效公式。例如，米尔斯定理与赖特所提的一个定理表示，存在实常数A>1与μ，使得

$\left\lfloor A^{3^{n}}\right\rfloor {\text{ and }}\left\lfloor 2^{\dots ^{2^{2^{\mu }}}}\right\rfloor$

对任何自然数n而言，均为质数。其中，$\lfloor -\rfloor$为高斯符号，表示不大于符号内数字的最大整数。第二个公式可使用伯特兰-切比雪夫定理得证（由切比雪夫第一个证得）。该定理表示，总是存在至少一个质数p，使得 n < p < 2n − 2，其中n为大于3的任一自然数。第一个公式可由威尔逊定理导出，每个不同的n会对应到不同的质数，除了数字2会有多个n对应到外。不过，这两个公式都需要先计算出A或μ的值来。

不存在一个只会产生质数值的非常数多项式，即使该多项式有许多个变数。不过，存在具9个变数的丢番图方程，其参数具备以下性质：该参数为质数，若且唯若其方程组有自然数解。这可被用来获得其所有“正值”均为质数的一个公式。

一特定数以下的质数之数量

主条目：质数定理和质数计算函数

图中的曲线分别表示π(n)（蓝）、n / ln (n)（绿）与Li(n)（红）。

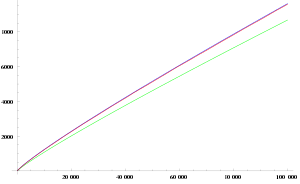
质数计算函数π(n)被定义为不大于n的质数之数量。例如，π(11) = 5，因为有5个质数小于或等于11。已知有演算法可比去计算每个不大于n的质数更快的速率去计算π(n)的值。质数定理表示，π(n)的可由下列公式近似给出：

$\pi (n)\approx {\frac {n}{\ln n}},$

亦即，π(n)与等式右边的值在n趋近于无限大时，会趋近于1。这表示，小于n的数字为质数的可能性（大约）与n的数位呈正比。对π(n)更精确的描述可由对数积分给出：

$\operatorname {Li} (n)=\int _{2}^{n}{\frac {dt}{\ln t}}$。

质数定理亦蕰涵著对第n个质数p_n（如p₁ = 2、p₂ = 3等）的大小之估算：当数字大到某一程度时，p_n的值会变得约略为n log(n)。特别的是，质数间隙，即两个连续质数p_n与p_n+1间的差会变得任意地大。后者可由数列 n! + 2, n! + 3,…, n! + n（其中n为任一自然数）看出。

等差数列

等差数列是指由被一固定数（模）q除后会得到同一馀数的自然数所组成之集合。例如：

3, 12, 21, 30, 39, ...,

是一个等差数列，模q = 9。除了3以外，其中没有一个数会是质数，因为3 + 9n = 3(1 + 3n)，所以此一数列里的其他数字均为合数。（一般来所有大于q的质数都具有q#·n + m的形式，其中0 < m < q#，且m没有不大于q的质因数。）因此，数列

a, a + q, a + 2q, a + 3q,…

只在a与q 互质（其最大公因数为1）之时，可以有无限多个质数。若满足此一必要条件，狄利克雷定理表示，该数列含有无限多个质数。下图描述q = 9时的情形：数字每遇到9的倍数就会再再由下往上缠一次。质数以红底标记。行（数列）开始于a = 3, 6, 9者至多只包含一个质数。其他行（a = 1, 2, 4, 5, 7, 8）则均包含无限多个质数。更甚之，质数以长期来看，会均匀分布于各行之中，亦即每个质数模9会与6个数其中一数同馀的机率均为1/6。

质数（以红底标计）在模9的等差数列中。

格林-陶定理证明，存在由任意多个质数组成的等差数列。一个奇质数p可表示成两个平方数之和p = x² + y²，若且唯若p同馀于1模4（费马平方和定理）。

二次多项式的质数值

乌岚螺旋。红点表示质数。具4n² − 2n + 41形式的质数则以蓝点标记。

欧拉指出函数

$n^{2}+n+41\,$

于　0 ≤ n < 40时会给出质数，此一事实导致了艰深的代数数论，或更具体地说为黑格纳数。当n更大时，该函数会给出合数值。哈代- 李特伍德猜想（Hardy-Littlewood conjecture）能给出一个有关具整数系数a、b与c的二次多项式

$f(n)=ax^{2}+bx+c\,$

的值为质数之机率的一个渐近预测，并能以对数积分Li(n)及系数a、b、c来表示。不过，该程式已被证实难以取得：仍未知是否存在一个二次多项式（a ≠ 0）能给出无限多个质数。乌岚螺旋将所有自然数以螺旋的方法描绘。令人惊讶的是，质数会群聚在某些对角线上，表示有些二次多项式会比其他二次多项式给出更多个质数值来。

未解决的问题

ζ函数与黎曼猜想

主条目：黎曼猜想

ζ函数ζ(s)的图。在s=1时，该函数会有极点，亦即会趋近于无限大。

黎曼ζ函数ζ(s)被定义为一无穷级数

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}},$

其中，s为实数部分大于1的一个复数。由算术基本定理可证得，该级数会等于下面的无穷乘积

$\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}$。

ζ函数与质数密切相关。例如，存在无限多个质数这个事实也可以使用ζ函数看出：若只有有限多个质数，则ζ(1)将会是个有限值。不过，调和级数1 + 1/2 + 1/3 + 1/4 + ...会发散，所以必须有无限多个质数。另一个能看见ζ函数的丰富性，并一瞥现代代数数论的例子为下面的恒等式（巴塞尔问题，由欧拉给出）：

$\zeta (2)=\prod _{p}{\frac {1}{1-p^{-2}}}={\frac {\pi ^{2}}{6}}$。

ζ(2)的倒数6/π²，是两个随机选定的数字会互质的机率。

未被证明的“黎曼猜想”，于1859年提出，表示除s = −2, −4, ...,外，ζ函数所有的根，其实数部分均为1/2。此一猜想与质数间的关连在于，该猜想实际上是在说，质数在正整数中出现频率和统计学的随机不同；若假设为真，质数计算函数便可有效掌握，在大数时不再需要近似求值。从物理的观点来看，这大约是在说，质数分布的不规则性仅来自于随机的杂讯。从数学的观点来看，则大约是在说，质数的渐近分布（质数定理表示小于x的质数约有x/log x个）在x周围的区间内，于区间长度远小于x的平方根时亦成立。此一猜想一般认为是正确的。

其他猜想

更多信息：分类:素数猜想

除了黎曼猜想之外，还有许多其他的猜想存在。虽然这些猜想的陈述大多很简单，但许多猜想经过了数十年仍提不出证明，如4个兰道问题，从1912年提出至今仍然未解。其中一个为哥德巴赫猜想，该猜想认为每个大于2的偶数n都可表示成两个质数之和。至于2011年2月，这个猜想对最大达n = 2 · 10¹⁷的所有数字都会成立。较弱形式的哥德巴赫猜想已被证明，如维诺格拉多夫定理，该定理表示每个足够大的奇数都可表示成三个质数之和。陈氏定理表示，每个足够大的偶数都可表示成一个质数与一个半质数（两个质数的乘积）之和。此外，任一个偶数均可写成六个质数之和。数论研究这些问题的分支称之为加法数论。反哥德巴赫猜想，所有的正偶数n都可以表示成两个质数之差，但此猜想可由波利尼亚克猜想类推证明。

其他猜想处理是否有无限多个具某些限制的质数这类问题。据猜想，存在无限多个费波那契质数与无限多个梅森质数，但没有无限多个费马质数。还不知道是否存在无限多个维费里希质数与欧几里得质数。

第三种类型的猜想涉及到质数的分布情形。据猜想，存在无限多对孪生质数，即有无限多对相差2的质数（孪生质数猜想）。波利尼亚克猜想是比孪生质数猜想更强的一个猜想，该猜想表示存在无限多对相差2n的连续质数。据猜想，存在无限多个具n² + 1形式的质数。上述猜想都是申策尔猜想的特例。布罗卡猜想表示，在两个大于2的连续质数之平方数之间，总是会有至少4个质数。勒让德猜想表示，对每个正整数n，n²与(n + 1)²间总会存在一个质数。克拉梅尔猜想可导出勒让德猜想。

应用

长期以来，数论，尤其是对质数的研究，一般都会被认为是典型的纯数学，除了求知的趣味之外，没有其他应用。特别是，一些数论学家，如英国数学家戈弗雷·哈罗德·哈代即对其工作绝对不会有任何在军事上的重大性感到自豪。然而，此一观点在1970年代时遭到粉碎，当质数被公开宣布可以作为产生公钥加密演算法的基础之时。质数现在也被用在杂凑表与伪乱数产生器里。

旋转机被设计成在每个转片上有不同数目的销，在每个转片上的销的数量都会是质数，亦或是会与其他转片上的销的数量互质。这有助于在重复所有的组合之前，让所有转片的可能组合都能出现过一次。

国际标准书号的最后一码为校验码，其演算法使用到了11是个质数的这个事实。

在汽车变速箱齿轮的设计上，相邻的两个大小齿轮齿数最好设计成素数，以增加两齿轮内两个相同的齿相遇啮合次数的最小公倍数，可增强耐用度减少故障。

在害虫的生物生长周期与杀虫剂使用之间的关系上，杀虫剂的素数次数的使用也得到了证明。实验表明，素数次数地使用杀虫剂是最合理的：都是使用在害虫繁殖的高潮期，而且害虫很难产生抗药性。

以素数形式无规律变化的导弹和鱼雷可以使敌人不易拦截。

模一质数与有限体之运算

主条目：模运算

“模运算”使用下列数字修改了一般的运算

$\{0,1,2,\dots ,n-1\},\,$

其中n是个固定的自然数，称之为“模”。计算加法、减法及乘法都与一般的运算一样，不过负数或大于n − 1的数字出现时，会被除以n所得的馀数取代。例如，对n=7，3+5为1，而不是8，因为8除以7馀1。这通常念为“3+5同馀于1模7”，并标记为

$3+5\equiv 1{\pmod {7}}$。

同样地，6 + 1 ≡ 0 (mod 7)、2 - 5 ≡ 4 (mod 7)，因为 -3 + 7 = 4，以及3 · 4 ≡ 5 (mod 7)，因为12除以7馀5。加法与乘法在整数里常见的标准性质在模运算里也依然有效。使用抽象代数的说法，由上述整数所组成之集合，亦标记为Z/nZ，且因此为一可交换环。不过，除法在模运算里不一定都是可行的。例如，对n=6，方程

$3\cdot x\equiv 2{\pmod {6}},$

的解x会类比于2/3，无解，亦可透过计算3 · 0、...、3 · 5模6看出。不过，有关质数的不同性质如下：除法在模运算里是可行的，若且唯若n为质数。等价地说，n为质数，若且唯若所有满足2 ≤ m ≤ n − 1的整数m都会与n 互质，亦即其公因数只有1。实际上，对n=7，方程

$3\cdot x\equiv 2\ \ (\operatorname {mod} \ 7),$

会有唯一的解x = 3。因此，对任何质数p，Z/pZ（亦标记为F_p）也会是个体，或更具体地说，是个有限体，因为该集合包含有限多（即p）个元素。

许多定理可以透过从此一抽象的方式检查F_p而导出。例如，费马小定理表示

$a^{p-1}\equiv 1(\operatorname {mod} \ p)$

，其中a为任一不被p整除的整数。该定理即可使用这些概念证得。这意味著

$\sum _{a=1}^{p-1}a^{p-1}\equiv (p-1)\cdot 1\equiv -1{\pmod {p}}$。

吾乡-朱加猜想表示，上述公式亦是p为质数的必要条件。另一个费马小定理的推论如下：若p为2与5之外的其他质数，¹/_p总是个循环小数，其周期为p − 1或p − 1的因数。分数¹/_p依q（10以外的整数）为基底表示亦有类似的效果，只要p不是q的质因数的话。威尔逊定理表示，整数p > 1为质数，若且唯若阶乘 (p − 1)! + 1可被p整除。此外，整数n > 4为合数，若且唯若 (n − 1)!可被n整除。

其他数学里出现的质数

许多数学领域里会大量使用到质数。举有限群的理论为例，西罗定理即是一例。该定理表示，若G是个有限群，且pⁿ为质数p可整除G的阶的最大幂次，则G会有个pⁿ阶的子群。此外，任意质数阶的群均为循环群（拉格朗日定理）。

公开金钥加密

主条目：公开金钥加密

几个公开金钥加密演算法，如RSA与迪菲－赫尔曼金钥交换，都是以大质数为其基础（如512位元的质数常被用于RSA里，而1024位元的质数则一般被迪菲-赫尔曼金钥交换所采用）。RSA依靠计算出两个（大）质数的相乘会比找出相乘后的数的两个质因数容易出许多这个假设。迪菲－赫尔曼金钥交换依靠存在模幂次的有效演算法，但相反运算的离散对数仍被认为是个困难的问题此一事实。

自然里的质数

周期蝉属里的蝉在其演化策略上使用到质数。蝉会在地底下以幼虫的形态度过其一生中的大部分时间。周期蝉只会在7年、13年或17年后化蛹，然后从洞穴里出现、飞行、交配、产卵，并在至多数周后死亡。此一演化策略的原因据信是因为若出现的周期为质数年，掠食者就很难演化成以周期蝉为主食的动物。若周期蝉出现的周期为非质数年，如12年，则每2年、3年、4年、6年或12年出现一次的掠食者就一定遇得到周期蝉。经过200年以后，假设14年与15年出现一次的周期蝉，其掠食者的平均数量，会比13年与17年出现一次的周期蝉，高出2%。虽然相差不大，此一优势似乎已足够驱动天择，选择具质数年生命周期的这些昆虫。

据猜测，ζ函数的根与复数量子系统的能阶有关。

推广

质数的概念是如此的重要，以致此一概念被以不同方式推广至数学的不同领域里去。通常，“质”（prime）可在适当的意义下，用来表示具有最小性或不可分解性。例如，质体是指一个包含0与1的体F的最小子体。质体必为有理数或具有p个元素的有限体，这也是其名称的缘由。若任一物件基本上均可唯一地分解成较小的部分，则这些较小的部分也会用“质”这个字来形容。例如，在纽结理论里，质纽结是指不可分解的纽结，亦即该纽结不可写成两个非平凡纽结的连通和。任一纽结均可唯一地表示为质纽约的连通和。质模型与三维质流形亦为此类型的例子。

环内的素元

主条目：素元和不可约元素

质数应用于任一可交换环R（具加法、减法与乘法的代数结构）的元素，可产生两个更为一般的概念：“素元”与“不可约元素”。R的元素称为素元，若该元素不为0或单位元素，且给定R内的元素x与y，若p可除以xy，则p可除以x或y。一元素称为不可约元素，若该元素不为单位元素，且无法写成两个不是单位元素之环元素的乘积。在整数环Z里，由素元所组成的集合等于由不可约元素所组成的集合，为

$\{\dots ,-11,-7,-5,-3,-2,2,3,5,7,11,\dots \}\,$。

在任一环R里，每个素元都是不可约元素。反之不一定成立，但在唯一分解整环里会成立。

算术基本定理在唯一分解整环里仍然成立。此类整环的一个例子为高斯整数Z[i]，由具a + bi（其中a与b为任意整数）形式的复数所组成之集合。其素元称之为“高斯质数”。不是所有的质数都是高斯质数：在这个较大的环Z[i]之中，2可被分解成两个高斯质数 (1 + i)与 (1 - i)之乘积。有理质数（即在有理数里的素元），具4k+3形式者为高斯素数；具4k+1形式者则不是。

质理想

主条目：质理想

在环论里，数的概念一般被理想所取代。“质理想”广义化了质元素的概念，为由质元素产生的主理想，是在交换代数、代数数论与代数几何里的重要工具与研究对象。整数环的质理想为理想 (0)、(2)、(3)、(5)、(7)、(11)、…算术基本定理被广义化成准素分解，可将每个在可交换诺特环里的理想表示成准素理想（为质数幂次的一适合广义化）的交集。

透过环的谱这个概念，质理想成为代数几何物件的点。算术几何也受益于这个概念，且许多概念会同时存在于几何与数论之内。例如，对一扩张体的质理想分解（这是代数数论里的一个基本问题），与几何里的分歧具有某些相似之处。此类分歧问题甚至在只关注整数的数论问题里也会出现。例如，二次体的整数环内的质理想可被用来证明二次互反律。二次互反律讨论下面二次方程

$x^{2}\equiv p\ \ ({\text{mod }}q),\,$

是否有整数解，其中x为整数，p与q为（一般）质数。早期对费马最后定理证明之尝试，于恩斯特·库默尔引入正则素数后达到了高潮。正则质数是指无法在由下列式子（其中a₀、…、a_p−1为整数，ζ则是能使ζ^p = 1的复数）

$a_{0}+a_{1}\zeta +\cdots +a_{p-1}\zeta ^{p-1}\,,$

组成的环里，使得唯一分解定理失效的质数。

赋值

赋值理论研究由一个体K映射至实数R的某个函数（称之为赋值）。每个此类赋值都能给出一个 K上的拓扑，且两个赋值被称为等价，若两者有相同拓扑。K的质数为一赋值的等价类。例如，一个有理数q的p进赋值被定义为整数v_p(q)，使得

$q=p^{v_{p}(q)}{\frac {r}{s}},$

其中r与s不被p所整除。例如，v₃(18/7) = 2。p进范数被定义为

$\left|q\right|_{p}:=p^{-v_{p}(q)}.\,$

特别的是，当一个数字乘上p时，其范数会变小，与一般的绝对赋值（亦称为无限质数）形成明显的对比。当透过绝对赋值完备有理数会得出由实数所组成的体，透过p进范数完备有理数则会得出由p进数所组成的体。实际上，依据奥斯特洛夫斯基定理，上述两种方法是完备有理数的所有方法。一些与有理数或更一般化之大域体有关的算术问题，可能可以被转换至完备（或局部）体上。此一局部-全域原则再次地强调了质数对于数论的重要性。

在艺术与文学里

质数也影响了许多的艺术家与作家。法国作曲家奥立佛·梅湘使用质数创造出无节拍音乐。在《La Nativite du Seigneur》与《Quatre etudes de rythme》等作品里，梅湘同时采用由不同质数给定之长度的基调，创造出不可预测的节奏：第三个练习曲《Neumes rythmiques》中出现了质数41、43、47及53。据梅湘所述，此类作曲方式是“由自然的运动，自由且不均匀的持续运动中获得的灵感”。

NASA科学家卡尔·萨根在他的科幻小说《接触未来》（Contact）里，认为质数可作为与外星人沟通的一种方式。这种想法是他与美国天文学家法兰克·德雷克于1975年闲聊时形成的。

许多电影，如《异次元杀阵》（Cube）、《神鬼尖兵》（Sneakers）、《越爱越美丽》（The Mirror Has Two Faces）及《美丽境界》（A Beautiful Mind），均反映出大众对质数与密码学之神秘的迷恋。保罗·裘唐诺所著的小说《质数的孤独》（The Solitude of Prime Numbers）里，质数被用来比喻寂寞与孤独，被描述成整数之间的“局外人”。

荒木飞吕彦所创作的日本漫画《JoJo的奇妙冒险》第六部《石之海》的反派普奇神父喜欢数质数，他认为质数是孤独的数字，并透过数质数安抚他紧张的情绪。

另见

• 阿德曼-波门伦斯-鲁梅利质数测试
• Bonse不等式
• 布朗筛法
• 伯恩赛德定理
• 契博塔耶夫密度定理
• 中国馀数定理
• 卡伦数
• 非法质数
• 质数列表
• 梅森质数
• 可乘数论
• 普通数域筛选法
• 贝潘测试
• 实际数
• 质k元组
• 自由黎曼气体
• 二次剩馀问题
• RSA数
• 光滑数
• 超质数
• 胡道尔数
• 幸运素数
• 素数判定法则
• 埃拉托斯特尼筛法
• 孪生素数
• 三胞胎素数
• PrimeGrid
• GIMPS
• 质数大富豪

参考资料

• Apostol, Thomas M., Introduction to Analytic Number Theory, New York: Springer, 1976, ISBN 0-387-90163-9 
• Conway, John Horton; Guy, Richard K., The Book of Numbers, New York: Copernicus, 1996, ISBN 978-0-387-97993-9 
• Crandall, Richard; Pomerance, Carl, Prime Numbers: A Computational Perspective 2nd, Berlin, New York: Springer-Verlag, 2005, ISBN 978-0-387-25282-7 
• Derbyshire, John, Prime obsession, Joseph Henry Press, Washington, DC, 2003, ISBN 978-0-309-08549-6, MR 1968857 
• Eisenbud, David, Commutative algebra, Graduate Texts in Mathematics 150, Berlin, New York: Springer-Verlag, 1995, ISBN 978-0-387-94268-1, MR 1322960 
• Fraleigh, John B., A First Course In Abstract Algebra 2nd, Reading: Addison-Wesley, 1976, ISBN 0-201-01984-1 
• Furstenberg, Harry, On the infinitude of primes, The American Mathematical Monthly (Mathematical Association of America), 1955, 62 (5): 353, JSTOR 2307043, doi:10.2307/2307043 
• Green, Ben; Tao, Terence, The primes contain arbitrarily long arithmetic progressions, Annals of Mathematics, 2008, 167 (2): 481–547, arXiv:math.NT/0404188 , doi:10.4007/annals.2008.167.481 
• Gowers, Timothy, Mathematics: A Very Short Introduction, Oxford University Press, 2002, ISBN 978-0-19-285361-5 
• Guy, Richard K., Unsolved Problems in Number Theory, Berlin, New York: Springer-Verlag, 1981, ISBN 978-0-387-90593-8 
• Havil, Julian, Gamma: Exploring Euler's Constant, Princeton University Press, 2003, ISBN 978-0-691-09983-5 
• Hardy, Godfrey Harold, A Course of Pure Mathematics, Cambridge University Press, 1908, ISBN 978-0-521-09227-2 
• Hardy, Godfrey Harold, A Mathematician's Apology, Cambridge University Press, 1940, ISBN 978-0-521-42706-7 
• Herstein, I. N., Topics In Algebra, Waltham: Blaisdell Publishing Company, 1964, ISBN 978-1114541016 
• Hill, Peter Jensen (编), The Messiaen companion, Portland, Or: Amadeus Press, 1995, ISBN 978-0-931340-95-6 
• Hua, L.K., Additive Theory of Prime Numbers, Translations of Mathematical Monographs 13, Providence, RI: American Mathematical Society: 176–177, 2009 [1965], ISBN 978-0821849422, MR 0194404, OCLC 824812353 
• Lehmer, D. H., Factor table for the first ten millions containing the smallest factor of every number not divisible by 2, 3, 5, or 7 between the limits 0 and 10017000, Washington, D.C.: Carnegie Institution of Washington, 1909 
• McCoy, Neal H., Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, 1968, LCCN 68-15225 
• Narkiewicz, Wladyslaw, The development of prime number theory: from Euclid to Hardy and Littlewood, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, 2000, ISBN 978-3-540-66289-1 
• Ribenboim, Paulo, The little book of bigger primes, Berlin, New York: Springer-Verlag, 2004, ISBN 978-0-387-20169-6 
• Riesel, Hans, Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, 1994, ISBN 978-0-8176-3743-9 
• Sabbagh, Karl, The Riemann hypothesis, Farrar, Straus and Giroux, New York, 2003, ISBN 978-0-374-25007-2, MR 1979664 
• du Sautoy, Marcus, The music of the primes, HarperCollins Publishers, 2003 [2015-08-23], ISBN 978-0-06-621070-4, MR 2060134, （原始内容存档于2015-09-07） 

外部链接

• Hazewinkel, Michiel (编), Prime number, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 
• Caldwell, Chris, The Prime Pages at primes.utm.edu（页面存档备份，存于互联网档案馆）.
• Prime Numbers，In Our Time (BBC Radio 4)的《In Our Time》节目。
• An Introduction to Analytic Number Theory, by Ilan Vardi and Cyril Banderier（页面存档备份，存于互联网档案馆）
• Plus teacher and student package: prime numbers（页面存档备份，存于互联网档案馆） from Plus, the free online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge.
• 出现质数实验 （页面存档备份，存于互联网档案馆）
• 出现可以被整除的机率

质数产生器与计算器

• Prime Number Checker （页面存档备份，存于互联网档案馆） identifies the smallest prime factor of a number.
• Fast Online primality test with factorization（页面存档备份，存于互联网档案馆） makes use of the Elliptic Curve Method (up to thousand-digits numbers, requires Java).
• Huge database of prime numbers（页面存档备份，存于互联网档案馆）
• Prime Numbers up to 1 trillion （页面存档备份，存于互联网档案馆）
• 素数发生器和校验器 （页面存档备份，存于互联网档案馆）