数学史
| 此條目翻譯自其他語言維基百科,需要相關領域的編者協助校對翻譯。 |
| 科学史 |
|---|
 |
|
数学史的主要研究对象是历史上的数学发现,调查它们的起源,或更广义地说,数学史就是对过去的数学方法与数学符号的探究。
数学起源于人类早期的生产活动,为古中国六艺之一,亦被古希腊学者视为哲学之起点。數學最早用於人們計數、天文、度量甚至是貿易的需要。這些需要可以簡單地被概括為數學對結構、空間以及時間的研究;對結構的研究是從數字開始的,首先是從我們稱之為初等代數的——自然數和整數以及它們的算術關係式開始的。更深層次的研究是數論;對空間的研究則是從幾何學開始的,首先是歐幾里得幾何和類似於三維空間[註 1]的三角學。後來產生了非歐幾里得幾何,在相對論中扮演著重要角色。

在进入知识可以向全世界传播的现代社会以前,有记录的新数学发现仅仅在很少几个地区重见天日。目前最古老的数学文本是《普林顿 322》(古巴比伦,约公元前1900年[2]),《莱因德数学纸草书》(古埃及,约公元前2000年-1800年[3]),以及《莫斯科数学纸草书》(古埃及,约公元前1890年)。以上这些文本都涉及到了如今被称为毕达哥拉斯定理的概念,后者可能是继简单算术和几何后,最古老和最广泛传播的数学发现。
在公元前6世纪后,毕达哥拉斯将数学作为一门实证的学科进行研究,他创造了古希腊语单词μάθημα(mathema),意为“(被人们学习的)知识学问”[4]。希腊数学家在相当大的程度上改进了这些数学方法[註 2],并扩大了数学的主题[5]。中国数学做了早期贡献,包括引入了位值制系统[6][7]。如今大行于世的印度-阿拉伯数字系统和运算方法,很可能是在公元后1000年的印度逐渐演化,并被伊斯兰数学家通过花拉子米的著作将其传到了西方[8][9]。伊斯兰数学则将以上这些文明的数学做了进一步的发展贡献。许多古希腊和伊斯兰数学著作随后被翻译成了拉丁文,引领了中世纪欧洲更深入的数学发展[10]。
从16世纪文艺复兴时期的意大利开始,算术、初等代数及三角学等初等数学已大体完备。17世纪变数概念的产生使人们开始研究变化中的量与量的互相关系和图形间的互相变换。随着自然科学和技术的进一步发展,为研究数学基础而产生的集合论和数理逻辑等也开始慢慢发展。
从古代到中世纪,数学发展的历史时期都伴随着数个世纪的停滞,但从16世纪以来,新的数学发展伴随新的科学发展,让数学不断加速大步前进,直至今日。
史前数学[编辑]
數學有着久遠的歷史。它被認為起源於人類早期的生產活動; 中國古代的六艺之一就有「數」[11],數學一詞在西方有希腊语詞源μαθηματικός(mathematikós), 意思是“学问的基础”,源于μάθημα(máthema)(“科学,知识,学问”)。
数学的源头在数、量和形之中[12]。现代对动物认知的研究表明,这并不是人类特有的概念。这些概念是狩猎者-采集者社会中日常生活的一部分。在一些语言的词汇中,保留了“一”、“二”、“很多”的区别,但并没有大于二的数,这个事实支持了“数”的概念是随时间而演化的说法[12]。
史前的人類就已嘗試用自然的法則來衡量物質的多少、時間的長短等抽象的數量關係,如時間-日、季節和年。算術(加減乘除)也自然而然地產生了。古代的石碑亦證實了當時已有幾何的知識。
已知最古老的數學工具是發現於斯威士蘭萊邦博山的莱邦博骨,大約是公元前35,000年的遺物。它是一支狒狒的腓骨,上面被刻意切割出29個不同的缺口,使用計數婦女及跟踪婦女的月經週期。相似的史前遗物也在非洲和法國出土,大約有35,000至20,000年之久,都與量化時間有關。[13]。发现于尼罗河上源之一的爱德华湖西北岸伊香苟地区(位于刚果民主共和国东北部),或许有20000年甚至更久,则刻有三组一系列的条纹符号,每列和骨头等长。常见的解释是已知最早的质数序列[14],亦有认为是代表六个阴历月的纪录[15]。 学者彼得·魯德曼否认素数序列的解释,他认为素数的概念只能出现在除法之后,而他认定除法是在公元前1000年后才出现的,因此在公元500年以前,素数是不太可能被理解的。他写道,“一个计数符号之类的东西为什么要展示2的倍数,10到20之间的素数,和一些几乎是10的倍数,这是没人尝试解释过的”[16]。而根据学者亞歷山大·馬沙克的说法,这个骨头可能影响了随后埃及数学的发展。因为埃及算术就像这块骨头一样,也使用了2的倍数,然而,这也是有争议的[17]。
其他地區亦發現不同的史前記數系統,如符木或於印加帝國內用來儲存數據的奇普。
在幾何學方面,公元前五千年的古埃及前王朝時期即已出現用圖畫表示的幾何圖案。也有人声称,年代大約是公元前三千年的英格蘭和蘇格蘭地區的巨石文化遺址中,也發現了融入幾何觀念的設計,包括圓形、橢圓形和畢達哥拉斯三元數。[18]。然而上述发现也全部有争议,而目前最早的无争议之数学史料当前依然是来自古巴比伦和古埃及史后的。
從歷史時代的一開始,數學內的主要原理是為了做稅務和貿易等相關計算,為了了解數字間的關係,為了測量土地,以及為了預測天文事件而形成的。这些需要可以简单地被概括为数学对數量、结构、空间及时间方面的研究。
古巴比伦数学[编辑]

古巴比伦数学指从早期苏米尔到希腊化时期和几乎是基督教曙光这段时期[19],任何美索不达米亚(现伊拉克)人的数学。巴比伦的数学主要来自两个独立的时期:公元前2000年的最初的几百年(旧巴比伦时期)和公元前1000年的几个世纪(塞琉古帝国时期)[20]。之所以命名为巴比伦数学,是因为巴比伦是当时数学研究中的中心。接着,在阿拉伯帝国之后,美索不达米亚,特别是巴格达,则再次成为了阿拉伯数学研究的中心。
与稀少的埃及数学史料不同,我们对巴比伦数学的认识来自1850年以来挖掘出的超过400块的泥板[21]。这些泥板以楔形文字,在湿润的粘土上写成,随后用火炉或日照烘干。其中的一些泥板看起来是被批改過的作业[22]。
书面数学的最早证据可以追溯到最早在美索不达米亚建立文明的古代苏米尔人,他们在公元前3000年发明了一个复杂的计量法。在公元前2500年左右,苏米尔人在泥板上写下了乘法表,并开始涉及几何习题和除法的问题,最早的巴比伦数字也能追溯到这个时期[23]。
巴比伦数学是用60进制的计数系统写成的[21]。现代文明中的60秒是一分钟,60分钟是一小时,一个圆周是360(60x6)度,以及用“分”和“秒”来表示非整数的弧度,都是来自巴比伦的这套计数系统。之所以选择60进制,可能是因为60可以被2、3、4、5、6、10、12、15、20和30整除[21]。同时,不像埃及、希腊或罗马,古巴比伦人使用的是真正的位值制系统,左侧的数字代表较大的值,和现代的十进制系统非常相似[20]。巴比伦计数系统的强大之处在于,分数可以像整数一样方便的表示,而分数乘法和整数乘法没有区别,这也和现代计数系统相似[20]。巴比伦人的计数法要优于文艺复兴之前的任何一个文明[24],这套计数法的力量允许人们达到非凡计算能力和计算精确度。例如,巴比伦泥板YBC 7289将根号2计算到了(十进制)小数点后5位[24]。然而,巴比伦人缺乏类似十进制的小数点,因此要确认一个符号的进位,通常只能根据上下文来判断[20]。在塞琉古帝国时期,巴比伦人发明了零的符号,作为空数位的占位符,然而这只用在数字的中间[20],零没有出现在数字的末尾,因此巴比伦人发明了非常接近但并非真正的进位系统[20]。
巴比伦数学涵盖的其他领域包括分数、代数,二次和三次方程,以及不規則倒數近似值的计算[25]。表格则包括乘法表,以及求解线性、二次、三次方程的方法,这在当时是了不起的成就[26]。旧巴比伦时期的表格还包括了最早对毕达哥拉斯定理的表述[27]。然而,和埃及数学一样,巴比伦数学同样没有注意到近似解和确切解的区别,以及一个问题的可解性。更重要的是,没有数学证明和逻辑原则[22]。
古埃及数学[编辑]

古埃及数学是指用埃及文写成的数学。在希腊化时期之后,希腊文取代了埃及文成为埃及学者使用的语言。埃及的数学研究随后在阿拉伯帝国成为阿拉伯数学的一部分得以延续,而阿拉伯文此时则成为了埃及学者的书面语言。
最具代表性的埃及数学著作是莱因德数学纸草书,断定为公元前1650年写成,不过这很可能是一份于公元前2000-1800年的中埃及写成的更早文献的誊抄本[28]。这是一份写给学生的代数和几何教材,此外,还包括面积公式、乘法除法的计算方法和分数的知识,此外也有其它数学知识的证据[29],包括素数和合数,代数平均数、几何平均数以及调和平均数,对埃拉托斯特尼筛法和完美数理论的简单理解[30]。它同时也展示了如何求解一阶线性方程[31],以及代数和几何数列[32]。
另一个重要的埃及数学文献是莫斯科纸草书,同样来自中埃及时期,断代为公年前1890年[33]。 这份纸草书包括了我们今天的应用题,看上去是为了趣味。其中一个问题被认为是特别重要的,因为它给出了计算锥台面积的方法:“如果你知道一个截断的角锥,高为4,底边为4,顶边为2。你需要先计算4的平方,得16, 然后乘以4,得8。计算2的平方,得4。然后把16、8、4加起来,等于28。计算6的三分之一,等于2。将28翻倍,等于56。因此,答案是56,这就是正确的答案。”
最后,柏林纸草书6619(公元前1800年)显示了古埃及人懂得如何求解二次代数方程[34]。
古希腊数学[编辑]

古希腊数学指用希腊文写成,从泰勒斯以来(约公元前600年)到公元后529年雅典学院关闭这段时间的数学成果[35]。希腊数学家居住在整个东地中海,从意大利到北非的地带,但拥有相同的文化和语言。亚历山大大帝之后的希腊数学,有时也被称作希腊化数学[36]。
古希腊数学比其他的早期文明发展出的数学更加先进复杂。古希腊数学之前存留下来的记录都表明了归纳推理的应用,也就是通过重复的观察来建立经验法则。但希腊数学正相反,使用演绎推理。希腊人使用逻辑从定义和公理中推导出结论,并在数学上严谨地证明它们[37]。
古希腊数学被认为是源于泰勒斯(公元前624到546年)和毕达哥拉斯(公元前582到507年)。虽然他们的影响程度依然是有争议的,但他们或许受到了埃及和巴比伦数学的启发。根据传说,毕达哥拉斯曾前往埃及向祭司学习数学、几何以及天文学。

泰勒斯使用几何学来解决问题,例如计算金字塔的高度,以及船只到海岸的距离。他也被认为是将演绎推理应用到几何学的第一人。由于推导出了泰勒斯定理的四个推论,他被誉为是第一个真正的数学家,以及第一个有署名的数学发现[39]。毕达哥拉斯建立了毕达哥拉斯学院,它的原则是数学统治着宇宙,并有“万物皆数”的格言[40]。毕达哥拉斯是“数学”这个词语的提出者,也是因兴趣而研究数学的先驅。毕达哥拉斯猜想的最早证明就归功于毕达哥拉斯学派[41],尽管对整个定理的表述已经有很长时间的历史了。他们也证明了无理数的存在[42][43]。

柏拉图在数学史上因启发和指导他人而非常重要[44]。他创立的雅典柏拉图学园成为了公元4世纪时世界数学的中心,也是当时一流数学家的母校,比如欧多克索斯[45]。柏拉图也探讨了数学的基础[46],澄清了一些定义(例如直线是“不断延伸的长度”),并对前提做了重新整理[47]。数学分析的方法也同样归功于柏拉图,一个计算勾股数的公式就以他的名字命名[45]。
欧多克索斯(公元前408到355年)发展了穷竭法,是现代积分法的前身[48];应用了比例论避免了无限小数所遇到的问题[49]。前者使计算曲线图形的面积和体积成为可能[50],后者使后来的几何学家极大推动了几何学的发展。虽然他并没有具体的数学发现,但亚里士多德认为他是把数学建立在逻辑基础上的功臣[51]。
在公元前3世纪,数学教育和研究的中心在亚历山大港的缪斯神殿(后世也称为亚历山大博物馆)[52]。这是欧几里得讲课和写下《几何原本》的地方,后者被认为是历史上最成功和最具有影响力的教科书[1]。《几何原本》用公理化方法引入了数学的严谨性,并且其中最早的“定义”、“公理”、“定理”、“证明”的格式至今依然在数学中使用。尽管绝大多数《几何原本》中的内容都是已知的,但是欧几里得将他们组合成了条理分明的一套逻辑框架体系[53]。《几何原本》因在20世纪中期前教导了所有的西方人而闻名,其中的内容依然在今天的几何课上讲授[54]。除了欧几里得几何中令人熟悉的定理以外,《几何原本》还是当时所有的数学科目的入门课本,例如数论、代数和立体几何[53],包括了2的平方根是无理数,以及素数有无穷多个的证明。欧几里得的著作广泛,例如圆锥曲线、光学、球面几何学和力学,但只有一半得以保存下来[55]。

叙拉古的阿基米德一致被认为是古代最伟大的数学家[56],他使用了穷竭法求无穷级数的和,计算出了抛物线下的面积,这种方法在现代的微积分课堂上并不陌生[57]。他还显示了通过穷竭法可以将 的值计算到任何想要的精度,他还求得了在当时最為精确的 值:藉在 與 之间[58]。他还讲解了后世以他的名字命名的阿基米德螺线,发现了旋转曲面的面积公式(抛物面,椭球面和双曲面)[57],以及一个可以灵活表示极大数字的系统[59]。尽管他在物理和许多高级机械装置上的贡献也广为人知,但他本人更看中自己的数学原则和思想的价值。[60]。他认为自己最伟大的成就,是发现球形的表面积和体积公式,也就是证明了球外接圆锥的表面积和体积是该圆锥的 。[61]
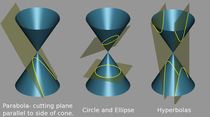
阿波罗尼奥斯最重大的贡献是研究圆锥曲线,表明了通过改变平面截断二次锥面的角度,可以获得全部三种圆锥曲线[62]。他创造了我们如今使用的三个术语:“抛物线”(英语:parabola,即齐曲线)、“椭圆”(英语:ellipse,即亏曲线)和“双曲线”(英语:hyperbola,即超曲线)[63]。他的《圆锥》是古代最著名和至今保存最完好的著作之一。在书中,他推出的许多定理随后被证明是数学家和研究行星运动的天文学家的无价之宝,例如艾萨克·牛顿[64]。虽然无论是阿波罗尼奥斯本人,还是其它的希腊数学家都没有迈入解析几何的领域,但阿波罗尼奥斯对某些椭圆曲线的处理方式已经和现代方法相似,他的一些著作也预示了1800年以后笛卡儿解析几何的出现[65]。

。
在大概在同一时间,埃拉托斯特尼发明了寻找素数的埃拉托斯特尼筛法[66]。公元前3世纪,通常认为是希腊数学的黄金时代,在此之后,就再也没有那么多纯数学的研究成果出现了[67]。尽管如此,这之后的应用数学得到的很大的发展,例如最有名的三角函数很大程度上是为了满足天文学的需要[67]。喜帕恰斯被认为是三角函数的创始人,他编制了第一张三角函数表,360度圆周的系统性应用也是自他开始[68] 。亚历山大的海伦被归功于发现通过三边计算三角形面积的海伦公式,也是认识到负数可能开平方的第一人[69]。亚历山大港的梅涅劳斯提出了梅涅劳斯定理,是球面几何的先驱[70]。古代最完整和最具影响力的三角函数著作是托勒密的《天文学大成》,这是天文学的里程碑著作,其中的三角函数表被随后的天文学家继续使用了一千年[71]。利用三角法求圆内接四边形边长的托勒密定理也归功于他本人,托勒密精确计算出了圆周率为 3.1416,这直到中世纪欧洲都是很精确的(中国除外)[72]。
在托勒密去世后一个死气沉沉的时段过去了,接下来的公元250到公元350年,有时被称为希腊数学的“白银时代”[73]。在这个时段,丢番图在代数,特别是不定分析(即“丢番图分析”)方面,也作出了令人瞩目的贡献[74]。如今,丢番图方程和丢番图逼近是一个重要的研究领域。丢番图的主要作品是《算术》,其中包括了150个代数问题,研究了方程,特别是不定方程的解析解[75]。《算术》对随后的数学家产生了巨大的影响,例如皮埃尔·德·费马就是在阅读《算术》时,尝试一般化其中的问题而想到了费马大定理[76]。丢番图对数学記号的贡献也很大,《算术》是目前已知第一个使用簡字代數系统及代数符号的文獻。[75]
帕普斯最後一位希臘的偉大數學家,他生活於約西元 4 世紀,主要的貢獻有帕普斯定理和古爾丁定理,後世還有以帕普斯命名的帕普斯構形和帕普斯圖。其著作《數學彙編》一書記錄了許多重要的古希臘數學成果,因為保存良好,在數學史上意義重大[77]。然而在帕普斯之後的數學家,不再有顯著的創新,大多數的工作內容都流於評論前人的發現。
第一位有历史记录的女数学家是希帕提娅。她继承了父亲的职位,成为大图书馆的馆长,并且写了很多关于应用数学的著作。因为亚里山大港的基督教社群认为她引起了一起政治纠纷,她便被撕去衣服,以尖锐的蚌壳(另一说是砖瓦)将她的肉从骨上刮下屠戮致死[78]。
中国数学[编辑]


早期中国数学和世界其它地方的数学有很大不同,因此可以合理认为是独立发展的[79]。现存最古老的中国数学文献是《周髀算经》,成书年代有很多说法,从公元前1200年到公元前100年都有,但认为是在公元前300年左右似乎是合理的[80]。
中国数学最特别的一点就是使用了十进制数位表示法,独特的“算筹数”用来表示从1到10的数字,而额外的算筹则被用来表示10的乘方[81]。因此,数字123可以表示为符号1,紧跟着符号100,接着符号2与符号10,最后符号3。这是当时全世界最先进的计数系统,而且在现代印度-阿拉伯数字系统引入之前,显然已经被使用了数个世纪[82]。算筹可以表示任意的大数,并且使得计算可以在中式算盘上进行。算盘的发明日期是不确定的,但最早的书面记录是在公元190年,东汉徐岳撰写的《数术记遗》中提到。
中国现存最古老的几何学作品来自《墨经》,由墨子的弟子编撰。《墨经》涉及了关于物理科学的很多领域的,也讲解了少量的几何定理[83]。
在公元前212年,秦始皇下令焚烧一切不被大秦帝国认可的书籍,史称焚书坑儒,尽管命令并没有被绝对遵守,但这导致了21世纪的我们对在此之前的中国数学不甚了解。在焚书之后的公元前212年,成书于汉朝的,被认为是扩展了数学的部分相关著作,如今也已遗失。在这类著作中,最重要的是《九章算术》,此书完整的标题首次出现在公元179年,但在这之前也有提到过部分。本书包括了246个应用题,包含了农业、商业、求塔的高度、工程学和测绘学,还包括了关于直角三角形的pi数值的内容[80]。它还证明了勾股定理,以及高斯消元的公式[來源請求]。刘徽在公元3世纪所作的注释中,给出了精确到小数点后5位的圆周率[84]。到了公元5世纪,祖冲之将π计算到了小数点后7位,他靠计算上的毅力[85][86],计算出之后1000年间最准确的π值[84]。他也发明了以祖暅原理的方法计算球的体积[87]。
中国数学的最高峰出现在13世纪宋朝,此时中国代数得到了发展。其中最重要的著作是朱世杰的《四元玉鉴》,研究一元高次方程组的解,后称为秦九韶算法,即后世欧洲的霍纳算法[84]。《四元玉鉴》中还包括了八次幂的帕斯卡三角,尽管早在公元1100年就曾出现在中国的数学著作中[88]。中国也发明了复杂的组合数学方面的图形,也就是幻方和幻圆,在古代就有记载,后被杨辉完善[88]。
就算到了文艺复兴之后,欧洲数学开始繁荣发展,欧洲和中国数学依然是完全独立的,而中国对外的数学思想传播在13世纪时开始下降。到16世纪和18世纪之间,耶稣会传教士利玛窦等人,交流了欧洲和中国的数学思想,尽管此时,传入的数学思想已经比传出的多了[88]。
印度数学[编辑]


印度次大陆上最早的文明是印度河流域文明,在公元前2600年到公元前1900年之间,在印度河畔繁荣发展。他们的城市布局是规则的几何图形,但没有留存下来的数学档案[89]。
印度-阿拉伯数字是印度的数学家发明的,他们曾经叫做“印度数字”,但后来被欧洲人称作“阿拉伯数字”,因为是阿拉伯商人把这种数字引入欧洲的[90]。
在印度-阿拉伯数字系统中,有许多用来表示数字的符号,全部都是从婆罗米数字演化而来的。大约十几种主要的印度手稿都有独特的数字符号(在仔细查阅Unicode字符表时就可发现)。下面的表格展示了两个例子:

现存最古老的印度记录有舒爾巴經(断代不同,在公元前8世纪到公元2世纪)[91],这是一份宗教著作的附录,包括了建设不同形状祭坛的简单规则,例如正方形、长方形、平行四边 形和其它图形[92]。和埃及相似,数学最初的祭坛应用指明了数学的起源之一是宗教仪式[91]。舒爾巴經还给出了构造和给定正方形面积(大致)相同的圆的方法,这隐含了对pi值不同精度的计算[93][94]。除此之外,他们还将2的平方根计算到了小数点后7位,列出了勾股数,并且说明了勾股定理[95]。而这一切成果都曾在古巴比伦数学中出现,表明了美索不达米亚文明的影响[91]。然而,目前还不清楚舒爾巴經是否影响了日后的印度数学。和中国一样,印度数学同样缺乏连续性,重大的突破往往伴随着长时间的死寂[91]。
波你尼(公元前5世纪)发明了梵语语法[96]。他的表示法很接近现代数学符号,并且应用了元规则、几何变换和递归[來源請求]。賓伽羅在他的诗歌韵律论述文中,使用了和二进制计数系统相关的文学手法[97][98]。他对音乐节拍的组合数学讨论,相当于二项式定理的简单版本;賓伽羅的著作还包括了斐波那契数列的基本思想(称作 mātrāmeru)[99]。
继舒爾巴經之后的下一份重要的数学档案是《蘇雅西德漢塔》曆數書,是公元4世纪到公元5世纪写成的天文学著作,显示了来自希腊的强烈影响[100]。它们之所以意义重大,是因为它是最早基于半弦来定义三角函数关系的,就像现代几何学一样,而非托勒密三角几何中的全弦[101]。尽管伴随着一系列翻译错误,但正弦(sine)和余弦(cosine)就是来自梵语的jiya和kojiya[101]。
在公元5世纪,阿耶波多完成了《阿里亚哈塔历书》,一本很薄的著作,用诗篇写成,目的是作为天文计算和数学测量法的补充,尽管其中并没有逻辑和演绎法的应用[102]。虽然书中几乎一半的内容都是错误的,但这是十进制进位系统第一次出现,几个世纪之后,阿拉伯数学家阿布·比鲁尼表示, 此书是“普通石头和高贵水晶的混合”[103]。
公元7世纪,婆罗摩笈多发现了婆罗摩笈多定理,婆罗摩笈多性质和婆罗摩笈多公式。并且首次《婆罗摩历算书》提出了零。他清晰的阐述了如何将零同时作为占位符和数字,并且解释了印度-阿拉伯数字系统[104]。 从这本印度著作的一本阿拉伯语翻译(约公元770年)中,阿拉伯数学家引进了此计数系统,并且将其转化为了阿拉伯数字。阿拉伯数学家又将这套数字系统的知识在12世纪带到了欧洲,并在此时取代了一切更老的数字。在公元10世纪,大力摩羅对賓伽羅著作的注释中,包括了对斐波那契数列和帕斯卡三角的研究,并提出了矩阵。[來源請求]
在公元12世纪,居住在印度南部的婆什迦罗第二[105]全面的写下了关于数学所有分支的著作。他的著作包含的数学概念等价或几乎等价于我们今天的无穷小量、导数、中值定理和正弦函数的导数。但他究竟在多大程度上提前发明了微积分,依然是一个在被数学史学家争议的论题[106]。

在14世纪,桑加馬格拉馬的馬德哈瓦, 喀拉拉数学学院的创立者,发现了π的莱布尼茨序列,并用该公式的21项计算出圆周率为3.14159265259。馬德哈瓦也发现了用来计算反正切的馬德哈瓦-格雷果里级数。馬德哈瓦-牛顿公式也给出的正弦和余弦函数的计算以及它们的泰勒逼近[107]。在16世纪,耶斯特迪瓦将学院的理论统一成了《數學闡明》[108]。然而,喀拉拉学院并没有发展出一套微分和积分的完整理论,也没有任何直接证据证明喀拉拉学院的成果曾被传出[109][110][111][112]。
阿拉伯数学[编辑]

横跨波斯、中东、中亚、北非、伊比利亚和印度部分地区的阿拉伯帝国在公元八世纪对数学做了重要贡献。尽管大多数阿拉伯著作都是用阿拉伯语写成的,但多数作者不是阿拉伯人,这就像是希腊语之于希腊化时期一样,阿拉伯语是当时整个伊斯兰世界非阿拉伯学者的书面语。
在九世纪,波斯数学家穆罕默德·伊本·穆薩·花拉子米写下了很多关于印度-阿拉伯数字和方程解法的重要书籍。他在公元825年写成的《印度数字的计算》,加上肯迪的著作,共同把印度数学和印度数字传入西方。Algorithm(算法)这个单词就是来自花拉子米名字的拉丁化拼写 Algoritmi;而 algebra(代数)这个单词则来自他的一本书,《消去与还原》(Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala)。他对根为整数的二次方程给出了详尽的代数解法[113],是为了代数本身而讲授初等形式代数的第一人[114]。他同时也讨论了两种解方程的基本方法,“消去”和“平衡”,也就是把方程一侧被减去的项,转移到方程的另一侧,从而将一侧的项“消去”了。花拉子米把这种方法称为 al-jabr[115]。他的代数学不再仅仅注重“给出的一系列问题,而是从基本术语开始讲解,给出所有可能出现的方程形式,从而明确了真正的研究对象”。他是为了方程本身而研究方程,他的研究是“在一般意义上的研究,不仅仅是为了解决一个问题,而是为了能通过它解决无限多个问题”[116]。
在埃及,阿布·卡米勒将代数推广到了无理数的集合,允许将平方根和四次方根作为二次方程的解和系数。他也发展出了解由含有三个未知数的三个方程联立组成的非线性方程组的解法。他成果中的一个独特之处,在于他试图在一些问题中,去寻找一切可能的解,他甚至对其中一个问题给出了2676个解[117]。他的著作成为了代数学发展的重要根基,并且影响了随后的数学家,如卡拉吉和斐波那契。
代数学的更深远发展是由卡拉吉在他的专著《哈法勒》中作出的。其中,他将数学方法进行了扩展来合併未知數的整數冪和整數根。在卡拉吉在公元1000年左右写成的一本书中,出现了一份很接近归纳法的数学证明,被用来证明二项式定理、帕斯卡三角形和立体积分求合的命题[118]。数学史学家弗朗茲·沃普克[119],赞扬卡拉吉是“引入代数微积分理论的第一人。”同样在公元10世纪,阿布·瓦法将丢番图的著作翻译成了阿拉伯语。海什木是第一个推导出四次幂和的公式的数学家,他使用的方法可以非常容易推广出能求任意次幂和的公式。他为了求抛物面面积而计算了积分,并且能够将他的结果推广到任何四次以内的多项式中。因此可以说,他差点就发现了计算多项式积分的通用公式,然而他并不关心高于四次的多项式[120]。
11世纪晚期,奧瑪·開儼写成了《欧几里得困难的讨论》,对欧几里得《几何原本》中他认为存在的缺陷进行了讨论,特别是关于平行公设的问题(即著名的第五公设)。他也是第一个发现了三次方程几何上的一般解,对历法改革也施加了重要的影响。[來源請求]
13世纪,納西爾丁·圖西推进了球面三角学的发展,他也写下了关于欧几里得平行公设具有影响力的著作。16世纪,吉亞斯丁·賈姆希德·麥斯歐德·阿爾-卡西将圆周率的值计算到了小数点后16位。卡西也提出了一个求n次方根的算法,他的这个算法是数个世纪后保羅·魯非尼和威廉·喬治·霍納提出的方法的一个特例。
阿拉伯数学家在同一时期的其它成就,包括了为阿拉伯数字加入了小数点,发现了除当时已被知晓正弦函数之外的全部现代三角函数;肯迪将密码分析和频率分析引入数学;海什木对解析几何的发展;奧瑪·開儼引领了代数几何的开端;卡爾·卡拉迪发明的一类代数符号[121]。
在奥斯曼帝国和十五世纪开始的萨非王朝期间,阿拉伯的数学发展陷入萧条之中。
中世纪欧洲数学[编辑]
中世纪欧洲,人们对数学产生兴趣的动机和如今的现代数学家大不相同。其中一个动因是,相信数学是理解神创造的自然秩序的钥匙 —— 这是常常被论证的主题,例如柏拉图在《蒂迈欧篇》中有所表示,而圣经(《所罗门智训》)则说 —— 神“处置一切事物,原有一定的尺度、数目和衡量。”[122]
波爱修斯在他的课程中为数学提供了一席之地,在公元6世纪,他创造了词汇四术(quadrivium)来指对算术、几何、天文学和音乐的学习。他著有《論算數》,是譯自希腊哲学家的尼科马库斯所写的《算术导论》。《音樂的綱要》同样也是源自希腊文献;以及对欧几里得《几何原本》的一系列摘录。他的著作都是理论而非实践的,而且在希腊和阿拉伯著作复原之前,一直都是数学研究的基础[123][124]。
12世纪,欧洲学者远游西班牙和西西里岛去搜集阿拉伯的科学文献,找到的文献包括花拉子米的《消去与还原》,被切斯特的羅伯特翻译成拉丁文;欧几里得《几何原本》的完整文本,被巴斯的阿德拉德、克恩頓州的赫爾曼和克雷莫纳的杰拉德翻译成了多个版本[125][126]。
这些新的著作点燃了数学复兴的星星之火。斐波那契首当其冲,在1202年写成并在1254年再版了《計算之書》,成为了继埃拉托斯特尼之后第一个做出重大发现的数学家,填补了这整整一千多年的空白。印度-阿拉伯数字相关的成果也被传入欧洲,并且其它相关的数学问题也有讨论。
14世纪,为了探究各种各样不同的数学问题,发展出了许多新的数学概念[127]。其中一个重要贡献是关于局部运动的数学发展。
托马斯·布拉德华提出,随着力(F)与阻力(R)的比例成几何增长,速度(V)就会成算术比例增长。布拉德华以一系列具体的例子来对此加以说明。虽然对数在当时还没有被发明出来,但我们可以把他的结论理解为 V = log(F/R)[128],虽然这是一个时代错误。布拉德华的分析,是肯迪和阿諾德·諾瓦两人研究量化复合药剂本质时所用的数学技巧,后来被转移到了另一个完全不同物理问题上的例子[129]。
14世纪牛津计算学者群的成员之一赫特斯柏立·威廉,以一种没有微积分和极限概念的形式,指出「一個均勻加速或均勻減速的物體在一段時間內所走過的(距離)與其均速在同一段時間所走過的(距離)相同」[130]。
赫特斯柏立和其它数学家,通过把一个物体全部的加速运动进行累计(今日即积分法),从而在数学上求得物体运动的距离,认为一个恒定运动的物体在加速或者减速运动时在一段时间内运动的距离等于相同时间内其以平均速度运动过的距离。[131]。
巴黎大学的尼克尔·奥里斯姆和意大利的喬瓦尼·迪·卡薩里独立的提出了(这个关系)的图示,断定一条表示均匀加速运动的直线,直线下面积就是物体运动的总路程[132]。在随后对欧几里得《几何原本》的注解中,奧里斯姆展示了一個物體在每一個連續的時間增量中會獲得一個與奇數數量成比例的增量。由於歐幾里德已經證明奇數數量的和是平方數,因此物體所獲得的總增量隨時間的平方增加。[133].
文艺复兴[编辑]

在文艺复兴期间,数学的发展和会计学的发展是相辅相成的[134]。虽然代数和记账之间并没有直接的联系,这门学科的教材和书籍也往往是为了给商人的孩子在算術学校或者算盤学校学习商业和贸易的实用技能而准备的。确实,如果只是记账的话大概是不需要代数的。但是,对于更复杂的交易,或者复息利率的计算,就必须掌握算术,而代数知识也就十分有用了。
皮耶罗·德拉·弗朗切斯卡(约1415-1492)著有关于立体几何与透视法的作品,包括《论绘画透视》,《论算术》和《论正则体》[135][136][137]。
卢卡·帕西奥利所著的《算术、几何、比例总论》在1494年于威尼斯首次印刷出版,其中包括了一篇27页的记账论文《计算和记录的细节》。这主要是编写和出售给商人将其作为参考书,给有兴趣的人作为娱乐破解其中数学谜题,以及教育他的儿子[138]。在《算术、几何、比例总论》中,帕西奥利首次在印刷书籍中引入了加号和减号,随后成为了意大利文艺复兴时期数学界的标准符号。《算术、几何、比例总论》也是已知的第一本在意大利印刷的代数书。不过,帕西奥利的不少思想是剽窃自皮耶罗·德拉·弗朗切斯卡的。
在16世纪上半叶的意大利,希皮奥内·德尔·费罗和尼科洛·塔尔塔利亚发现了三次方程的解法。吉罗拉莫·卡尔达诺在1545年发表的著作《大術》中,同时还记录了四次方程的一种解法,这是由他的学生洛多维科·费拉里发现的。在1572年,拉斐尔·邦贝利出版了他的著作《代数学》,这本书中,他解释了如何处理应用卡尔达诺公式解三次方程时可能会出现的虚数。
西蒙·斯蒂文的《十分之一》于1585年在荷兰首次发表,首次系统性讲解了十进制的处理方法,对随后所有关于实数系统的工作都有影响。
因为导航和大面积精确地图的需求驱动,三角几何学成长为数学的一个重大分支。巴塞洛繆·皮提斯卡斯首次使用了该词语,在1595年出版了《三角几何学》。雷吉奧蒙塔努斯的正弦和余弦函数表则在1533年出版[139]。
在文艺复兴期间,艺术家真实地表现自然世界的需求,与对希腊哲学的重新发现,引领着艺术家研究数学。艺术家们同时还是当时的工程师和建筑师,因此自然无论如何都要用到数学。绘画透视法的研究和相关的几何学发展是紧密相连的[140] 。
可见,到了16世纪,算术、初等代数、以及三角学等初等数学已大体完备。
科学革命期间的数学[编辑]
17世纪[编辑]

17世纪的欧洲涌现出了史无前例的数学和科学思潮。伽利略将一个从荷兰进口的玩具加以改进,制造了一部望远镜,用它观测到了环绕木星轨道运动的卫星。第谷·布拉赫则收集了天空中行星位置的巨量观测数据,而作为第谷的助理,约翰内斯·开普勒首次接触和认真研究了关于行星运动的主题。由于对数已经被当时的约翰·纳皮尔和约斯特·比尔吉发明出来,因此使开普勒的计算工作变得简单了。开普勒成功的建立了行星运动的数学法则[141]。同时,勒内·笛卡尔发展出了解析几何,因此行星的轨道就可以依照笛卡尔坐标系画出图像了。
在众多前人工作的基础之上,艾萨克·牛顿发现的物理定律解释了开普勒定律,牛顿汇集的许多数学概念就是今天的微积分。戈特弗里德·莱布尼茨,可以说是17世纪最重要的数学家,也独立地的发展出了微积分,他发明的很多微积分符号至今仍在使用着。科学和数学研究变成了一项国际活动,随后将很快遍及全球[142]。
除了研究天空的应用数学以外,应用数学伴随着皮埃尔·德·费马和布莱兹·帕斯卡的工作而开拓了新的领域。帕斯卡和费马奠定了概率论研究的基根,并对赌博游戏进行讨论而发展了相应的组合数学。帕斯卡还利用他最新研究出来的概率论提出了帕斯卡赌注。帕斯卡试图表明,皈依宗教的理由在于,尽管成功的概率很低,但得到的奖赏却是无限的。某种程度上,这预示了18到19世纪发展的功利主义的出现。
18世纪[编辑]

18世纪最具有影响力的数学家无疑是莱昂哈德·欧拉。他的贡献范围特别广泛,从因七桥问题创立图论,到标准化大量数学术语和符号都包括在内。比如说,他将负1 的平方根称为i,还推广了使用希腊字母 pi 来表述圆周率。他对拓扑学、图论、微积分、组合数学和复分析都做出了贡献,以此为证,众多的数学定理和记号都是以他的名字命名的。
其他18世纪重要的欧洲数学家,包括约瑟夫·拉格朗日,他在数论、代数、微积分和变分法方面做出了开拓性的贡献。拉普拉斯则在拿破仑时代做了举足轻重的工作,建立了天体力学和统计学的基础。
现代数学[编辑]
随着自然科学和技术的进一步发展,为研究数学基础而产生的集合论和数理逻辑等也开始慢慢发展。
19世纪[编辑]

在19世纪期间,数学的抽象程度显著增加了。卡尔·弗里德里希·高斯是这股浪潮的缩影。姑且不谈他对科学的贡献,他在复变函数、几何学和收敛级数上做出了革命性的工作。它也是给出代数基本定理和二次互反律令人满意的证明的第一人。

在这个世纪,发展出两种形式的非欧几里得几何,欧几里得的平行公设在这种几何中就不再成立了。俄罗斯数学家尼古拉·罗巴切夫斯基和他的竞争对手匈牙利数学家鲍耶·亚诺什,都独自的定义并研究了双曲几何。在双曲几何中,过一点可做的平行线不再是唯一了,而三角形的内角和小于180度。椭圆几何随后在19世纪由德国数学家波恩哈德·黎曼建立,在椭圆几何中,平行线一条也不能做了,而三角形的内角和大于180度。黎曼也将这三种几何学加以一般化并统一,发展出了黎曼几何。黎曼定义了“流形”的概念,从而将曲线和平面的概念推广了。
19世纪出现了抽象代数的伟大思想,德国的赫尔曼·格拉斯曼想出了最早的向量空间。爱尔兰的威廉·哈密顿则发展出了不遵循交换律的代数学。英国数学家乔治·布尔构想出了一种新的代数学,随后演化为了我们今天的布尔代数。布尔代数中只有0和1两种数值,是数理逻辑学的起点,并且在计算机科学中拥有众多重要应用。
奥古斯丁·路易·柯西、黎曼和卡尔·魏尔斯特拉斯则以在数学上更加严谨的形式重新表述了微积分。
同时,数学的局限性也第一次被发现了。挪威人尼尔斯·阿贝尔和法国人埃瓦里斯特·伽罗瓦证明了高于四次的多项式方程不存在通行的代数解法,也就是阿贝尔-鲁菲尼定理。其它19世纪的数学家应用了这个定理,从而证明了仅靠尺规作图将三等分任意角、将一个立方体扩大两倍,或者构造一个和正方形面积相等的圆,都是不可能的。而自古希腊以来数学家就在尝试解决这三个难题了。在另一方面,几何学仅有三维的局限性,因参数空间和超复数的提出而被克服了。
阿贝尔和伽罗瓦对多项式方程的解的研究,奠定了日后群论和抽象代数相关的发展基础。20世纪的物理学家和其他科学家发现群论是研究对称性的理想工具。
在19世纪晚期,格奥尔格·康托尔首次建立了集合论。集合论让人们可以严谨地表示极限的概念,并且随后成为了几乎所有数学家的通用语言。康托尔的集合论和数理逻辑在皮亚诺、鲁伊兹·布劳威尔、大卫·希尔伯特和伯特兰·罗素手中蒸蒸日上,也引发了关于数学基础的长时间争论。
在19世纪,大量的国家数学协会被建立起来,例如1865年伦敦数学协会、1872年法国数学协会、1884年意大利数学协会、1883年苏格兰数学协会,以及1888年的美国数学协会。而首个国际性的特别兴趣协会 —— 四元数协会 —— 在当时矢量等概念还存在争议的历史背景下,成立于1899年。
1897年,库尔特·亨泽尔引入了数论中的p进数概念。
20 世纪[编辑]

20世纪,数学开始成为一门主修专业。每年,成百上千人成为新的数学博士,而且数学家既可以留在学术界,又可以加入工业界。Klein百科全书则承担起了汇总整个数学和数学应用领域的任务。
在1900年国际数学家大会的演说中,大卫·希尔伯特列出了23个数学界的未解决问题。这些问题覆盖了许多不同的数学领域,随后成为了20世纪数学研究的中心。如今,10个问题已经解决,7个问题部分解决,而2个问题依然是开放的;还有4个问题由于太含糊,因此不能判断有没有解决。
此时,历史上有名的不少数学猜想也终获证明。1976年,沃夫冈·哈肯和凯尼斯·阿佩尔使用计算机证明了四色定理。安德鲁·怀尔斯在他人工作的基础上成功证明了费马大定理。保罗·寇恩和库尔特·哥德尔则证明了,连续性假设本身是独立于标准公理化集合论而存在的(也就是既不可能从中证明,也不可能从中反证)。在1998年,托马斯·黑尔斯证明了开普勒猜想。
此时,数学家们合作的规模与领域已经是空前的了。例如在1955年到1983年完成的有限 单群分类(即“宏伟定理”),其证明分散在由100多位作者发表的500多篇期刊论文中,完整的论文加起来共有10000多页;一组法国数学家,包括让·迪厄多内和安德烈·韦伊,使用笔名尼古拉·布尔巴基写作,尝试以最极端的严谨和泛化来加以表述全部的已知数学,他们的成果则是几十卷著作,然而这在数学教育上留下了有争议的影响。[143]

爱因斯坦在广义相对论中使用微分几何之后,微分几何也得到了一席之地;数学逻辑学、拓扑学,和冯·诺伊曼的博弈论等新的数学领域,则改变了通过数学方法可以 回答的问题类型;所有的数学结构全部通过公理而抽象化为了诸如度量空间、拓扑空间等概念;而数学家所作的这些抽象化工作本身的抽象化则引领人们通向范畴 论;亚历山大·格罗滕迪克和让-皮埃尔·塞尔则将用层论重新铸造了代数几何;而庞加莱自1890年开始的动态系统理论的定性研究终于也有了很大进展;在19世纪和20世纪之间,测度论被发展出来。测度论的应用包括了勒贝格积分,和安德雷·柯尔莫哥洛夫的公理化概率论,以及遍历论;纽结理论极大的扩展了;量子力学引领了泛函分析的发展;其它的新领域包括了洛朗·施瓦茨和分布论、不动点理论和奇点理论;勒内·托姆的突变论、模型论,以及本华·曼德博的分形;李论以及李群和李代数成为了一个主要研究领域。
亚伯拉罕·鲁滨逊引入了非标准分析,通过将实数域扩展到了包括无穷大和无穷小量的超实数域,从而平反了微积分中一时名声狼藉随后被极限理论取代的无穷小量方法;而约翰·何顿·康威发现了一个和组合博弈论有关,甚至比超实数更大的数字系统:超现实数。
而随着计算机的发展和不断进步,从最初的机械模拟计算机到随后的电子数字计算机,让工业界可以处理越来越大量的数据,来帮助规划大规模生产、配给和通讯,新的数学领域也因此发展出来:艾伦·图灵的可计算性理论、计算复杂性理论;德里克·亨利·莱默使用ENIAC促进了数论发展,提出卢卡斯-莱默检验法;克劳德·香农的信息论、信号处理、数据分析、最优化和其它运筹学的研究;在过去的世纪中,数学在很大程度上注重微积分和连续函数,但因为计算机和通讯网络的崛起,使离散概念也越发重要,还导致了组合数学,包括图论的扩张发展;数据处理速度和能力的提升,也让人们可以去研究那些过去需要大量时间进 行纸笔计算的数学问题,引出了数值分析和符号计算。而20世纪最重要的数学方法和算法包括:单纯形法、快速傅立叶变换、错误校验码、源自控制论的卡尔曼滤波,以及公钥密码学的RSA算法。
在同一时间,人们开始深入审视数学的极限。在1929年到1930年,数学家证明了,具有乘法或者加法其中之一的自然数系统之内的一切命题的真伪是可决定的,也就是可以通过某个算法自动计算出来。然而在1931年,库尔特·哥德尔发现,如果自然数同时包括乘法和加法,那么这个结论就不再成立了;同时包括乘法和加法的系统就是人们所知的皮亚诺算术,而这事实上是一个不完备的系统(仅靠皮亚诺算术就足够支撑数论了,包括可以表述素数)。而哥德尔的两个不完备定理表明,一个包括了皮亚诺算术的任何数学系统(涵盖了数学分析和几何的一切),真理永远凌驾于证明之上,即总会有在系统中不可能被证明的真命题。因此,数学本身不可能被规约为数学逻辑学,而大卫·希尔伯特企图将整个数学变得完备和一致的梦想也就此破灭而不得不改变了。

斯里尼瓦瑟·拉马努金是20世纪数学界最耀眼的身影之一,他是一位自学成才的印度数学家,猜想和证明了关于高合成数、整数分拆、渐进分析和仿θ函数的超过3000个定理,它也对伽马函数、模形式、发散级数、广义超几何函数和素数理论做了深入探索。
埃尔德什·保罗发表了有史以来最多的数学论文,并和上百名合作者一起工作。由于他的论文实在太多,以至于数学家提出了数学家版本的贝肯数:埃尔德什数,描述数学论文中一个作者与埃尔德什的“合作距离”的一种方式。
埃米·诺特则被许多人认为是数学史上最重要的女性[144]。她的研究包括环、域和域代数。
就像大部分研究领域一样,科学时代的信息爆炸导致了数学的专门化:在20世纪结束时,有超过上百种数学的专门领域,而数学学科分类标准则长达几十页[145]。越来越多的数学期刊开始出版,而到该世纪结束,因互联网的发展,又有了在线出版。
现代數學[编辑]
數學從古至今便一直不斷地延展,且與科學有豐富的相互作用,並使兩者都得到好處。數學在歷史上有著許多的發現,並且直至今日都還不斷地發現中。依據米哈伊爾·B·塞夫留克於美國數學會快報2006年1月的期刊中所說,「存在於數學評論資料庫中論文和書籍的數量自1940年(數學評論的創刊年份)現已超過了一百九十萬份,而且每年還增加超過七萬五千份的細目。此一學海的絕大部份為新的數學定理及其證明。」[146]
美國的克雷數學研究所在2000年時提出七個數學難題,稱為千禧年大獎難題,在2003年時俄羅斯數學家格里戈里·佩雷爾曼對龐加萊猜想的證明有決定性的貢獻[147],他也因此在同年獲得菲爾茲獎,但佩雷爾曼並未現身領獎,也不接受獎金,成为首位拒绝接受菲爾茲獎的数学家[148]。
二十一世紀時大部份的數學期刊除了印刷版外也會有網路的版本,而且有許多新的數學期刊只有網路版本,期刊开放获取的趨勢更加明顯,arXiv是期刊开放获取的一個重要網站。
数学的未来[编辑]
数学的许多发展趋势是可以观察到的,最明显的趋势就是这门学科变得越来越庞大,计算机变得越来越重要和强大,而数学在生物信息学上的应用领域日发扩大,而通过计算机分析的工业界和科学界数据则爆炸性增长。[來源請求]
注释[编辑]
参见[编辑]
參考資料[编辑]
- ^ 1.0 1.1 (Boyer 1991,"Euclid of Alexandria" p. 119)
- ^ J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277—318.
- ^ Neugebauer, Otto. The Exact Sciences in Antiquity 2. Dover Publications. 1969 [1957]. ISBN 978-0-486-22332-2. Chap. IV "Egyptian Mathematics and Astronomy", pp. 71–96.
- ^ Heath. A Manual of Greek Mathematics. : 5.
- ^ Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who first made mathematics a science."
- ^ George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics,Penguin Books, London, 1991, pp.140—148
- ^ Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, pp.428—437
- ^ Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
- ^ "The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." - Pierre Simon Laplace http://www-history.mcs.st-and.ac.uk/HistTopics/Indian_numerals.html (页面存档备份,存于互联网档案馆)
- ^ A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
- ^ 《周 礼·地官司徒·保氏》:「保氏掌谏王恶而养国子以道。乃教之六艺:一曰五礼,二曰六乐,三曰五射,四曰五驭,五曰六书,六曰九数。」东汉的郑玄在他的《周 礼注疏·地官司徒·保氏》中引郑司农(郑众)所言:「九数:方田、粟米、差分、少广、商功、均输、方程、赢不足、旁要,今有重差、夕桀、勾股也。」
- ^ 12.0 12.1 (Boyer 1991,"Origins" p. 3)
- ^ Mathematics in (central) Africa before colonization (PDF). [2016-05-02]. (原始内容 (PDF)存档于2012-02-07).
- ^ Williams, Scott W. The Oldest Mathematical Object is in Swaziland. Mathematicians of the African Diaspora. SUNY Buffalo mathematics department. 2005 [2006-05-06]. (原始内容存档于2015-03-25).
- ^ Marshack, Alexander (1991): The Roots of Civilization, Colonial Hill, Mount Kisco, NY.
- ^ Rudman, Peter Strom. How Mathematics Happened: The First 50,000 Years. Prometheus Books. 2007: 64. ISBN 978-1-59102-477-4.
- ^ Marshack, A. 1972. The Roots of Civilization: the Cognitive Beginning of Man’s First Art, Symbol and Notation. New York: McGraw-Hil
- ^ Thom, Alexander, and Archie Thom, 1988, "The metrology and geometry of Megalithic Man", pp 132-151 in C.L.N. Ruggles, ed., Records in Stone: Papers in memory of Alexander Thom. Cambridge University Press. ISBN 0-521-33381-4.
- ^ (Boyer 1991,"Mesopotamia" p. 24)
- ^ 20.0 20.1 20.2 20.3 20.4 20.5 (Boyer 1991,"Mesopotamia" p. 26)
- ^ 21.0 21.1 21.2 (Boyer 1991,"Mesopotamia" p. 25)
- ^ 22.0 22.1 (Boyer 1991,"Mesopotamia" p. 41)
- ^ Duncan J. Melville (2003). Third Millennium Chronology (页面存档备份,存于互联网档案馆), Third Millennium Mathematics. St. Lawrence University.
- ^ 24.0 24.1 (Boyer 1991,"Mesopotamia" p. 27)
- ^ Aaboe, Asger. Episodes from the Early History of Mathematics. New York: Random House. 1998: 30–31.
- ^ (Boyer 1991,"Mesopotamia" p. 33)
- ^ (Boyer 1991,"Mesopotamia" p. 39)
- ^ (Boyer 1991,"Egypt" p. 11)
- ^ Egyptian Unit Fractions (页面存档备份,存于互联网档案馆) at MathPages
- ^ ([//web.archive.org/web/20160401035240/http://mathpages.com/home/kmath340/kmath340.htm 页面存档备份,存于互联网档案馆) Egyptian Unit Fractions]
- ^ Egyptian Papyri. [2016-05-02]. (原始内容存档于2012-02-19).
- ^ Egyptian Algebra - Mathematicians of the African Diaspora. [2016-05-02]. (原始内容存档于2009-04-16).
- ^ (Boyer 1991,"Egypt" p. 19)
- ^ Egyptian Mathematical Papyri - Mathematicians of the African Diaspora. [2016-05-02]. (原始内容存档于2015-04-07).
- ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 99)
- ^ Martin Bernal, "Animadversions on the Origins of Western Science", pp. 72–83 in Michael H. Shank, ed., The Scientific Enterprise in Antiquity and the Middle Ages, (Chicago: University of Chicago Press) 2000, p. 75.
- ^ Bill Casselman. One of the Oldest Extant Diagrams from Euclid. University of British Columbia. [2008-09-26]. (原始内容存档于2012-06-04).
- ^ (Boyer 1991,"Ionia and the Pythagoreans" p. 43)
- ^ (Boyer 1991,"Ionia and the Pythagoreans" p. 49)
- ^ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.
- ^ Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum. The Annals of Mathematics. 1945.
- ^ James R. Choike. The Pentagram and the Discovery of an Irrational Number. The Two-Year College Mathematics Journal. 1980.
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 86)
- ^ 45.0 45.1 (Boyer 1991,"The Age of Plato and Aristotle" p. 88)
- ^ Calian, George F. One, Two, Three… A Discussion on the Generation of Numbers (PDF). New Europe College. 2014. (原始内容 (PDF)存档于2015-10-15).
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 87)
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 92)
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 93)
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 91)
- ^ (Boyer 1991,"The Age of Plato and Aristotle" p. 98)
- ^ (Boyer 1991,"Euclid of Alexandria" p. 100)
- ^ 53.0 53.1 (Boyer 1991,"Euclid of Alexandria" p. 104)
- ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0 p. 141: "No work, except The Bible, has been more widely used...."
- ^ (Boyer 1991,"Euclid of Alexandria" p. 102)
- ^ (Boyer 1991,"Archimedes of Syracuse" p. 120)
- ^ 57.0 57.1 (Boyer 1991,"Archimedes of Syracuse" p. 130)
- ^ (Boyer 1991,"Archimedes of Syracuse" p. 126)
- ^ (Boyer 1991,"Archimedes of Syracuse" p. 125)
- ^ (Boyer 1991,"Archimedes of Syracuse" p. 121)
- ^ (Boyer 1991,"Archimedes of Syracuse" p. 137)
- ^ (Boyer 1991,"Apollonius of Perga" p. 145)
- ^ (Boyer 1991,"Apollonius of Perga" p. 146)
- ^ (Boyer 1991,"Apollonius of Perga" p. 152)
- ^ (Boyer 1991,"Apollonius of Perga" p. 156)
- ^ (Boyer 1991,"Greek Trigonometry and Mensuration" p. 161)
- ^ 67.0 67.1 (Boyer 1991,"Greek Trigonometry and Mensuration" p. 175)
- ^ (Boyer 1991,"Greek Trigonometry and Mensuration" p. 162)
- ^ S.C. Roy. Complex numbers: lattice simulation and zeta function applications, p. 1 [1] (页面存档备份,存于互联网档案馆). Harwood Publishing, 2007, 131 pages. ISBN 1-904275-25-7
- ^ (Boyer 1991,"Greek Trigonometry and Mensuration" p. 163)
- ^ (Boyer 1991,"Greek Trigonometry and Mensuration" p. 164)
- ^ (Boyer 1991,"Greek Trigonometry and Mensuration" p. 168)
- ^ (Boyer 1991,"Revival and Decline of Greek Mathematics" p. 178)
- ^ (Boyer 1991,"Revival and Decline of Greek Mathematics" p. 180)
- ^ 75.0 75.1 (Boyer 1991,"Revival and Decline of Greek Mathematics" p. 181)
- ^ (Boyer 1991,"Revival and Decline of Greek Mathematics" p. 183)
- ^ (Boyer 1991,"Revival and Decline of Greek Mathematics" pp. 183–90)
- ^ Ecclesiastical History,Bk VI: Chap. 15. [2016-05-02]. (原始内容存档于2014-08-14).
- ^ (Boyer 1991,"China and India" p. 201)
- ^ 80.0 80.1 (Boyer 1991,"China and India" p. 196)
- ^ Katz 2007,第194–199頁
- ^ (Boyer 1991,"China and India" p. 198)
- ^ Needham, Joseph. Science and Civilisation in China. 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books Ltd. 1986.
- ^ 84.0 84.1 84.2 (Boyer 1991,"China and India" p. 202)
- ^ 清阮元撰《畴人传》:“后祖冲之更创密法,仍是割之又割耳,未能于徽注之外,别立新术也”
- ^ 吴文俊主编《中国数学史大系》第二卷 219页
- ^ Zill, Dennis G.; Wright, Scott; Wright, Warren S. Calculus: Early Transcendentals 3. Jones & Bartlett Learning. 2009: xxvii [2016-05-02]. ISBN 0-7637-5995-3. (原始内容存档于2016-05-03). Extract of page 27 (页面存档备份,存于互联网档案馆)
- ^ 88.0 88.1 88.2 (Boyer 1991,"China and India" p. 205)
- ^ (Boyer 1991,"China and India" p. 206)
- ^ Rowlett, Russ, Roman and "Arabic" Numerals, University of North Carolina at Chapel Hill, 2004-07-04 [2009-06-22], (原始内容存档于2018-07-31)
- ^ 91.0 91.1 91.2 91.3 (Boyer 1991,"China and India" p. 207)
- ^ T. K. Puttaswamy, "The Accomplishments of Ancient Indian Mathematicians", pp. 411–2, in Selin, Helaine; D'Ambrosio, Ubiratan (编). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. 2000. ISBN 1-4020-0260-2.
- ^ R. P. Kulkarni, "The Value of π known to Śulbasūtras 互联网档案馆的存檔,存档日期2012-02-06.", Indian Journal for the History of Science, 13 1 (1978): 32-41
- ^ J.J. Connor, E.F. Robertson. The Indian Sulba Sutras Univ. of St. Andrew, Scotland [2] (页面存档备份,存于互联网档案馆) The values for π are 4 x (13/15)2 (3.0044...), 25/8 (3.125), 900/289 (3.11418685...), 1156/361 (3.202216...), and 339/108 (3.1389).
- ^ J.J. Connor, E.F. Robertson. The Indian Sulba Sutras Univ. of St. Andrew, Scotland [3] (页面存档备份,存于互联网档案馆)
- ^ Bronkhorst, Johannes. Panini and Euclid: Reflections on Indian Geometry. Journal of Indian Philosophy (Springer Netherlands). 2001, 29 (1–2): 43–80. doi:10.1023/A:1017506118885.
- ^ Sanchez, Julio; Canton, Maria P. Microcontroller programming : the microchip PIC. Boca Raton, Florida: CRC Press. 2007: 37. ISBN 0-8493-7189-9.
- ^ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
- ^ Hall, Rachel W. Math for poets and drummers (PDF). Math Horizons. 2008, 15: 10–11 [2016-05-02]. (原始内容 (PDF)存档于2012-02-12).
- ^ (Boyer 1991,"China and India" p. 208)
- ^ 101.0 101.1 (Boyer 1991,"China and India" p. 209)
- ^ (Boyer 1991,"China and India" p. 210)
- ^ (Boyer 1991,"China and India" p. 211)
- ^ Boyer. The Arabic Hegemony. History of Mathematics. 1991: 226.
By 766 we learn that an astronomical-mathematical work, known to the Arabs as the Sindhind, was brought to Baghdad from India. It is generally thought that this was the Brahmasphuta Siddhanta, although it may have been the Surya Siddhanata. A few years later, perhaps about 775, this Siddhanata was translated into Arabic, and it was not long afterwards (ca. 780) that Ptolemy's astrological Tetrabiblos was translated into Arabic from the Greek.
- ^ Plofker 2009 182-207
- ^ Plofker 2009 pp 197 - 198; George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991 pp 298 - 300; Takao Hayashi, Indian Mathematics, pp 118 - 130 in Companion History of the History and Philosophy of the Mathematical Sciences, ed. I. Grattan.Guinness, Johns Hopkins University Press, Baltimore and London, 1994, p 126
- ^ Plofker 2009 pp 217 - 253
- ^ P. P. Divakaran, The first textbook of calculus: Yukti-bhāṣā, Journal of Indian Philosophy 35, 2007, pp 417 - 433.
- ^ Pingree, David, Hellenophilia versus the History of Science, Isis, December 1992, 83 (4): 562, JSTOR 234257, doi:10.1086/356288,
One example I can give you relates to the Indian Mādhava's demonstration, in about 1400 A.D., of the infinite power series of trigonometrical functions using geometrical and algebraic arguments. When this was first described in English by Charles Whish, in the 1830s, it was heralded as the Indians' discovery of the calculus. This claim and Mādhava's achievements were ignored by Western historians, presumably at first because they could not admit that an Indian discovered the calculus, but later because no one read anymore the Transactions of the Royal Asiatic Society, in which Whish's article was published. The matter resurfaced in the 1950s, and now we have the Sanskrit texts properly edited, and we understand the clever way that Mādhava derived the series without the calculus; but many historians still find it impossible to conceive of the problem and its solution in terms of anything other than the calculus and proclaim that the calculus is what Mādhava found. In this case the elegance and brilliance of Mādhava's mathematics are being distorted as they are buried under the current mathematical solution to a problem to which he discovered an alternate and powerful solution.
- ^ Bressoud, David, Was Calculus Invented in India?, College Mathematics Journal, 2002, 33 (1): 2–13, doi:10.2307/1558972
- ^ Plofker, Kim, The 'Error' in the Indian "Taylor Series Approximation" to the Sine, Historia Mathematica, November 2001, 28 (4): 293, doi:10.1006/hmat.2001.2331,
It is not unusual to encounter in discussions of Indian mathematics such assertions as that 'the concept of differentiation was understood [in India] from the time of Manjula (... in the 10th century)' [Joseph 1991, 300], or that 'we may consider Madhava to have been the founder of mathematical analysis' (Joseph 1991, 293), or that Bhaskara II may claim to be 'the precursor of Newton and Leibniz in the discovery of the principle of the differential calculus' (Bag 1979, 294).... The points of resemblance, particularly between early European calculus and the Keralese work on power series, have even inspired suggestions of a possible transmission of mathematical ideas from the Malabar coast in or after the 15th century to the Latin scholarly world (e.g., in (Bag 1979, 285)).... It should be borne in mind, however, that such an emphasis on the similarity of Sanskrit (or Malayalam) and Latin mathematics risks diminishing our ability fully to see and comprehend the former. To speak of the Indian 'discovery of the principle of the differential calculus' somewhat obscures the fact that Indian techniques for expressing changes in the Sine by means of the Cosine or vice versa, as in the examples we have seen, remained within that specific trigonometric context. The differential 'principle' was not generalized to arbitrary functions—in fact, the explicit notion of an arbitrary function, not to mention that of its derivative or an algorithm for taking the derivative, is irrelevant here
- ^ Katz, Victor J., Ideas of Calculus in Islam and India (PDF), Mathematics Magazine, June 1995, 68 (3): 163–174 [2016-05-02], JSTOR 2691411, doi:10.2307/2691411, (原始内容存档 (PDF)于2016-03-04)
- ^ (Boyer 1991,"The Arabic Hegemony" p. 230) "The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions."
- ^ Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, pp. 263–77: "In a sense, Khwarizmi is more entitled to be called "the father of algebra" than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers".
- ^ (Boyer 1991,"The Arabic Hegemony" p. 229) "It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" - that is, the cancellation of like terms on opposite sides of the equation."
- ^ Rashed, R.; Armstrong, Angela. The Development of Arabic Mathematics. Springer. 1994: 11–12. ISBN 0-7923-2565-6. OCLC 29181926.
- ^ Sesiano, Jacques. Abū Kāmil. Encyclopaedia of the history of science, technology, and medicine in non-western cultures. Springer: 4–5. 1997-07-31.
- ^ Victor J. Katz (1998). History of Mathematics: An Introduction, pp. 255–59. Addison-Wesley. ISBN 0-321-01618-1.
- ^ F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.
- ^ Katz, Victor J. Ideas of Calculus in Islam and India. Mathematics Magazine. 1995, 68 (3): 163–74. doi:10.2307/2691411.
- ^ 約翰·J·奧康納; 埃德蒙·F·羅伯遜, Abu'l Hasan ibn Ali al Qalasadi, MacTutor数学史档案 (英语)
- ^ 《智慧篇》, 11:20
- ^ Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", pp. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).
- ^ Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).
- ^ Marie-Thérèse d'Alverny, "Translations and Translators", pp. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
- ^ Guy Beaujouan, "The Transformation of the Quadrivium", pp. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
- ^ Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) ISBN 0-521-32260-X.
- ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 421–40.
- ^ Murdoch, John E. (1969) "Mathesis in Philosophiam Scholasticam Introducta: The Rise and Development of the Application of Mathematics in Fourteenth Century Philosophy and Theology", in Arts libéraux et philosophie au Moyen Âge (Montréal: Institut d'Études Médiévales), at pp. 224–27.
- ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 210, 214–15, 236.
- ^ Clagett, Marshall (1961) 中世纪数学科学 (Madison:Wisconsin 大学出版社), p. 284.
- ^ Clagett, Marshall (1961) 中世纪数学科学, (Madison: University of Wisconsin Press), pp. 332–45, 382–91.
- ^ Nicole Oresme, "Questions on the Geometry of Euclid" Q. 14, pp. 560–65, in Marshall Clagett, ed., Nicole Oresme and the Medieval Geometry of Qualities and Motions, (Madison: University of Wisconsin Press, 1968).
- ^ Heeffer, Albrecht: On the curious historical coincidence of algebra and double-entry bookkeeping, Foundations of the Formal Sciences, Ghent University, November 2009, p.7 [4] (页面存档备份,存于互联网档案馆)
- ^ della Francesca, Piero. De Prospectiva Pingendi, ed. G. Nicco Fasola, 2 vols., Florence (1942).
- ^ della Francesca, Piero. Trattato d'Abaco, ed. G. Arrighi, Pisa (1970).
- ^ della Francesca, Piero. L'opera "De corporibus regularibus" di Pietro Franceschi detto della Francesca usurpata da Fra Luca Pacioli, ed. G. Mancini, Rome, (1916).
- ^ Alan Sangster, Greg Stoner & Patricia McCarthy: "The market for Luca Pacioli’s Summa Arithmetica" (页面存档备份,存于互联网档案馆) (Accounting, Business & Financial History Conference, Cardiff, September 2007) p. 1–2
- ^ Grattan-Guinness, Ivor. The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. 1997. ISBN 0-393-32030-8.
- ^ Kline, Morris. Mathematics in Western Culture. Great Britain: Pelican. 1953: 150–151.
- ^ Struik, Dirk. A Concise History of Mathematics 3rd. Courier Dover Publications. 1987: 89. ISBN 9780486602554.
- ^ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0, p. 379, "...the concepts of calculus...(are) so far reaching and have exercised such an impact on the modern world that it is perhaps correct to say that without some knowledge of them a person today can scarcely claim to be well educated."
- ^ Maurice Mashaal, 2006. Bourbaki: A Secret Society of Mathematicians. American Mathematical Society. ISBN 0-8218-3967-5, ISBN 978-0-8218-3967-6.
- ^ Alexandrov, Pavel S., In Memory of Emmy Noether, Brewer, James W; Smith, Martha K (编), Emmy Noether: A Tribute to Her Life and Work, New York: Marcel Dekker: 99–111, 1981, ISBN 0-8247-1550-0.
- ^ Mathematics Subject Classification 2000 (PDF). [2016-05-02]. (原始内容存档 (PDF)于2016-03-04).
- ^ Sevryuk
- ^ Fields Medal-Grigory Perelman (PDF). [2013-11-30]. (原始内容存档 (PDF)于2012-11-03).
- ^ Maths genius declines top prize. BBC News. 22 August 2006 [16 June 2011]. (原始内容存档于2019-03-31).
外部連結[编辑]
- (中文)數學史--Episte Math (页面存档备份,存于互联网档案馆)