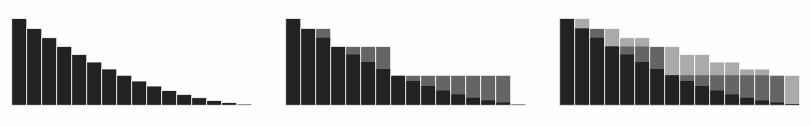柯西稠密判定法

  提示：此條目頁的主題不是柯西判別法。

在數學分析領域中、 柯西稠密測試（得名於法國數學家柯西），是一個應對無窮級數的收斂測試。

一般而言，一個單調遞減、非負的實數序列 $f(n)$所對應的級數$\displaystyle \sum \limits _{n=1}^{\infty }f(n)$收斂若且唯若其「凝結」級數（英語：Condensed Series）$\displaystyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})$ 收斂。 且此極限（如果存在）滿足以下不等式：

$0\ \leq \ \sum _{n=1}^{\infty }f(n)\ \leq \ \sum _{n=0}^{\infty }2^{n}f(2^{n})\ \leq \ 2\sum _{n=1}^{\infty }f(n)\ \leq \ +\infty$

換言之，「凝結」級數的極限在原級數極限和它的二倍之間。

推導

要證明該方法的正確性，我們需要證明上面的不等式。

$\sum _{n=1}^{\infty }f(n)\ \leq \ \sum _{n=0}^{\infty }2^{n}f(2^{n})\$

$\sum _{n=0}^{\infty }2^{n}f(2^{n})\ \leq \ 2\sum _{n=1}^{\infty }f(n)\$

第一個不等式可以通過替換原級數里的一些項得到。注意這裏需要用到原級數的性質（單調遞減）。

${\begin{array}{rcccccccl}\sum \limits _{n=1}^{\infty }f(n)&=&f(1)&+&f(2)+f(3)&+&f(4)+f(5)+f(6)+f(7)&+&\cdots \\&=&f(1)&+&{\Big (}f(2)+f(3){\Big )}&+&{\Big (}f(4)+f(5)+f(6)+f(7){\Big )}&+&\cdots \\&\leq &f(1)&+&{\Big (}f(2)+f(2){\Big )}&+&{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}&+&\cdots \\&=&f(1)&+&2f(2)&+&4f(4)&+&\cdots =\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})\end{array}}$

相似地，第二個不等式也需要我們重新組合和替換。

${\begin{array}{rcl}\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})&=&f(1)+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}+\cdots \\&=&{\Big (}f(1)+f(2){\Big )}+{\Big (}f(2)+f(4)+f(4)+f(4){\Big )}+\cdots \\&\leq &{\Big (}f(1)+f(1){\Big )}+{\Big (}f(2)+f(2)+f(3)+f(3){\Big )}+\cdots =2\sum \limits _{n=1}^{\infty }f(n)\end{array}}$

註釋

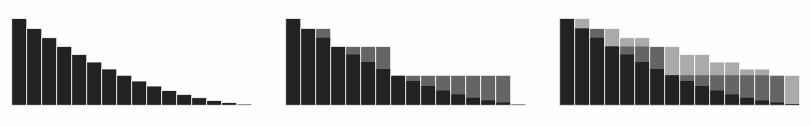
• Bonar, Khoury (2006). Real Infinite Series. Mathematical Association of America. ISBN 0-88385-745-6.

外部連結

• Cauchy condensation test proof （頁面存檔備份，存於互聯網檔案館）