中值定理

  提示：此條目頁的主題不是中間值定理。

在數學分析中，中值定理（英語：mean value theorem）大致是講，給定平面上固定兩端點的可微曲線，則這曲線在這兩端點間至少有一點，在這點該曲線的切線的斜率等於兩端點連結起來的直線的斜率。

更仔細點講，假設函數 $f$ 在閉區間 $[a,b]$ 連續且在開區間 $(a,b)$ 可微，則存在一點$c,\,a<c<b$，使得

$$f'(c)={\frac {f(b)-f(a)}{b-a}}$$

中值定理包括微分中值定理和積分中值定理。

微分中值定理

微分中值定理分為羅爾中值定理、拉格朗日中值定理和柯西中值定理，內容粗略的說是指平面上一段固定端點的可微曲線，兩端點之中必然有一點，它的斜率與連接兩端點的直線斜率相同（嚴格的數學表達參見下文）。

當提到中值定理時在沒有特別說明下一般指拉格朗日中值定理。

羅爾中值定理

羅爾定理的幾何意義

主條目：羅爾定理

如果函數$f(x)$滿足

1. 在閉區間$[a,b]$上連續；
2. 在開區間$(a,b)$內可導；
3. 在區間端點處的函數值相等，即$f(a)=f(b)$，

那麼在$(a,b)$內至少有一點$\xi (a<\xi <b)$，使得$$f^{\prime }(\xi )=0$$

這個定理稱為羅爾定理。

拉格朗日中值定理（中值定理）

拉格朗日中值定理的幾何意義

主條目：拉格朗日中值定理

令$f:[a,b]\rightarrow \mathbf {R}$為閉區間$[a,b]$上的一個連續函數，且在開區間$(a,b)$內可導，其中$a<b$。那麼在$(a,b)$上存在某個$c$使得

$$f'(c)={\frac {f(b)-f(a)}{b-a}}$$

此定理稱為拉格朗日中值定理，也簡稱中值定理，是羅爾中值定理的更一般的形式，同時也是柯西中值定理的特殊情形。

這個定理在可以稍微推廣一點。只需假設 $f:[a,b]\rightarrow \mathbb {R}$ 在 $[a,b]$ 連續，且在開區間 $(a,b)$ 內對任意一點 $x$，極限

$$\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$$

存在，為一個有限數字或者等於+∞或−∞.如果有限，則極限等於$f'(x)$。這版本定理應用的一個例子是函數 $x\to x^{1/3}$，實值三次方根函數，其導數在原點趨於無窮。

注意若一個可微函數的值域是複數而不是實數，則上面這定理就未必正確。例如，對實數 $x$ 定義$f(x)=e^{ix}$。那麼

$f(2\pi )-f(0)=0\neq f'(c)(2\pi -0)$

因$|f'(x)|=1\neq 0$ 時，$c$ 為開區間 $(0,2\pi )$ 中任意一點。

柯西中值定理

主條目：柯西中值定理

柯西中值定理，也叫拓展中值定理，是中值定理的一般形式，其敘述為：如果函數 $f$ 和 $g$ 都在閉區間$[a,b]$ 上連續，且在開區間 $(a,b)$ 上可導，那麼存在某個$c\in (a,b)$，使得

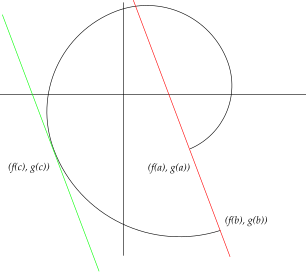柯西定理的幾何意義

$$(f(b)-f(a))g\,'(c)=(g(b)-g(a))f\,'(c)\,$$

當然，如果$g(a)\neq g(b)$ 且 $g(c)\neq 0$，則可表示成：

$${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}$$

在幾何上，這表示曲線 $${\begin{cases}[a,b]\to \mathbb {R} ^{2}\\t\mapsto (f(t),g(t))\end{cases}}$$ 上存在一點其切線平行於由兩點（$f(a),g(a)$）和（$f(b),g(b)$）所連接的直線。但柯西定理不能表明在任何情況下這種切線都存在，因為可能存在一些$c$值使$f(c)=g(c)=0$，所以在這些點曲線根本沒有切線。下面是這種情形的一個例子

$$t\mapsto (t^{3},1-t^{2})$$

在區間$[-1,1]$上，曲線由$(-1,0)$到$\left(1,0\right)$，卻並無一個水平切線，但在$t=0$處有一個駐點（實際上是一個尖點）。

柯西中值定理可以用來證明洛必達法則。拉格朗日中值定理是柯西中值定理當$g(t)=t$時的特殊情況。

積分中值定理

積分中值定理分為積分第一中值定理和積分第二中值定理，它們各包含兩個公式。其退化狀態均指在ξ的變化過程中存在一個時刻使兩個圖形的面積相等（嚴格表述在下面）。

積分第一中值定理

設$f:[a,b]\rightarrow \mathbb {R}$為一連續函數，$g:[a,b]\rightarrow \mathbb {R}$要求$g(x)$是可積函數且在積分區間不變號，那麼存在一點$\xi \in (a,b)$使得

$\int _{a}^{b}f(x)g(x)\,dx=f(\xi )\int _{a}^{b}g(x)\,dx$。

證明

在不失去一般性的條件下，設對所有$x$，有$g(x)\geq 0$； 因為$f$是閉區間上的連續函數，$f$取得最大值$M$和最小值$m$。於是 $mg(x)\leq f(x)g(x)\leq Mg(x)$

對不等式求積分，我們有 $m\int _{a}^{b}g(x)\,dx\leq \int _{a}^{b}f(x)g(x)\,dx\leq M\int _{a}^{b}g(x)\,dx$。 若$\int _{a}^{b}g(x)\,dx=0$，則$\int _{a}^{b}f(x)g(x)\,dx=0$。$\xi$可取$[a,b]$上任一點。

若不等於零那麼$\int _{a}^{b}g(x)\,dx>0$， $$m\leq {\frac {\int _{a}^{b}f(x)g(x)\,dx}{\int _{a}^{b}g(x)\,dx}}\leq M$$ 因為$m\leq f(x)\leq M$是連續函數，根據中間值定理，則必存在一點$\xi \in [a,b]$，使得 $f(\xi )={\frac {\int _{a}^{b}f(x)g(x)\,dx}{\int _{a}^{b}g(x)\,dx}}$

$g(x)<0$的情況按同樣方法證明。

積分第一中值定理推論的幾何意義

推論（拉格朗日中值定理的積分形式）

在上式中令$g(x)=1$，則可得出：

設$f:[a,b]\rightarrow \mathbf {R}$為一連續函數，則∃$\xi \in [a,b]$，使

$$f(\xi )={\frac {\int _{a}^{b}f(x)\,dx}{b-a}}$$

它也可以由拉格朗日中值定理推出：

設$F(x)$在$[a,b]$上可導，$f(x)=F^{\prime }(x)$，則∃$\xi \in [a,b]$，使

$$f(\xi )=F^{\prime }(\xi )={\frac {F(b)-F(a)}{b-a}}={\frac {\int _{a}^{b}f(x)\,dx}{b-a}}$$

積分第二中值定理

積分第二中值定理與積分第一中值定理相互獨立，卻又是更精細的積分中值定理。它可以用來證明Dirichlet-Abel反常Riemann積分判別法。

內容

若$f,g$在$[a,b]$上黎曼可積且$f(x)$在$[a,b]$上單調，則存在$[a,b]$上的點ξ使 $$\int _{a}^{b}{f(x)g(x)\mathrm {d} x=}f(a)\int _{a}^{\xi }{g(x)\mathrm {d} x+}f(b)\int _{\xi }^{b}{g(x)\mathrm {d} x}$$

退化態的幾何意義

第二積分中值定理退化形式的幾何意義

令$g(x)=1$，則原公式可化為： $\int _{a}^{b}{f(x)dx}=f(a)(\xi -a)+f(b)(b-\xi )$ 進而導出： $$\int _{a}^{\xi }{f(x)dx}-f(a)(\xi -a)=f(b)(b-\xi )-\int _{\xi }^{b}{f(x)dx}$$

此時易得其幾何意義為： 能找到ξ∈[a,b]，使得S[紅]+S[藍]=S[陰影]，即S[I]=S[II]

應用

關於積分中值定理的一個重要應用是可以去除掉積分號，或者使複雜的被積函數化為相對簡單的被積函數，從而使問題簡化。

參見

• 羅爾定理
• 柯西中值定理
• 中間值定理
• 極值定理