夹挤定理(英语:squeeze theorem),又称夹逼定理、夹极限定理、三明治定理、逼近定理、迫敛定理,是有关函数的极限的数学定理。指出若有两个函数在某点的极限相同,且有第三个函数的值在这两个函数之间,则第三个函数在该点的极限也相同[1]。
设 为包含某点
为包含某点 的区间,
的区间, 为定义在
为定义在 上,可能不包含a点的函数。若对于所有属于
上,可能不包含a点的函数。若对于所有属于 而不等于
而不等于 的
的 ,有:
,有:


则 。
。
 和
和 分别称为
分别称为 的下界和上界。
的下界和上界。
 若在
若在 的端点,上面的极限是左极限或右极限。
对于
的端点,上面的极限是左极限或右极限。
对于 ,这个定理还是可用的。
,这个定理还是可用的。
对于  ,
,
在任何包含0的区间上,除了 ,
, 均有定义。
均有定义。
对于实数值,正弦函数的绝对值不大于1,因此 的绝对值也不大于
的绝对值也不大于 。设
。设 ,
,  :
:



 ,根据夹挤定理
,根据夹挤定理
 。
。
对于  ,
,
首先用几何方法证明:若 ,
, 。
。
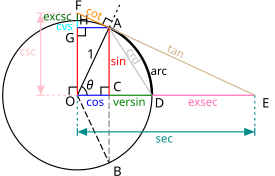
称(1,0)为D。A是单位圆圆周右上部分的一点。 在
在 上,使得
上,使得 垂直
垂直 。过
。过 作单位圆的切线,与
作单位圆的切线,与 的延长线交于
的延长线交于 。
。
由定义可得 ,
, 。
。






因为 ,根据夹挤定理
,根据夹挤定理
 。
。
另一边的极限可用这个结果求出。
高斯函数的积分的应用包括连续傅立叶变换和正交化。
一般高斯函数的积分是 ,现在要求的是
,现在要求的是 。
。
被积函数对于y轴是对称的,因此 是被积函数对于所有实数的积分的一半。
是被积函数对于所有实数的积分的一半。
![{\displaystyle (2I)^{2}=\left[2\int _{0}^{a}e^{-x^{2}}dx\right]^{2}=\left[\int _{-a}^{a}e^{-x^{2}}dx\right]^{2}=\int _{-a}^{a}\int _{-a}^{a}e^{-(x^{2}+y^{2})}dxdy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8400d2664e10ca7ecfa09db3a8dd4f83016c7792)
这个二重积分在一个 的正方形内。它比其内切圆大,比外接圆小。这些可用极坐标表示:
的正方形内。它比其内切圆大,比外接圆小。这些可用极坐标表示:


![{\displaystyle \lim _{a\to \infty }\pi \left(1-e^{-a^{2}}\right)=\lim _{a\to \infty }\pi \left(1-e^{-2a^{2}}\right)=\pi \vdash [2I(\infty )]^{2}=\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe163152aa218d8b76ea263f3a313a397f1d3dd)


若 ,
, ,而且
,而且 。
。
设 ,根据函数的极限的定义,存在
,根据函数的极限的定义,存在 使得:若
使得:若 ,则
,则 。
。
由于
 ,故
,故 。
。
若  ,则
,则 。于是,
。于是, 。
。


当 :
:

- 根据上面已证的特殊情况,可知
 。
。
![{\displaystyle f(x)=[f(x)-g(x)]+g(x)\to 0+L=L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/327451a1bc4604931a5a1cbe7474981301874ed3) 。
。
- ^ Stewart, James. Chapter 15.2 Limits and Continuity. Multivariable Calculus (6th ed.). 2008: 909–910. ISBN 978-0495011637.













































![{\displaystyle (2I)^{2}=\left[2\int _{0}^{a}e^{-x^{2}}dx\right]^{2}=\left[\int _{-a}^{a}e^{-x^{2}}dx\right]^{2}=\int _{-a}^{a}\int _{-a}^{a}e^{-(x^{2}+y^{2})}dxdy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8400d2664e10ca7ecfa09db3a8dd4f83016c7792)



![{\displaystyle \lim _{a\to \infty }\pi \left(1-e^{-a^{2}}\right)=\lim _{a\to \infty }\pi \left(1-e^{-2a^{2}}\right)=\pi \vdash [2I(\infty )]^{2}=\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfe163152aa218d8b76ea263f3a313a397f1d3dd)

















![{\displaystyle f(x)=[f(x)-g(x)]+g(x)\to 0+L=L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/327451a1bc4604931a5a1cbe7474981301874ed3)