Γ函數

Γ函數在實數定義域上的函數圖形

在數學中，$\Gamma \,$函數（伽瑪函數；Gamma函數），是階乘函數在實數與複數域上的擴展。如果$n$為正整數，則：

$\Gamma (n)=(n-1)!$

根據解析延拓原理，伽瑪函數可以定義在除去非正整數的整個複數域上：

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}{\rm {{d}t,}}$ $\Re (z)>0.$

數學家勒讓德首次使用了希臘字母Γ作為該函數的記號。在概率論和組合數學中此函數很常用。

定義

$\Gamma \,$函數可以通過尤拉（Euler）第二類積分定義：

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}{\rm {{d}t}}$

對複數$z\,$，我們要求$\mathrm {Re} (z)>0$。

$\Gamma$函數還可以通過對$\mathrm {e} ^{-t}\,$做泰勒展開，解析延拓到整個複數平面： $\Gamma (z)=\int _{1}^{\infty }{\frac {t^{z-1}}{\mathrm {e} ^{t}}}{\rm {d}}t+\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}{\frac {1}{n+z}}$

這樣定義的$\Gamma$函數在全平面除了$z=0,-1,-2,\ldots$以外的地方解析。

$\Gamma$函數也可以用無窮乘積的方式表示：

$\Gamma (z)={\frac {1}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}\left(1+{\frac {1}{n}}\right)^{z}$

這說明$\Gamma (z)$是亞純函數，而${\frac {1}{\Gamma (z)}}$是全純函數。

歷史動機

Γ函數本身可以被看作是一個下列插值問題的解：

『找到一個光滑曲線連接那些由 $y=(x-1)!$ 所給定的點$(x,y)$，並要求$x$要為正整數』

由前幾個的階乘清楚地表明這樣的曲線是可以被畫出來的，但是我們更希望有一個精確的公式去描述這個曲線，並讓階乘的操作不會依賴於$x$值的大小。而最簡單的階乘公式 $x!=1\times 2\times \cdots \times x$ 不能直接應用在應用在$x$值為分數的時候，因為它被限定在$x$值為正整數而已。相對而言，並不存在一個有限的關於加總、乘積、冪次、指數函數或是對數函數可以表達 $x!$，但是是有一個普遍的公式藉由微積分的積分與極限去表達階乘的，而 Γ函數就是那個公式。

階乘有無限多種的連續擴張方式將定義體擴張到非整數：可以通過任何一組孤立點畫出無限多的曲線。Γ函數是實務上最好的一個選擇，因為是解析的(除了正整數點)，而且它可以被定義成很多種等價形式。然而，它並不是唯一一個擴張階乘意義的解析函數，只要給予任何解析函數，其在正整數上為零，像是 $k\sin(m\pi x)$，會給出其他函數有着階乘性質。

無窮乘積

$\Gamma \,$函數可以用無窮乘積表示：

$\Gamma (z)=\lim _{n\to {\infty }}n!\;n^{z}\prod _{k=0}^{n}(z+k)^{-1}$

$\Gamma (z)={\frac {\mathrm {e} ^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}\mathrm {e} ^{\frac {z}{n}}$

其中$\gamma \,$是尤拉-馬歇羅尼常數。

Γ積分

$1=\int _{0}^{\infty }{\frac {x^{\alpha -1}\lambda ^{\alpha }\mathrm {e} ^{-\lambda x}}{\Gamma \left(\alpha \right)}}{\rm {d}}x$

$\implies {\frac {\Gamma \left(\alpha \right)}{\lambda ^{\alpha }}}=\int _{0}^{\infty }x^{\alpha -1}\mathrm {e} ^{-\lambda x}{\rm {d}}x$

遞迴公式

$\Gamma \,$函數的遞迴公式為： $\Gamma (x+1)=x\Gamma (x)$，

對於正整數$n\,$，有

$\Gamma (n+1)=n!$，

可以說$\Gamma \,$函數是階乘的推廣。

遞迴公式的推導

$\Gamma (n+1)=\int _{0}^{\infty }\mathrm {e} ^{-x}x^{n+1-1}\mathrm {d} x=\int _{0}^{\infty }\mathrm {e} ^{-x}x^{n}{\rm {d}}x$

我們用分部積分法來計算這個積分：

$\int _{0}^{\infty }\mathrm {e} ^{-x}x^{n}\mathrm {d} x=\left[{\frac {-x^{n}}{\mathrm {e} ^{x}}}\right]_{0}^{\infty }+n\int _{0}^{\infty }\mathrm {e} ^{-x}x^{n-1}{\rm {d}}x$

當$x=0\,$時，${\tfrac {-0^{n}}{\mathrm {e} ^{0}}}={\tfrac {0}{1}}=0$。當$x\,$趨於無窮大時，根據洛必達法則，有：

$\lim _{x\rightarrow \infty }{\frac {-x^{n}}{\mathrm {e} ^{x}}}=\lim _{x\rightarrow \infty }{\frac {-n!\cdot 0}{\mathrm {e} ^{x}}}=0$.

因此第一項$\left[{\tfrac {-x^{n}}{\mathrm {e} ^{x}}}\right]_{0}^{\infty }$變成了零，所以：

$\Gamma (n+1)=n\int _{0}^{\infty }{\frac {x^{n-1}}{\mathrm {e} ^{x}}}{\rm {d}}x$

等式的右面正好是$n\Gamma (n)\,$, 因此，遞迴公式為：

${\Gamma (n+1)=n\Gamma (n)}\,$.

重要性質

• 當$z\to 0^{+}$時，$\Gamma (z)\to +\infty$
• 歐拉反射公式（余元公式）：

$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin {\pi z}}}\quad (0<\mathrm {Re} (z)<1)$.

由此可知當$\ z={\tfrac {1}{2}}$時，$\Gamma \left({\tfrac {1}{2}}\right)={\sqrt {\pi }}$.

• 伽馬函數還是負自然指數函數的梅林轉換: $\Gamma (z)={\mathcal {M}}\{e^{-x}\}(z).$

• 乘法定理：

$\Gamma (z)\;\Gamma \left(z+{\tfrac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z)$。

$\Gamma (z)\;\Gamma \left(z+{\tfrac {1}{m}}\right)\;\Gamma \left(z+{\tfrac {2}{m}}\right)\cdots \Gamma \left(z+{\tfrac {m-1}{m}}\right)=(2\pi )^{\frac {m-1}{2}}\;m^{{\frac {1}{2}}-mz}\;\Gamma (mz)$.

• 此外：

$\Gamma \left(n+{\tfrac {1}{2}}\right)={\frac {(2n)!{\sqrt {\pi }}}{n!4^{n}}}$.

• 使用乘法定理推導的關係：

$\Gamma (1/6)=\Gamma (1/3)^{2}/{\sqrt {\pi }}*2^{2/3}*\sin({\pi /3}).$

$\Gamma (5/6)=1/\Gamma (1/3)^{2}*{\sqrt {\pi }}^{3}*2^{4/3}/{\sqrt {3}}.$

$\Gamma (1/10)=\Gamma (1/5)*\Gamma (2/5)/{\sqrt {\pi }}*2^{4/5}*\sin({2*\pi /5}).$

$\Gamma (3/10)=\Gamma (1/5)/\Gamma (2/5)*{\sqrt {\pi }}/2^{3/5}/\sin({3*\pi /10}).$

$\Gamma (7/10)=\Gamma (2/5)/\Gamma (1/5)*{\sqrt {\pi }}*2^{3/5}.$

$\Gamma (9/10)=1/(\Gamma (1/5)*\Gamma (2/5))*{\sqrt {\pi }}^{3}/2^{4/5}/(\sin(\pi /10)*\sin({2*\pi /5})).$

此式可用來協助計算t分佈概率密度函數、卡方分佈概率密度函數、F分佈概率密度函數等的累計概率。

• 極限性質

對任何實數α

$\lim _{n\to \infty }{\frac {\Gamma (n+\alpha )}{\Gamma (n)n^{\alpha }}}=1,\qquad \alpha \in \mathbf {R}$

斯特靈公式

Γ函數與斯特靈公式

$\Gamma (z+1)$（藍色）、${\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}$（橘色），數字越大${\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z},$會越趨近$\Gamma (z+1)$。但${\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}$會在負值則會因為出現虛數而無法使用。

主條目：斯特靈公式

斯特靈公式能用以估計$\Gamma (z)$函數的增長速度。公式為：

$\Gamma (z+1)\sim {\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z},$

其中e約等於2.718281828459。

特殊值

${\begin{array}{rcccl}\Gamma \left(-{\tfrac {3}{2}}\right)&=&{\tfrac {4}{3}}{\sqrt {\pi }}&\approx &2.363\,271\,801\,207\\\Gamma \left(-{\tfrac {1}{2}}\right)&=&-2{\sqrt {\pi }}&\approx &-3.544\,907\,701\,811\\\Gamma \left({\tfrac {1}{2}}\right)&=&{\sqrt {\pi }}&\approx &1.772\,453\,850\,906\\\Gamma (1)&=&0!&=&1\\\Gamma \left({\tfrac {3}{2}}\right)&=&{\tfrac {1}{2}}{\sqrt {\pi }}&\approx &0.886\,226\,925\,453\\\Gamma (2)&=&1!&=&1\\\Gamma \left({\tfrac {5}{2}}\right)&=&{\tfrac {3}{4}}{\sqrt {\pi }}&\approx &1.329\,340\,388\,179\\\Gamma (3)&=&2!&=&2\\\Gamma \left({\tfrac {7}{2}}\right)&=&{\tfrac {15}{8}}{\sqrt {\pi }}&\approx &3.323\,350\,970\,448\\\Gamma (4)&=&3!&=&6\end{array}}$

連分數表示

伽馬函數也可以在複數域表示為兩個連分數之和：

$\Gamma (z)={\cfrac {e^{-1}}{2+0-z+1{\cfrac {z-1}{2+2-z+2{\cfrac {z-2}{2+4-z+3{\cfrac {z-3}{2+6-z+4{\cfrac {z-4}{2+8-z+5{\cfrac {z-5}{2+10-z+\ddots }}}}}}}}}}}}+{\cfrac {e^{-1}}{z+0-{\cfrac {z+0}{z+1+{\cfrac {1}{z+2-{\cfrac {z+1}{z+3+{\cfrac {2}{z+4-{\cfrac {z+2}{z+5+{\cfrac {3}{z+6-\ddots }}}}}}}}}}}}}}$

導數

Γ函數的微分

Γ函數（藍色）、Γ函數的微分（橘色），其中，大於50與小於-20的部分被截掉。

對任何複數z，滿足 Re(z) > 0，有

${\frac {{\rm {d}}^{n}}{{\rm {d}}z^{n}}}\,\Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}(\ln t)^{n}dt$

於是，對任何正整數 m

$\Gamma '(m+1)=m!\left(-\gamma +\sum _{k=1}^{m}{\frac {1}{k}}\right)\,$

其中γ是歐拉-馬歇羅尼常數。

複數值

$\Gamma (x+{\rm {i}}y)=\left\{\int _{1}^{\infty }{\frac {t^{x-1}}{\mathrm {e} ^{t}}}\cos(y\ln t){\rm {d}}t+\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}\left[{\frac {k+x}{(k+x)^{2}+y^{2}}}\right]\right\}+{\rm {i}}\left\{\int _{1}^{\infty }{\frac {t^{x-1}}{\mathrm {e} ^{t}}}\sin(y\ln t){\rm {d}}t-\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}{\left[{\frac {y}{(k+x)^{2}+y^{2}}}\right]}\right\}\,$

解析延拓

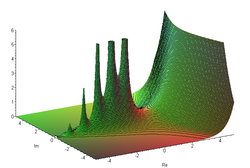
Γ函數的絕對值函數圖形

注意到在$\Gamma$函數的積分定義中若取$z\,$為實部大於零之複數、則積分存在，而且在右半複平面上定義一個全純函數。利用函數方程

$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin {\pi z}}}\quad (0<\mathrm {Re} (z)<1)$

並注意到函數$\sin(\pi z)\,$在整個複平面上有解析延拓，我們可以在$\mathrm {Re} (z)<1$時設

$\Gamma (z)={\dfrac {\pi }{\Gamma (1-z)\sin {\pi z}}}$

從而將$\Gamma \,$函數延拓為整個複平面上的亞純函數，它在$z=0,-1,-2,-3\cdots$有單極點，留數為

$\mathrm {Res} (\Gamma ,-n)={\dfrac {(-1)^{n}}{n!}}.$

程式實現

許多程式語言或試算表軟件有提供Γ函數或對數的Γ函數，例如EXCEL。而對數的Γ函數還要再取一次自然指數才能獲得Γ函數值。例如在EXCEL中，可使用GAMMALN函數，再用EXP[GAMMALN(X)]，即可求得任意實數的伽瑪函數的值。

• 例如在EXCEL中：EXP[GAMMALN(4/3)]=0.89297951156925

而在沒有提供Γ函數的程式環境中，也能夠過泰勒級數或斯特靈公式等方式來近似，例如Robert H. Windschitl在2002年提出的方法，其在十進制可獲得有效數字八位數的精確度，已足以填滿單精度浮點數的二進制有效數字24位元：

$\Gamma (z)\approx {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}{\sqrt {z\sinh {\frac {1}{z}}+{\frac {1}{810z^{6}}}}}\right)^{z}$

參見

• 雙伽瑪函數
• 多伽瑪函數
• 倒數伽瑪函數
• 伽瑪分佈

外部連結

• 神奇的Gamma函數(上)
• 神奇的Gamma函數(下)