積分

  「曲線下面積」重新導向至此。關於血漿中藥物濃度隨時間的定積分，請見「曲線下面積 (藥物代謝動力學)」。

  提示：此條目頁的主題不是得分。

積分（英語：integral）是微積分學與數學分析裡的一個核心概念。通常分為定積分和不定積分兩種。直觀地說，對於一個給定的正實值函數$f(x)$，$f(x)$在一個實數區間$[a,b]$上的定積分

$$\int _{a}^{b}f(x)\,\mathrm {d} x$$

可以在數值上理解為在$\textstyle Oxy$坐標平面上，由曲線$(x,f(x))$（$x\in [a,b]$），直線$x=a$，$x=b$以及$x$軸圍成的曲邊梯形的面積值。

函數 $f(x)$ 的定積分是函數與x軸圍成的曲邊梯形的有向面積：在x軸上方（藍色）的面積為正，下方（黃色）的面積為負。

$f(x)$的不定積分（或原函數）是指任何滿足導數是函數$f(x)$的函數$F(x)$。一個函數$f(x)$的不定積分不是唯一的：只要$F(x)$是$f(x)$的不定積分，那麼與之相差一個常數的函數 $F(x)+C$也是$f$的不定積分。

微積分基本定理是微積分學中的一條重要定理，由艾薩克·牛頓和戈特弗里德·威廉·萊布尼茨在十七世紀分別獨立發現。微積分基本定理將積分與微分建立聯繫，通過找出一個函數的原函數，即可方便地計算它在一個區間上的積分。積分和導數已成為高等數學中最基本的工具，並在自然科學和工程學中得到廣泛運用。

積分的一個嚴格的數學定義由波恩哈德·黎曼給出，因此習慣上我們常見的積分也稱為「黎曼積分」。黎曼的定義運用了極限的概念，把曲邊梯形設想為一系列矩形組合的極限。從十九世紀起，更高級的積分定義逐漸出現，有了對各種積分區間上的各種類型的函數的積分。對微分形式的積分是微分幾何中的基本概念。

對積分概念的推廣來自於物理學的需要，並體現在許多重要的物理定律中，尤其是電動力學。現代的積分概念基於測度論，主要是由昂利·勒貝格建立的勒貝格積分。

簡介

函數$f$在區間[0,1]上積分的近似 ■ 極大值（5部分）和■ 極小值（12部分）

積分發展的動力源自實際應用中的需求。實際操作中，有時候可以用粗略的方式進行估算一些未知量，但隨着科技的發展，很多時候需要知道精確的數值。要求簡單幾何形體的面積或體積，可以套用已知的公式。但如果游泳池是卵形、拋物型或更加不規則的形狀，就需要用積分來求出容積。物理學中，常常需要知道一個物理量（比如位移）對另一個物理量（比如力）的累積效果，這時也需要用到積分。

什麼是積分（動畫

我們以下面這個問題作為介紹積分概念的開始：

考慮平方根函數$f:\,x\mapsto {\sqrt {x}}$，其中$x\in [0,\,1]$。在區間[0,1]上，函數$f$「下方」的面積是多少？

問題中的「下方」面積，是指函數$y=f(x)$的圖象與x軸之間的部分的面積$S$（見右圖）。我們把這個面積稱為函數$f$在區間[0,1]上的積分，寫作：

$S=\int _{0}^{1}{\sqrt {x}}\,\mathrm {d} x\,\!.$

其中的$\mathrm {d} x$稱為積分變量，表示要求面積的範圍是用坐標軸橫軸的刻度計算；$\int _{0}^{1}$則表示從0開始算起，到1為止，稱為積分範圍或積分域，其中0稱為積分下界，1稱為積分上界，$\int$叫做積分號，是從拉長的字母S演變過來的。函數${\sqrt {x}}$寫在中間，稱為被積函數。

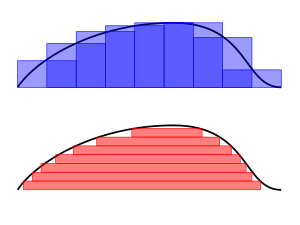
改進的方法是用更多的小方框來將函數圖象「覆蓋」，如右圖中的做法，就是將坐標軸橫軸[0,1]等分成5個部分：[0,0.2)、[0.2,0.4)、[0.4,0.6)、[0.6,0.8)、[0.8,1]，然後每一部分上放一個黃色的長方形（見右圖■）。這5個長方形的高度分別是函數在每個部分的極大值（也就是最右側的值）：${\sqrt {0.2}}$、${\sqrt {0.4}}$、${\sqrt {0.6}}$、${\sqrt {0.8}}$、$1$。這樣函數下方的部分就被5個黃色長方形覆蓋了，所以面積$S$小於5個黃色長方形面積之和：

${\sqrt {0.2}}\left(0.2-0\right)+{\sqrt {0.4}}\left(0.4-0.2\right)+{\sqrt {0.6}}\left(0.6-0.4\right)+{\sqrt {0.8}}\left(0.8-0.6\right)+{\sqrt {1}}\left(1-0.8\right)\approx 0.7497.\,\!$

求出了$S$的上限之後，用類似的方法可以求$S$的下限。同樣是將坐標軸等分成若干部分，然後在每個部分放上長方形，不過這時候長方形的高度需要是函數在這個部分的最小值，也就是最左側的值。比如，如果將橫軸等分成12個部分，然後按照以上的方法放上綠色長方形（如右圖■），那麼從圖中可以看出，$S$必定大於綠色長方形面積之和：

${\sqrt {\frac {0}{12}}}\left({\frac {1}{12}}-0\right)+{\sqrt {\frac {1}{12}}}\left({\frac {2}{12}}-{\frac {1}{12}}\right)+\cdots +{\sqrt {\frac {11}{12}}}\left(1-{\frac {11}{12}}\right)\approx 0.6203.\,\!$

於是，面積$S$的取值介於0.6203和0.7497之間。要取得更加精確的估計，可以將橫軸細分成更多的部分，並按照同樣的方法放置長方形，計算長方形的面積之和。隨着長方形越來越多，每個長方形越來越「細」，計算出的$S$的範圍會越來越窄，最後得出$S$的精確值。

以上的方法可能出現的「漏洞」，是所謂的「取值範圍」不一定會越來越小，最後聚集到同一個值上。雖然直觀上來說，由於函數下方的圖形面積是確定的，只要不斷地用相似的形狀「逼近」，最後總會趨向函數下方圖形的真實面積。然而，對於某些「病態」的函數，以上的方法是無法得到確定的數值的。十九世紀的數學家波恩哈德·黎曼證明了，對於滿足某些條件的良態函數，以上的方法一定能求出函數下方的面積。現代的數學家將這種方法求出的面積稱為黎曼積分，並給出了嚴格的定義（見#嚴格定義一節）。對於那些無法用黎曼的方法定義「函數下方圖形面積」的函數，黎曼之後的數學家發展出了一些更寬泛的定義，讓這些函數也能定義積分。

術語和標記

如果一個函數的積分存在，並且有限，就說這個函數是可積的。一般來說，被積函數不一定只有一個變量，積分域也可以是不同維度的空間，甚至是沒有直觀幾何意義的抽象空間。如同上面介紹的，對於只有一個變量 $x$的實值函數 $f$ ， $f$在閉區間 $[a,b]$上的積分記作

$\int _{a}^{b}f(x)\,\mathrm {d} x.$

其中的$\mathrm {d} x$除了表示$x$是$f$ 中要進行積分的那個變量（積分變量）之外，還可以表示不同的含義。在黎曼積分中，$\mathrm {d} x$表示分割區間的標記；在勒貝格積分中，表示一個測度；或僅僅表示一個獨立的量（微分形式）。一般的區間或者積分範圍$J$，$J$上的積分可以記作$\int _{J}f(x)\,\mathrm {d} x.$

如果變量不只一個，比如說在二重積分中，函數$f(x,y)\,\!$ 在區域D上的積分記作

$\iint _{D}f(x,y)\,\!\,\mathrm {d} \sigma$ 或者 $\iint _{D}f(x,y)\,\!\,\mathrm {d} x\mathrm {d} y$

其中 $\mathrm {d} \sigma$ 與區域D對應，是相應積分域中的微分元。

嚴格定義

定義積分的方法不止一種，各種定義之間也不是完全等價的。其中的差別主要是在定義某些特殊的函數：在某些積分的定義下這些函數不可積分，但在另一些定義之下它們的積分存在。然而有時也會因為教學的原因造成定義上的差別。最常見的積分定義是黎曼積分和勒貝格積分。

黎曼積分

主條目：黎曼積分

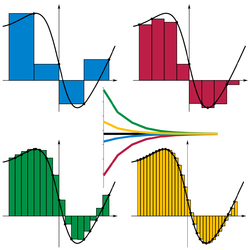
在閉區間上取定一個（不規則的）取樣分割後獲得的黎曼和

黎曼積分得名於德國數學家波恩哈德·黎曼，建立在函數在區間取樣分割後的黎曼和之上。設有閉區間$[a,b]$，那麼$[a,b]$的一個分割是指在此區間中取一個有限的點列$a=x_{0}<x_{1}<x_{2}<\ldots <x_{n}=b$。每個閉區間$[x_{i},x_{i+1}]$叫做一個子區間。定義$\lambda$ 為這些子區間長度的最大值：$\lambda =\max(x_{i+1}-x_{i})$，其中$0\leq i\leq n-1$。而閉區間$[a,b]$上的一個取樣分割是指在進行分割$a=x_{0}<x_{1}<x_{2}<\ldots <x_{n}=b$後，於每一個子區間中$[x_{i},x_{i+1}]$取出一點 $x_{i}\leq t_{i}\leq x_{i+1}$。

確定的子區間上不同的取樣方式構成的黎曼和：■ 右端值，■ 極小值， ■ 極大值， ■ 左端值。

對一個在閉區間$[a,b]$有定義的實值函數$f$，$f$關於取樣分割$x_{0},\ldots ,x_{n}$ 、$t_{0},\ldots ,t_{n-1}$的黎曼和定義為以下和式：

$\sum _{i=0}^{n-1}f(t_{i})(x_{i+1}-x_{i})$

和式中的每一項是子區間長度$x_{i+1}-x_{i}$與在$t_{i}$處的函數值$f(t_{i})$的乘積。直觀地說，就是以標記點$t_{i}$到X軸的距離為高，以分割的子區間為長的矩形的面積。

最簡單的取樣分割方法是將區間均勻地分成若干個長度相等的子區間，然後在每個子區間上按相同的準則取得標記點。例如取每個子區間右端$t_{i}=x_{i+1}$（見左圖左上角）或者取每個子區間上函數的極大值對應的$t_{i}$（左圖左下角）等等。不同的取樣分割方式得到的黎曼和一般都不相同，而如果當$\lambda$足夠小的時候，所有的黎曼和都趨於某個極限，那麼這個極限就叫做函數$f$在閉區間$[a,b]$上的黎曼積分。即，$S$是函數$f$在閉區間$[a,b]$上的黎曼積分，當且僅當對於任意的$\epsilon >0$，都存在$\delta >0$，使得對於任意的取樣分割$x_{0},\ldots ,x_{n}$、$t_{0},\ldots ,t_{n-1}$，只要它的子區間長度最大值$\lambda \leq \delta$ ，就有：

$\left|\sum _{i=0}^{n-1}f(t_{i})(x_{i+1}-x_{i})-S\right|<\epsilon .\,$

也就是說，對於一個函數$f$，如果在閉區間$[a,b]$上，無論怎樣進行取樣分割，只要它的子區間長度最大值足夠小，函數$f$的黎曼和都會趨向於一個確定的值$S$，那麼$f$在閉區間$[a,b]$上的黎曼積分存在，並且定義為黎曼和的極限$S$。這時候稱函數$f$為黎曼可積的。將$f$在閉區間$[a,b]$上的黎曼積分記作：

$\int _{a}^{b}f(x)\mathrm {d} x.$

勒貝格積分

主條目：勒貝格積分

勒貝格積分的出現源於概率論等理論中對更為不規則的函數的處理需要。黎曼積分無法處理這些函數的積分問題。因此，需要更為廣義化的積分概念，使得更多的函數能夠定義積分。同時，對於黎曼可積的函數，新積分的定義不應當與之衝突。勒貝格積分就是這樣的一種積分。 黎曼積分對初等函數和分段連續的函數定義了積分的概念，勒貝格積分則將積分的定義推廣到測度空間裡。

勒貝格積分的概念定義在測度的概念上。測度是日常概念中測量長度、面積的推廣，將其以公理化的方式定義。黎曼積分實際可以看成是用一系列矩形來儘可能鋪滿函數曲線下方的圖形，而每個矩形的面積是長乘寬，或者說是兩個區間之長度的乘積。測度為更一般的空間中的集合定義了類似長度的概念，從而能夠「測量」更不規則的函數曲線下方圖形的面積，從而定義積分。在一維實空間中，一個區間 A = [a, b] 的勒貝格測度μ(A)是區間的右端值減去左端值， b − a。這使得勒貝格積分和正常意義上的黎曼積分相兼容。在更複雜的情況下，積分的集合可以更加複雜，不再是區間，甚至不再是區間的交集或併集，其「長度」則由測度來給出。

給定一個集合$\Omega$上的$\sigma -$代數${\mathcal {F}}$以及${\mathcal {F}}$上的一個測度$\mu$，那麼對於${\mathcal {F}}$中的一個元素$A\subset \Omega$，定義指示函數$1_{A}$關於測度$\mu$的積分為：

黎曼積分（藍色）和勒貝格積分（紅色）

$\int 1_{A}\,\mathrm {d} \mu =\mu (A)$

再定義可測的非負簡單函數$f=\sum _{i=1}^{n}a_{i}1_{A_{i}}$（其中 $A_{i}\in {\mathcal {F}},\,\,a_{i}\geqslant 0$）的積分為：

$\int f\,\mathrm {d} \mu =\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)\,\mathrm {d} \mu =\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,\mathrm {d} \mu =\sum _{i=1}^{n}a_{i}\mu (A_{i})$

對於一般的函數$f:\Omega \rightarrow \mathbb {R}$，如果對每個區間$(a,b]$，都滿足 $f^{-1}\left((a,b]\right)\in {\mathcal {F}}$，那麼測度論中定義$f$是可測函數。對於一個非負的可測函數$f$，它的積分定義為：

$\int f\,\mathrm {d} \mu =\sup {\bigg \{}g,\quad g$為簡單函數，並且$f-g$恆大於零$.\,{\bigg \}}$

這個積分可以用以下的方式逼近：

$\int f\,\mathrm {d} \mu =\lim _{n\to +\infty }\left[\sum _{k=0}^{n2^{n}-1}{\frac {k}{2^{n}}}\mu \left({\frac {k}{2^{n}}}\leqslant f<{\frac {k+1}{2^{n}}}\right)+n\mu (f\geqslant n)\right]=\lim _{n\to +\infty }\left[{\frac {1}{2^{n}}}\sum _{k=0}^{n2^{n}-1}\mu \left({\frac {k}{2^{n}}}\leqslant f\right)\right]$

直觀上，這種逼近方式是將$f$的值域分割成等寬的區段，再考察每段的「長度」，用其測度表示，再乘以區段所在的高度。其覆蓋之處如右圖中的紅色區域所示。佛蘭德（Folland）總結說，「黎曼積分是把定義域區間[a, b]劃分為子區間」，而勒貝格積分則是「劃分$f$的值域」。

至於一般的（有正有負的）可測函數$f$，它的積分是函數曲線在x軸上方「圍出」的面積，減去曲線在x軸下方「圍出」的面積。嚴格定義需要引進「正部函數」和「負部函數」的概念：

$f^{+}:$ 如果$f(x)\geqslant 0,$ 則$f^{+}(x)=f(x),$ 否則$f^{+}(x)=0.$

$f^{-}:$ 如果$f(x)\leqslant 0,$ 則$f^{-}(x)=-f(x),$ 否則$f^{-}(x)=0.$

可以驗證，總有$f(x)=f^{+}(x)-f^{-}(x).$ 而$f$的積分定義為：$\int f\,\mathrm {d} \mu =\int f^{+}\,\mathrm {d} \mu -\int f^{-}\,\mathrm {d} \mu$

以上定義有意義僅當$\int f^{+}\,\mathrm {d} \mu$和$\int f^{-}\,\mathrm {d} \mu$中至少有一個的值是有限的（否則會出現無窮大減無窮大的情況），這時稱$f$的勒貝格積分存在或積分有意義。如果$\int f^{+}\,\mathrm {d} \mu$和$\int f^{-}\,\mathrm {d} \mu$都是有限的，那麼稱$f$可積。

給定一個可測集合$A$，可以定義可積函數在$A$上的積分為：

$\int _{A}f\,\mathrm {d} \mu =\int f1_{A}\,\mathrm {d} \mu .$

其他定義

除了黎曼積分和勒貝格積分以外，還有若干不同的積分定義，適用於不同種類的函數。

• 達布積分：等價於黎曼積分的一種定義，比黎曼積分更加簡單，可用來幫助定義黎曼積分。
• 黎曼－斯蒂爾傑斯積分：黎曼積分的推廣，用一般的函數g(x)代替x作為積分變量，也就是將黎曼和中的$(x_{i+1}-x_{i})$推廣為$(g(x_{i+1})-g(x_{i}))$。
• 勒貝格－斯蒂爾傑斯積分：勒貝格積分的推廣，推廣方式類似於黎曼－斯蒂爾傑斯積分，用有界變差函數g代替測度$\mu$。
• 哈爾積分：由阿爾弗雷德·哈爾於1933年引入，用來處理局部緊拓撲群上的可測函數的積分，參見哈爾測度。
• 伊藤積分：由伊藤清於二十世紀五十年代引入，用於計算包含隨機過程如維納過程或半鞅的函數的積分。

性質

通常意義上的積分都滿足一些基本的性質。以下的${\mathcal {I}}$在黎曼積分意義上表示一個區間，在勒貝格積分意義下表示一個可測集合。

線性

積分是線性的。如果一個函數$f$可積，那麼它乘以一個常數後仍然可積。如果函數$f$和$g$可積，那麼它們的和與差也可積。

$\int _{\mathcal {I}}(\alpha f+\beta g)=\alpha \int _{\mathcal {I}}f+\beta \int _{\mathcal {I}}g\,$

所有在${\mathcal {I}}$上可積的函數構成了一個線性空間。黎曼積分的意義上，所有區間[a, b]上黎曼可積的函數$f$和$g$都滿足：

$\int _{a}^{b}(\alpha f+\beta g)(x)\,\mathrm {d} x=\alpha \int _{a}^{b}f(x)\,\mathrm {d} x+\beta \int _{a}^{b}g(x)\,\mathrm {d} x.\,$

所有在可測集合${\mathcal {I}}$上勒貝格可積的函數$f$和$g$都滿足：

$\int _{\mathcal {I}}(\alpha f+\beta g)\,\mathrm {d} \mu =\alpha \int _{\mathcal {I}}f\,\mathrm {d} \mu +\beta \int _{\mathcal {I}}g\,\mathrm {d} \mu .$

在積分區域上，積分有可加性。黎曼積分意義上，如果一個函數$f$在某區間上黎曼可積，那麼對於區間內的三個實數a, b, c，有

$\int _{a}^{c}f(x)\,\mathrm {d} x=\int _{a}^{b}f(x)\,\mathrm {d} x+\int _{b}^{c}f(x)\,\mathrm {d} x\,$

如果函數$f$在兩個不相交的可測集${\mathcal {I}}$和${\mathcal {J}}$上勒貝格可積，那麼

$\int _{{\mathcal {I}}\cup {\mathcal {J}}}f\,\mathrm {d} \mu =\int _{\mathcal {I}}f\,\mathrm {d} \mu +\int _{\mathcal {J}}f\,\mathrm {d} \mu .$

如果函數$f$勒貝格可積，那麼對任意$\epsilon >0$，都存在$\delta$，使得${\mathcal {F}}$中任意的元素$A$，只要$\mu (A)<\delta$，就有$\int _{A}\left|f\right|\,\mathrm {d} \mu <\epsilon$

保號性

如果一個函數$f$在某個區間上黎曼可積，並且在此區間上大於等於零。那麼它在這個區間上的積分也大於等於零。如果$f$勒貝格可積並且幾乎總是大於等於零，那麼它的勒貝格積分也大於等於零。作為推論，如果兩個${\mathcal {I}}$上的可積函數$f$和$g$相比， $f$（幾乎）總是小於等於$g$，那麼$f$的（勒貝格）積分也小於等於$g$的（勒貝格）積分。

如果黎曼可積的非負函數$f$在${\mathcal {I}}$上的積分等於0，那麼除了有限個點以外，$f=0$。如果勒貝格可積的非負函數$f$在${\mathcal {I}}$上的積分等於0，那麼$f$幾乎處處為0。如果${\mathcal {F}}$中元素$A$的測度$\mu (A)$等於0，那麼任何可積函數在$A$上的積分等於0。

函數的積分表示了函數在某個區域上的整體性質，改變函數某點的取值不會改變它的積分值。對於黎曼可積的函數，改變有限個點的取值，其積分不變。對于勒貝格可積的函數，某個測度為0的集合上的函數值改變，不會影響它的積分值。如果兩個函數幾乎處處相同，那麼它們的積分相同。如果對${\mathcal {F}}$中任意元素$A$，可積函數$f$在$A$上的積分總等於（大於等於）可積函數$g$在$A$上的積分，那麼$f$幾乎處處等於（大於等於）$g$。

介值性質

如果$f$在${\mathcal {I}}$上可積， $M$和$m$分別是$f$在${\mathcal {I}}$上的最大值和最小值，那麼：

$mL({\mathcal {I}})\leqslant \int _{\mathcal {I}}f\leqslant ML({\mathcal {I}})$

其中的$L({\mathcal {I}})$在黎曼積分中表示區間${\mathcal {I}}$的長度，在勒貝格積分中表示${\mathcal {I}}$的測度。

絕對連續性

積分的絕對連續性表明，如果函數在某區間或集合上可積，那麼當積分區域是近乎全區域的時候，積分的值也會逼近在全區域上的積分值。如果函數$f$在某區間${\mathcal {I}}$上黎曼可積，那麼對於滿足${\mathcal {I}}_{n}\subset {\mathcal {I}}_{n+1}$，$\lim _{n\to \infty }{\mathcal {I}}_{n}={\mathcal {I}}$的區間序列$\left({\mathcal {I}}_{n}\right)_{n\in \mathbb {N} }$，有

$\lim _{n\to \infty }\int _{{\mathcal {I}}_{n}}f(x)\,\mathrm {d} x=\int _{\mathcal {I}}f(x)\,\mathrm {d} x$

積分不等式

涉及積分的基本不等式可以看作是一些離散不等式的類比。如柯西不等式的積分版本：假如有函數$f$和$g$使得$fg$、$f^{2}$、$g^{2}$都在區間${\mathcal {I}}$上黎曼可積，那麼

$\left(\int _{\mathcal {I}}(fg)(x)\,\mathrm {d} x\right)^{2}\leq \left(\int _{\mathcal {I}}f(x)^{2}\,\mathrm {d} x\right)\left(\int _{\mathcal {I}}g(x)^{2}\,\mathrm {d} x\right).$

而更廣泛的赫爾德不等式也有積分版本。設有正實數$p$和$q$，其倒數和為1：${\frac {1}{p}}+{\frac {1}{q}}=1$，則對黎曼可積函數$f$和$g$，有以下不等關係（在下式各項有意義的時候）：

$\left|\int f(x)g(x)\,\mathrm {d} x\right|\leqslant \left(\int \left|f(x)\right|^{p}\,\mathrm {d} x\right)^{\frac {1}{p}}\left(\int \left|g(x)\right|^{q}\,\mathrm {d} x\right)^{\frac {1}{q}}.$

可以看出柯西不等式是赫爾德不等式在$p=q=2$的時候的特例。

此外閔可夫斯基不等式也有積分版本。設有正實數$p\geqslant 1$，則對黎曼可積函數$f$和$g$，有以下不等關係：

$\left(\int \left|f(x)+g(x)\right|^{p}\,\mathrm {d} x\right)^{\frac {1}{p}}\leq \left(\int \left|f(x)\right|^{p}\,\mathrm {d} x\right)^{\frac {1}{p}}+\left(\int \left|g(x)\right|^{p}\,\mathrm {d} x\right)^{\frac {1}{p}}.$

對于勒貝格可積的函數，類似的不等式可以幫助構建$L^{p}$空間。

一個函數$f$可積當且僅當函數$|f|$可積，並且$f$的積分的絕對值，小於等於其絕對值的積分：$\left|\int _{\mathcal {I}}f\right|\leqslant \int _{\mathcal {I}}|f|$。如果函數$f$勒貝格可積，那麼$|f|$幾乎處處有限。

微積分基本定理

主條目：微積分基本定理

微積分基本定理是將微分運算（求導運算）和積分運算（原函數）聯繫在一起的基本定理。從基本定理可以看出微分和積分運算之間的互逆關係。定理敘述如下：

設有在閉區間[a, b]上連續的可積函數$f$。考慮積分上限函數$F(x)=\int _{a}^{x}f(t)\,\mathrm {d} t$，則$F$在閉區間[a, b]上連續，在開區間(a, b) 上可導，並且對開區間(a, b) 中任意的$x$有：

$F'(x)=f(x)$

微積分基本定理的一個實用的直接推論，也被稱為微積分第二基本定理：

設有在閉區間[a, b]上連續的可積函數$f$。考慮它的一個原函數$F(x)$，即：

$F'(x)=f(x)$

則$f$在區間[a, b]上的定積分滿足：

$\int _{a}^{b}f(t)\mathrm {d} t=F(b)-F(a).$

推廣

反常積分

主條目：反常積分

$\int _{0}^{\infty }{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}=\pi$
這是一個既含有無限積分區間，被積函數也無限的積分

狹義的黎曼積分中，被積函數是定義在閉區間（長度有限）上的函數，因此取值也是在有限區間中。反常積分也稱為廣義積分，是對更一般區間上的函數定義的積分，研究在狹義黎曼積分的被積函數條件沒有滿足時，是否能夠有積分的定義。一個基本的情形是，被積函數在半開區間[a, b)上有定義，然而在自變量趨向開區間的某一端（比如說b）時，函數有「瑕點」（函數值趨向無窮或沒有極限）。這時候，考察被積函數在閉區間[a, b - ε]上的積分值$I_{\epsilon }$，如果當其中的正實數 ε 趨向於0的時候，積分值$I_{\epsilon }$趨於一個極限$I$，那麼就稱被積函數在[a, b)上廣義可積，並且稱其為瑕積分$I$。這個定義也可以簡單地記作：

$\int _{a}^{b}f(x)\,\mathrm {d} x=\lim _{\epsilon \to 0}\int _{a}^{b-\epsilon }f(x)\,\mathrm {d} x$

另一個基本的情形是區間長度為無限大的情形，稱為無窮限廣義積分。比如說被積函數在在閉區間[a, ∞)上有定義。考慮被積函數在閉區間[a, b]上的積分值$I_{b}$，如果當b趨向正無窮大的時候，積分值$I_{b}$趨於一個極限$I$，那麼就稱被積函數在[a, ∞)上廣義可積，並且稱為無窮限積分$I$。這個定義也可以簡單地記作：

$\int _{a}^{\infty }f(x)\,\mathrm {d} x=\lim _{b\to \infty }\int _{a}^{b}f(x)\,\mathrm {d} x$

其餘更加複雜的情形包括瑕點在區間內部，或者同時包含了無窮限的情形等等。這些情形都可以拆分為基本情形的組合，然後使用以上的方法探討廣義積分的存在性。比如，考慮函數$f(x)={\frac {1}{(x+1){\sqrt {x}}}}$在正實數區間（0到正無窮）上的積分（如右圖所示）。這是一個雙重廣義積分。一方面函數在0處有瑕點（在0附近趨向正無窮），另一方面函數積分區域是無窮限（直到正無窮大）。這時候可以將這個積分分割為兩個部分來考察。比如說以1為界限，左右分割為0到1的積分和1到正無窮大的積分。

首先考察1到正無窮大的部分，依據上述方法，可以首先考察$f(x)$在閉區間[1, t]上的積分：

$I_{t}=\int _{1}^{t}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}=2\arctan {\sqrt {t}}-{\frac {\pi }{2}}$

當實數t趨於無窮大的時候，上述積分值的極限為$\lim _{t\to \infty }\left(2\arctan {\sqrt {t}}-{\frac {\pi }{2}}\right)={\frac {\pi }{2}}.$ 所以$f(x)$從1到正無窮大的積分可以定義為：

$\int _{1}^{\infty }{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}=\lim _{t\to \infty }\int _{1}^{t}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}={\frac {\pi }{2}}$

同樣地，考察從0到1的部分，可以首先考察$f(x)$在閉區間[s, 1]上的積分：

$I_{s}=\int _{s}^{1}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}={\frac {\pi }{2}}-2\arctan {\sqrt {s}}$

當正實數s趨於0的時候，上述積分值的極限為$\lim _{s\to 0}\left({\frac {\pi }{2}}-2\arctan {\sqrt {s}}\right)={\frac {\pi }{2}}.$ 所以$f(x)$從0到1的積分可以定義為：

$\int _{0}^{1}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}=\lim _{s\to 0}\int _{s}^{1}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}={\frac {\pi }{2}}$

因此可以定義$f(x)={\frac {1}{(x+1){\sqrt {x}}}}$在正實數區間（0到正無窮）上的積分為這兩部分的和：

$\int _{0}^{\infty }{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}=\int _{0}^{1}{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}+\int _{1}^{\infty }{\frac {\mathrm {d} x}{(x+1){\sqrt {x}}}}={\frac {\pi }{2}}+{\frac {\pi }{2}}=\pi$

多重積分

主條目：多重積分

狹義積分的積分範圍是實數的一個區間或者可測子集。多重積分將積分範圍擴展到多維空間中的區域或可測子集。比如說二重積分的積分範圍是平面上的一個區域。這時候積分$\int _{D}f(x)\,\mathrm {d} x$中的變量$x$可以是（賦予了拓撲結構的）向量空間裡面的一個向量。富比尼定理證明，在一定條件下，多重積分可以轉換為累次積分。也就是說，在多維空間上的積分可以通過轉化為多個嵌套的一重積分來計算。通常的方法是將多重的積分變量轉變為各個坐標指標上的積分變量。例如，考慮以下二重積分：

$\int _{C}e^{-x^{2}-y^{2}}\,\mathrm {d} \sigma .$

其中的$C=\{(x,y)\;|\;x^{2}+y^{2}\leqslant 1\}$是一個半徑為1的圓盤。這個二重積分可以轉變成：

$\int _{C}e^{-x^{2}-y^{2}}\,\mathrm {d} \sigma =\int _{-1}^{1}\int _{-{\sqrt {1-y^{2}}}}^{\sqrt {1-y^{2}}}e^{-x^{2}-y^{2}}\,\mathrm {d} x\mathrm {d} y=\int _{0}^{2\pi }\int _{0}^{1}e^{-r^{2}}\,r\mathrm {d} r\mathrm {d} \theta .$

路徑積分與曲面積分

主條目：路徑積分和曲面積分

路徑積分也稱曲線積分，可以看作是區間上積分的推廣。積分的範圍不是區間（直線段），而是高維空間中的有向曲線。後者稱為積分路徑。路徑積分有很多種類，當積分路徑為閉合曲線時，稱為環路積分或圍道積分。路徑積分的被積函數可以是標量函數（標量場）或向量函數（向量場）。如果被積函數F是一個梯度場，那麼F的曲線積分與所取的路徑無關，而只與路徑的起點和終點的選取有關。與路徑積分類似，平面區域的二重積分可以推廣為在高維空間中的（有向）曲面上進行積分，稱為曲面積分。路徑積分和曲面積分是物理學中很重要的工具，例如計算電場或重力場中的做功、量子力學中計算粒子出現的概率，會用到路徑積分。流體力學中計算流體的流量、電力學中使用高斯定律計算電場和電荷分布時，會用到曲面積分。

種類

• 黎曼積分
• 達布積分
• 勒貝格積分
• 黎曼-斯蒂爾吉斯積分
• 數值積分

參見

• 微積分基本定理
• 不定積分
• 定積分
• 積分符號
• 積分表
• 曲線下面積 (藥物代謝動力學)