提示 :此条目页的主题不是
倒数 。
一个实值函数的图像曲线。函数在一点的导数等于它的图像上这一点处之切线 的斜率 。 导数 (英语:derivative )是微积分 学中的一个概念。函数 在某一点的导数是指这个函数在这一点附近的变化率(即函数在这一点的切线斜率)。导数的本质是通过极限 的概念对函数进行局部的线性逼近。当函数
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
h
{\displaystyle h}
h
{\displaystyle h}
h
{\displaystyle h}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
d
f
d
x
(
x
0
)
{\displaystyle {\frac {\mathrm {d} f}{\mathrm {d} x}}(x_{0})}
d
f
d
x
|
x
=
x
0
{\displaystyle \left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=x_{0}}}
运动学 中,物体的位移 对于时间 的导数就是物体的瞬时速度 [ 1] :155 。
导数是函数的局部性质。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导(可微分),否则称为不可导(不可微分)。如果函数的自变量和取值都是实数的话,那么函数在某一点的导数就是该函数所代表的曲线在这一点上的切线 斜率 。
对于可导的函数
f
{\displaystyle f}
x
↦
f
′
(
x
)
{\displaystyle x\mapsto f'(x)}
f
{\displaystyle f}
导函数 。寻找已知的函数在某点的导数或其导函数的过程称为求导 (英语:differentiation )。反之,已知导函数也可以倒过来求原来的函数,即不定积分 。微积分基本定理 说明了求原函数与积分 是等价的[ 1] :372 。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
一个动画,给出了一个直观的导数概念,因为参数变化时函数的“摆动”会改变。
直观上
f
(
x
)
−
f
(
a
)
{\displaystyle f(x)-f(a)}
a
{\displaystyle a}
x
{\displaystyle x}
f
(
x
)
−
f
(
a
)
x
−
a
{\displaystyle {\frac {f(x)-f(a)}{x-a}}}
代表的是从
a
{\displaystyle a}
x
{\displaystyle x}
x
{\displaystyle x}
a
{\displaystyle a}
a
{\displaystyle a}
以此为动机,若实函数
f
{\displaystyle f}
实数
a
{\displaystyle a}
a
{\displaystyle a}
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
{\displaystyle \lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}}
存在则称
f
{\displaystyle f}
a
{\displaystyle a}
可导 ,并称这个极限为
f
{\displaystyle f}
a
{\displaystyle a}
导数[ 2] :117-118 ,记为
f
′
(
a
)
{\displaystyle f^{\prime }(a)}
d
f
d
x
|
x
=
a
{\displaystyle \left.{\frac {\mathrm {d} f}{\mathrm {d} x}}\right|_{x=a}}
d
f
d
x
(
a
)
{\displaystyle {\frac {\mathrm {d} f}{\mathrm {d} x}}(a)}
[ 1] :154 。
根据函数极限的定义 ,导数定义部分的 "存在
δ
>
0
{\displaystyle \delta >0}
x
∈
D
f
{\displaystyle x\in D_{f}}
0
<
|
x
−
a
|
<
δ
{\displaystyle 0<|x-a|<\delta }
h
=
x
−
a
{\displaystyle h=x-a}
0
{\displaystyle 0}
δ
>
0
{\displaystyle \delta >0}
h
{\displaystyle h}
a
+
h
∈
D
f
{\displaystyle a+h\in D_{f}}
0
<
|
h
|
<
δ
{\displaystyle 0<|h|<\delta }
lim
h
→
0
f
(
a
+
h
)
−
f
(
a
)
h
{\displaystyle \lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}}
定义为导数原始极限表达式的简记 ,而非另一种自动合法的导数定义。但如果存在
r
>
0
{\displaystyle r>0}
f
{\displaystyle f}
(
a
−
r
,
a
+
r
)
{\displaystyle (a-r,\,a+r)}
F
{\displaystyle F}
{
h
∈
R
|
(
h
≠
0
)
∧
(
|
h
|
<
r
)
}
{\displaystyle \{h\in \mathbb {R} \,|\,(h\neq 0)\wedge (|h|<r)\}}
为定义域,然后以
F
(
h
)
=
f
(
a
+
h
)
−
f
(
a
)
h
{\displaystyle F(h)={\frac {f(a+h)-f(a)}{h}}}
为对应规则的函数,那以下的极限式
lim
h
→
0
F
(
h
)
=
f
′
(
a
)
{\displaystyle \lim _{h\to 0}F(h)=f^{\prime }(a)}
就可以把以
h
{\displaystyle h}
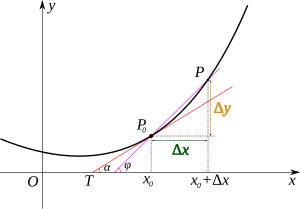
当函数定义域和取值都在实数 域中的时候,导数可以表示函数的曲线上的切线斜率。如右图所示,设
P
0
{\displaystyle P_{0}}
P
{\displaystyle P}
P
{\displaystyle P}
P
0
{\displaystyle P_{0}}
P
P
0
{\displaystyle PP_{0}}
P
0
T
{\displaystyle P_{0}T}
P
0
T
{\displaystyle P_{0}T}
P
0
{\displaystyle P_{0}}
若曲线为一函数
y
=
f
(
x
)
{\displaystyle y=f(x)}
P
P
0
{\displaystyle PP_{0}}
tan
φ
=
Δ
y
Δ
x
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
{\displaystyle \tan \varphi ={\frac {\Delta y}{\Delta x}}={\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}}
当
P
0
{\displaystyle P_{0}}
P
0
T
{\displaystyle P_{0}T}
P
P
0
{\displaystyle PP_{0}}
Δ
x
→
0
{\displaystyle \Delta x\to 0}
φ
→
α
{\displaystyle \varphi \to \alpha }
P
0
T
{\displaystyle P_{0}T}
tan
α
{\displaystyle \tan \alpha }
tan
α
=
lim
Δ
x
→
0
tan
φ
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
{\displaystyle \tan \alpha =\lim _{\Delta x\to 0}\tan \varphi =\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}}
上式与一般定义中的导数定义完全相同,也就是说
f
′
(
x
0
)
=
tan
α
{\displaystyle f'(x_{0})=\tan \alpha }
y
=
f
(
x
)
{\displaystyle y=f(x)}
P
0
(
x
0
,
f
(
x
0
)
)
{\displaystyle P_{0}(x_{0},f(x_{0}))}
[ 2] :117 [ 1] :153
若函数
f
(
x
)
{\displaystyle \;f(x)\;}
区间
I
{\displaystyle \;I\;}
f
(
x
)
{\displaystyle \;f(x)\;}
区间
I
{\displaystyle \;I\;}
I
{\displaystyle \;I\;}
x
{\displaystyle \;x\;}
f
{\displaystyle \;f\;}
x
↦
f
′
(
x
)
{\displaystyle x\mapsto f'(x)}
f
(
x
)
{\displaystyle \;f(x)\;}
导函数 [ 1] :155 ,记作:
y
′
{\displaystyle \;y'\;}
f
′
(
x
)
{\displaystyle f'(x)\;}
d
f
d
x
(
x
)
{\displaystyle {\tfrac {\mathrm {d} f}{\mathrm {d} x}}(x)}
f
(
x
)
{\displaystyle f(x)\;}
x
0
{\displaystyle x_{0}\;}
函数值 。但在不至于混淆的情况下,通常也可以说导函数为导数。
由于对每一个可导的函数
f
(
x
)
{\displaystyle \;f(x)\;}
f
′
(
x
)
{\displaystyle f'(x)\;}
算子 。这个算子称为微分算子,一般记作
D
{\displaystyle D}
d
d
x
{\displaystyle {\tfrac {\mathrm {d} }{\mathrm {d} x}}}
[ 3]
D
(
x
↦
1
)
=
(
x
↦
0
)
D
(
x
↦
x
)
=
(
x
↦
1
)
D
(
x
↦
x
2
)
=
(
x
↦
2
⋅
x
)
{\displaystyle {\begin{aligned}D(x\mapsto 1)&=(x\mapsto 0)\\D(x\mapsto x)&=(x\mapsto 1)\\D(x\mapsto x^{2})&=(x\mapsto 2\cdot x)\end{aligned}}}
由于微分算子的输出值仍然是函数,可以继续求出它在某一点的取值。比如说对于函数
f
(
x
)
=
x
2
{\displaystyle \;f(x)=x^{2}\;}
D
(
f
)
=
(
x
↦
2
⋅
x
)
{\displaystyle D(f)=(x\mapsto 2\cdot x)}
所以
D
(
f
)
(
x
)
=
2
x
{\displaystyle D(f)(x)=2x}
D
(
f
)
(
1.4
)
=
2
×
1.4
=
2.8
{\displaystyle D(f)(1.4)=2\times 1.4=2.8}
微分 也是一种线性描述函数在一点附近变化的方式。微分和导数是两个不同的概念。但是,对一元函数来说,可微与可导是完全等价的。可微的函数,其微分等于导数乘以自变量的微分
d
x
{\displaystyle \mathrm {d} x}
微商 。函数
y
=
f
(
x
)
{\displaystyle y=f(x)}
d
y
=
f
′
(
x
)
d
x
{\displaystyle \mathrm {d} y=f'(x)\mathrm {d} x}
[ 4]
导数和积分 的发现是微积分 发明的关键一步。17世纪以来,光学透镜 的设计以及炮弹弹道 轨迹的计算促使欧洲的数学家对曲线的切线进行研究。1630年代,法国数学家吉尔·德·罗伯瓦尔 作出了最初的尝试[ 5] 费马 在计算切线时已经使用了无穷小量 的概念[ 注 1] [ 6] :52 。
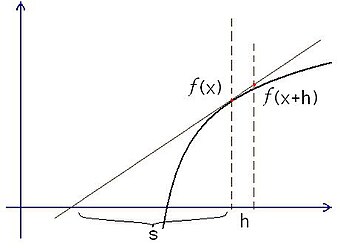
如右图,费马考虑曲线
f
(
x
)
{\displaystyle f(x)}
x
{\displaystyle x}
s
s
+
h
=
f
(
x
)
f
(
x
+
h
)
{\displaystyle {\frac {s}{s+h}}={\frac {f(x)}{f(x+h)}}}
对上式变形后得到:
s
=
f
(
x
)
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle s={\frac {f(x)}{\frac {f(x+h)-f(x)}{h}}}}
对于具体的函数
f
(
x
)
{\displaystyle f(x)}
f
(
x
)
=
x
3
{\displaystyle f(x)=x^{3}}
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle {\frac {f(x+h)-f(x)}{h}}}
h
{\displaystyle h}
s
{\displaystyle s}
f
(
x
)
{\displaystyle f(x)}
多项式 时切线的公式。英国的巴罗 、荷兰的于德 (Johnann Van Waveren Hudde)和瓦隆 的斯卢兹 (René Francoiss Walther de Sluze)继续了费马的工作[ 7] [ 5]
1660年代,英国人伊萨克·牛顿 提出了“流数”的概念。牛顿在写于1671年的《流数法与无穷级数》中对流数的解释是:“我把时间看作是连续的流动或增长,而其他的量则随着时间而连续增长。我从时间流动性出发,把所有其他量的增长速度称为流数。”也就是说,流数就是导数。牛顿将无穷小的时间间隔定义为“瞬间”(moment),而一个量的增量则是流数与瞬间的乘积。求导数时,牛顿将自变量和因变量两边展开,同时除以瞬间,再将剩下的项中含有瞬间的项忽略掉[ 6] :72 。而在他的第三篇微积分论文中,牛顿使用了新的概念:最初比和最后比。他说:
“
随我们的意愿,流数可以任意地接近于在尽可能小的等间隔时段中产生的增量,精确地说,它们是最初增量的最初的比,它们也能用和它们成比例的任何线段来表示。[ 6] :74
”
相比于牛顿,德国数学家莱布尼兹 使用了更清晰的记号来描述导数(见导数的记法 一节)。他利用了巴罗的“微分三角形”概念,将自变量和因变量的增量记为
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
x
{\displaystyle x}
y
{\displaystyle y}
[ 6] :89 。而导数则是两者之间的比例。他还研究了函数之和、差、积、商的求导法则。
伊萨克·牛顿爵士 牛顿和莱布尼兹的差别在于,牛顿将无穷小量作为求流数或导数的工具,而莱布尼兹则用无穷小量的比值来表示导数。这与二人的哲学思想差异有关[ 6] :92 。
微积分的理论面世后,遭到了有关无穷小量定义的攻击与质疑。导数的定义自然也包括在内。莱布尼兹和牛顿对无穷小量的认识都是模糊的。不仅如此,莱布尼兹甚至引入了
(
d
)
x
{\displaystyle (d)x}
(
d
)
y
{\displaystyle (d)y}
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
[ 6] :102 。
许多数学家,包括伯努利兄弟、泰勒 、麦克劳林 、达朗贝尔 、拉格朗日 和欧拉 都想要对微积分的严密性辩护或将微积分严密化。但受限于对无穷小量的认识,十八世纪的数学家并没有做出太大的成果。微积分的强烈抨击者,英国的乔治·贝克莱 主教在攻击无穷小量时认为,流数实际上是“消失的量的鬼魂”,是0与0之比。欧拉承认后者,并认为0与0之比可以是有限值。拉格朗日则假定函数都可以展开为幂级数 ,并在此基础上定义导数[ 6] :154-156 。
十九世纪后,随着对函数连续性和极限的更深刻认识,微积分终于趋于严谨。波尔查诺 是首先将导数定义为函数值的改变量与自变量增量之比在自变量增量无限接近0时趋向的量。波尔查诺强调导数不是0与0之比,而是前面的比值趋向的数[ 8] :10 。柯西 在他的著作《无穷小分析教程概论》中也使用了同样的定义,并定义
d
y
{\displaystyle dy}
d
x
{\displaystyle dx}
[ 8] :11 。
从微积分发轫至如今,不同的数学家都曾使用过不同的记号来表示函数的导数。部分记号至今仍然使用,成为现代的通用记法。
作为微积分的发明人之一,牛顿 在1704年著作中将导数用函数符号上方的点来表示。例如
y
=
f
(
x
)
{\displaystyle y=f(x)}
y
˙
{\displaystyle {\dot {y}}}
y
¨
{\displaystyle {\ddot {y}}}
[ 9] :193-196 。他以后的数学家也会将
y
˙
{\displaystyle {\dot {y}}}
微分 。牛顿的记法中没有明确自变量,因此
y
{\displaystyle y}
x
{\displaystyle x}
y
′
:
x
′
{\displaystyle y':x'}
y
{\displaystyle y}
x
{\displaystyle x}
t
{\displaystyle t}
[ 9] :196 。而这个导数比(使用莱布尼兹的记号):
y
′
:
x
′
=
d
y
d
t
:
d
x
d
t
=
d
y
d
x
{\displaystyle y':x'={\frac {dy}{dt}}:{\frac {dx}{dt}}={\frac {dy}{dx}}}
牛顿的记号多见于物理学或与之有关的方面,如微分方程 中。以及直到现在,使用函数符号上加一点来表示某一变量的变化率(即对时间的导数)依然常见于各类物理学教材中(如使用
v
˙
{\displaystyle {\dot {v}}}
加速度 等)。注意到对于高阶的导数,这种记法就无法表示了。
戈特弗里德·威廉·莱布尼茨 莱布尼兹 在他的研究中分别使用
Δ
x
{\displaystyle \Delta x}
Δ
y
{\displaystyle \Delta y}
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
无穷小量 ”)[ 10]
y
=
f
(
x
)
{\displaystyle y=f(x)}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
d
f
d
x
(
x
)
{\displaystyle {\frac {df}{dx}}(x)}
d
d
x
f
(
x
)
{\displaystyle {\frac {d}{dx}}f(x)}
d
(
f
(
x
)
)
d
x
,
{\displaystyle {\frac {d\left(f(x)\right)}{dx}},}
这个记法最早出现在莱布尼兹1684年的论文中[ 9] :204 ,莱布尼兹在之前的文章中会将
d
x
{\displaystyle dx}
x
d
{\displaystyle {\tfrac {x}{d}}}
d
y
d
x
{\displaystyle {\tfrac {dy}{dx}}}
d
y
x
{\displaystyle d{\tfrac {y}{x}}}
[ 11]
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
d
y
{\displaystyle dy}
d
x
{\displaystyle dx}
[ 10]
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
x
=
a
{\displaystyle x=a}
d
y
d
x
|
x
=
a
{\displaystyle \left.{\frac {dy}{dx}}\right|_{x=a}}
n 阶,见高阶导数 一节),莱布尼兹的记法是:
d
n
y
d
x
n
{\displaystyle {\frac {d^{n}y}{dx^{n}}}}
d
n
f
d
x
n
(
x
)
{\displaystyle {\frac {d^{n}f}{dx^{n}}}(x)}
d
n
[
f
(
x
)
]
d
x
n
,
{\displaystyle {\frac {d^{n}\left[f(x)\right]}{dx^{n}}},}
这种记法是在1695年出现的[ 9] :205 。这里的分子和分母不再具有单独的意义。莱布尼兹的记法中使用
d
d
x
{\displaystyle {\frac {d}{dx}}}
d
2
y
d
x
2
{\displaystyle {\frac {d^{2}y}{dx^{2}}}}
d
2
y
d
x
2
=
d
d
x
(
d
y
d
x
)
{\displaystyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}\left({\frac {dy}{dx}}\right)}
[ 11] 莱布尼兹记法的另一个好处是便于记忆导数计算的法则。例如链式法则 (见导数的计算 一节)应用莱布尼兹的记法就是:
d
y
d
x
=
d
y
d
u
⋅
d
u
d
x
{\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}}
可以想象为右边是两个分式的乘积,消去
d
u
{\displaystyle du}
[ 11]
由于牛顿和莱布尼兹之间关于微积分创始人称号的持久纠纷,在十八世纪早期的很长时间里,英国数学界与欧洲大陆的数学界分别采用牛顿和莱布尼兹的记号,泾渭分明。这种情况直到十八世纪后期才开始改变,随着拉格朗日记法的出现而变得多样化起来[ 9] :197-200 。
另一种现今常见的记法是十八世纪拉格朗日 于1797年率先使用的,以在函数的右上角加上一短撇作为导数的记号。函数
y
=
f
(
x
)
{\displaystyle y=f(x)}
f
′
(
x
)
{\displaystyle f'(x)}
y
′
{\displaystyle y'}
[ 12]
f
″
(
x
)
{\displaystyle f''(x)}
y
″
{\displaystyle y''}
f
‴
(
x
)
{\displaystyle f'''(x)}
y
‴
{\displaystyle y'''}
[ 9] :207 。如果需要处理更高阶的导数,则用括号内的求导阶数n 来代替短撇,记为:
f
(
n
)
(
x
)
{\displaystyle f^{(n)}(x)}
y
(
n
)
{\displaystyle y^{(n)}}
柯西 处理微分学时,他认为莱布尼兹的记法“模糊不便”,而采用更为“紧凑”的记法,将
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
y
x
′
{\displaystyle y'_{x}}
[ 9] :218 。后来这种记法曾继续被精简为
y
x
{\displaystyle y_{x}}
[ 13]
十九世纪以前,尽管大部分数学家会选择采用牛顿、莱布尼兹或拉格朗日的记号来表示导数,但也有很多的数学家希望使用自己的方法来记录。在不同数学家的著作中可以看到各种主流记法的混合或变体。数学家之间关于什么样的记法最为简便和严谨也是各执一词。同时,由于函数的微分、导数、偏导数以及无穷小量等概念尚未成熟,记号的不统一更增加了数学家之间相互理解的难度[ 9] :214-234 。十九世纪初期的德国数学家马尔丹·欧姆 采用
∂
f
(
x
)
{\displaystyle \partial f(x)}
雅可比 则采用
∂
f
∂
x
{\displaystyle {\frac {\partial f}{\partial x}}}
d
f
d
x
{\displaystyle {\frac {df}{dx}}}
[ 14]
d
x
f
{\displaystyle {\frac {d}{x}}f}
[ 15]
δ
f
δ
x
{\displaystyle {\frac {\delta f}{\delta x}}}
[ 16]
用大写字母
D
{\displaystyle D}
路易斯·弗朗索瓦·安托内·阿伯加斯特 (Louis François Antoine Arbogast )使用
D
m
f
{\displaystyle D^{m}f}
f
{\displaystyle f}
全微分 [ 17] 本杰明·佩尔斯 也使用
D
f
⋅
x
{\displaystyle Df\cdot x}
f
{\displaystyle f}
x
{\displaystyle x}
[ 18]
D
x
m
f
{\displaystyle D_{x}^{m}f}
f
{\displaystyle f}
x
{\displaystyle x}
偏导数 [ 19]
如果一个函数 的定义域 为全体实数 ,即函数在
(
−
∞
,
+
∞
)
{\displaystyle (-\infty ,+\infty )}
f
{\displaystyle f}
符号函数 (sgn函数)是一个不连续的函数在断点处不可导的例子:
符号函数 首先注意到这个函数在
x
0
=
0
{\displaystyle x_{0}=0}
x
=
0
{\displaystyle x=0}
该函数在
x
0
=
0
{\displaystyle x_{0}=0}
f
(
x
)
−
f
(
x
0
)
x
−
x
0
=
−
1
−
0
x
−
0
=
−
1
x
{\displaystyle {\frac {f(x)-f(x_{0})}{x-x_{0}}}={\frac {-1-0}{x-0}}=-{\frac {1}{x}}}
当
x
→
0
−
{\displaystyle x\to 0^{-}}
x
0
=
0
{\displaystyle x_{0}=0}
然而,连续性并不能保证可导性。即使函数在一点上连续,也不一定就在这一点可导。事实上,存在着在每一点都连续,但又在每一点都不可导的“病态函数”。1931年,斯特凡·巴拿赫 甚至证明,事实上“绝大多数 ”的连续函数都属于这种病态函数(至少在一点可导的连续函数在所有连续函数中是贫集 )[ 20]
左导数:
f
−
′
(
x
0
)
=
lim
Δ
x
→
0
−
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
{\displaystyle f'_{-}(x_{0})=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}}
[ 2] :118 [ 1] :155
右导数:
f
+
′
(
x
0
)
=
lim
Δ
x
→
0
+
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
{\displaystyle f'_{+}(x_{0})=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}}
[ 2] :118 [ 1] :155
然而左导数和右导数并不相等,因而函数在该处不可导。实际上,若函数导数存在,则必然可以推出左右导数相等,这是由极限的性质(极限存在则左右极限相等)得来:
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
Δ
x
→
0
−
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
Δ
x
→
0
+
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
{\displaystyle \lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{-}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim _{\Delta x\to 0^{+}}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}}
下面以绝对值函数作为例子:
绝对值函数 该函数在
x
=
0
{\displaystyle x=0}
f
−
′
(
0
)
=
lim
x
→
0
−
f
(
x
)
−
f
(
0
)
x
−
0
=
lim
x
→
0
−
−
x
−
0
x
−
0
=
−
1
{\displaystyle f'_{-}(0)=\lim _{x\to 0^{-}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{-}}{\frac {-x-0}{x-0}}=-1}
该函数在
x
=
0
{\displaystyle x=0}
f
+
′
(
0
)
=
lim
x
→
0
+
f
(
x
)
−
f
(
0
)
x
−
0
=
lim
x
→
0
+
x
−
0
x
−
0
=
1
{\displaystyle f'_{+}(0)=\lim _{x\to 0^{+}}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\to 0^{+}}{\frac {x-0}{x-0}}=1}
绝对值函数在
x
=
0
{\displaystyle x=0}
x
=
0
{\displaystyle x=0}
[ 2] :118-119
如果函数在一点的左右导数都存在并且相等,那么函数在该处可导。[ 1] :155
通过认识可导函数的导数,可以推断出不少函数本身的性质。
x变化时函数
f
(
x
)
=
1
+
x
sin
(
x
2
)
{\displaystyle \scriptstyle f(x)=1+x\sin(x^{2})}
根据微积分基本定理 ,对于可导的函数
f
{\displaystyle f}
f
(
b
)
−
f
(
a
)
=
∫
a
b
f
′
(
t
)
d
t
{\displaystyle f(b)-f(a)=\int _{a}^{b}f'(t)\mathrm {d} t}
如果函数的导函数在某一区间内恒大于零(或恒小于零),那么函数在这一区间内单调递增(或单调递减),这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点 (或极值可疑点),在这类点上函数可能会取得极大值或极小值。进一步判断则需要知道导函数在附近的符号。对于满足
f
′
(
x
0
)
=
0
{\displaystyle f'(x_{0})=0}
x
0
{\displaystyle x_{0}}
δ
>
0
{\displaystyle \delta >0}
f
′
{\displaystyle f'}
(
x
0
−
δ
,
x
0
]
{\displaystyle (x_{0}-\delta ,x_{0}]}
[
x
0
,
x
0
+
δ
)
{\displaystyle [x_{0},x_{0}+\delta )}
x
0
{\displaystyle x_{0}}
[ 2] :170 。如果
f
″
(
x
0
)
=
0
{\displaystyle f''(x_{0})=0}
f
″
(
x
)
{\displaystyle f''(x)}
x
0
{\displaystyle x_{0}}
拐点 ;否则这个点不是拐点 。[ 21] :200
如果函数在
x
0
{\displaystyle x_{0}}
f
″
(
x
0
)
{\displaystyle f''(x_{0})}
f
′
(
x
0
)
=
0
{\displaystyle f'(x_{0})=0}
f
″
(
x
0
)
>
0
{\displaystyle f''(x_{0})>0}
x
0
{\displaystyle x_{0}}
[ 2] :170-171 。
可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增,那么这个区间上函数是向下凸的,反之则是向上凸的。如果二阶导函数存在,也可以用它的正负性判断,如果在某个区间上
f
″
{\displaystyle f''}
[ 2] :176-178 。
原则上,函数的导数可以通过考虑差商 和计算其极限 来从定义计算。在实践中,一旦知道了一些简单函数的导数,就可以使用从更简单的函数获得更复杂函数的导数的规则,来更容易地计算其他函数的导数。
所谓基本函数是指一些形式简单并且容易求出导数的函数。这些基本函数的导函数可以通过定义直接求出。
f
(
x
)
=
x
r
,
{\displaystyle f(x)=x^{r},}
其中
r
{\displaystyle r}
f
′
(
x
)
=
r
x
r
−
1
,
{\displaystyle f'(x)=rx^{r-1},}
f
{\displaystyle f}
实数 域,但导函数的定义域 则不一定与之相同。例如当
r
=
1
2
{\displaystyle r={\frac {1}{2}}}
f
′
(
x
)
=
1
2
x
−
1
2
{\displaystyle f'(x)={\frac {1}{2}}x^{-{\tfrac {1}{2}}}\,}
[ 2] :119 导函数的定义域只限所有正实数而不包括0。需要注意的是,不会有多项式函数的导数为
x
−
1
{\displaystyle \scriptstyle x^{-1}}
r
=
0
{\displaystyle r=0}
底数为
e
{\displaystyle e}
指数函数
y
=
e
x
{\displaystyle \scriptstyle y=e^{x}}
d
d
x
e
x
=
e
x
.
{\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}.}
y
=
a
x
{\displaystyle y=a^{x}}
d
d
x
a
x
=
ln
(
a
)
a
x
.
{\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}a^{x}=\ln(a)a^{x}.}
[ 2] :122 自然对数函数 的导数则是
x
−
1
{\displaystyle x^{-1}}
d
d
x
ln
(
x
)
=
1
x
,
x
>
0.
{\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}},\qquad x>0.}
[ 2] :123 同样的,一般的对数函数导数则还需要乘以一个系数:
d
d
x
log
a
(
x
)
=
1
x
ln
(
a
)
{\displaystyle \scriptstyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{a}(x)={\frac {1}{x\ln(a)}}}
d
d
x
sin
(
x
)
=
cos
(
x
)
.
{\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x).}
d
d
x
cos
(
x
)
=
−
sin
(
x
)
.
{\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x).}
d
d
x
tan
(
x
)
=
sec
2
(
x
)
=
1
cos
2
(
x
)
=
1
+
tan
2
(
x
)
.
{\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x).}
d
d
x
cot
(
x
)
=
−
csc
2
(
x
)
=
−
1
sin
2
(
x
)
.
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\cot(x)=-\csc ^{2}(x)=-{\frac {1}{\sin ^{2}(x)}}.}
d
d
x
arcsin
(
x
)
=
1
1
−
x
2
,
−
1
<
x
<
1.
{\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}
d
d
x
arccos
(
x
)
=
−
1
1
−
x
2
,
−
1
<
x
<
1.
{\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}},\qquad -1<x<1.}
d
d
x
arctan
(
x
)
=
1
1
+
x
2
{\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下:
求导的线性性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合。
(
a
f
+
b
g
)
′
=
a
f
′
+
b
g
′
{\displaystyle (af+bg)'=af'+bg'\,}
a
,
b
{\displaystyle a,b}
[ 2] :121 两个函数的乘积的导函数,等于其中一个的导函数乘以另一者,加上另一者的导函数与其的乘积
(
f
g
)
′
=
f
′
g
+
f
g
′
{\displaystyle (fg)'=f'g+fg'\,}
[ 2] :125 两个函数的商的导函数也是一个分式。其中分子是分子函数的导函数乘以分母函数减去分母函数的导函数乘以分子函数后的差,而其分母是分母函数的平方。
(
f
g
)
′
=
f
′
g
−
f
g
′
g
2
{\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}
g
(
x
)
≠
0
{\displaystyle g(x)\neq 0}
[ 2] :126 复合函数的求导法则 :如果有复合函数
f
(
x
)
=
h
[
g
(
x
)
]
{\displaystyle f(x)=h[g(x)]}
f
′
(
x
)
=
h
′
[
g
(
x
)
]
⋅
g
′
(
x
)
.
{\displaystyle f'(x)=h'[g(x)]\cdot g'(x).\,}
[ 2] :128 若要求某个函数在某一点的导数,可以先运用以上方法求出这个函数的导函数,再看导函数在这一点的值。
欲求函数
f
(
x
)
=
x
4
+
sin
(
x
2
)
−
ln
(
x
)
e
x
+
7
{\displaystyle f(x)=x^{4}+\sin(x^{2})-\ln(x)e^{x}+7\,}
在
x
=
3
{\displaystyle x=3}
f
′
(
x
)
=
4
x
(
4
−
1
)
+
d
(
x
2
)
d
x
cos
(
x
2
)
−
[
d
(
ln
x
)
d
x
e
x
+
ln
x
d
(
e
x
)
d
x
]
+
0
=
4
x
3
+
2
x
cos
(
x
2
)
−
1
x
e
x
−
ln
(
x
)
e
x
.
{\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {\mathrm {d} \left(x^{2}\right)}{\mathrm {d} x}}\cos(x^{2})-\left[{\frac {\mathrm {d} \left(\ln {x}\right)}{\mathrm {d} x}}e^{x}+\ln {x}{\frac {\mathrm {d} \left(e^{x}\right)}{\mathrm {d} x}}\right]+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}
其中第二项使用了复合函数的求导法则,而第三项则使用了乘积的求导法则。求出导函数后,再将
x
=
3
{\displaystyle x=3}
f
′
(
3
)
=
108
+
6
cos
(
9
)
−
e
3
3
−
ln
(
3
)
e
3
{\displaystyle f'(3)=108+6\cos(9)-{\frac {e^{3}}{3}}-\ln(3)e^{3}\,}
如果函数的导数
f
′
(
x
)
{\displaystyle f'(x)\,}
x
{\displaystyle x\,}
[
f
′
(
x
)
]
′
{\displaystyle [f'(x)]'\,}
x
{\displaystyle x\,}
f
″
(
x
)
{\displaystyle f''(x)\,}
y
″
{\displaystyle y''\,}
d
2
y
d
x
2
{\displaystyle {\frac {{\rm {d}}^{2}y}{{\rm {d}}x^{2}}}}
d
2
f
(
x
)
d
x
2
{\displaystyle {\frac {{\rm {d}}^{2}f(x)}{{\rm {d}}x^{2}}}}
[ 2] :132 、
二阶导数可用于求解函数凹凸性问题。
f
″
(
x
)
>
0
{\displaystyle f''(x)>0}
f
″
(
x
)
<
0
{\displaystyle f''(x)<0}
二阶导数的导数称为三阶导数,记做
f
‴
(
x
)
{\displaystyle f'''(x)\,}
y
‴
{\displaystyle y'''\,}
d
3
y
d
x
3
{\displaystyle {\frac {{\rm {d}}^{3}y}{{\rm {d}}x^{3}}}}
d
3
f
(
x
)
d
x
3
{\displaystyle {\frac {{\rm {d}}^{3}f(x)}{{\rm {d}}x^{3}}}}
三阶导数的导数称为四阶导数,记做
f
(
4
)
(
x
)
{\displaystyle f^{(4)}(x)\,}
y
(
4
)
{\displaystyle y^{(4)}\,}
d
4
y
d
x
4
{\displaystyle {\frac {{\rm {d}}^{4}y}{{\rm {d}}x^{4}}}}
d
4
f
(
x
)
d
x
4
{\displaystyle {\frac {{\rm {d}}^{4}f(x)}{{\rm {d}}x^{4}}}}
一般的
f
(
x
)
{\displaystyle f(x)\,}
n
−
1
{\displaystyle n-1\,}
f
(
x
)
{\displaystyle f(x)\,}
n
{\displaystyle n\,}
f
(
n
)
(
x
)
{\displaystyle f^{(n)}(x)\,}
y
(
n
)
{\displaystyle y^{(n)}\,}
d
n
y
d
x
n
{\displaystyle {\frac {{\rm {d}}^{n}y}{{\rm {d}}x^{n}}}}
d
n
f
(
x
)
d
x
n
{\displaystyle {\frac {{\rm {d}}^{n}f(x)}{{\rm {d}}x^{n}}}}
[ 2] :133
一般来说,高阶导数的计算和导数一样,可以按照定义逐步求出。同时,高阶导数也有求导法则:
d
n
d
x
n
(
u
±
v
)
=
d
n
d
x
n
u
±
d
n
d
x
n
v
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\pm v)={\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\pm {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}v}
d
n
d
x
n
(
C
u
)
=
C
d
n
d
x
n
u
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(Cu)=C{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}u\ }
d
n
d
x
n
(
u
⋅
v
)
=
∑
k
=
0
n
C
k
n
d
n
−
k
d
x
n
−
k
u
d
k
d
x
k
v
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}(u\cdot v)=\sum _{k=0}^{n}C_{k}^{n}{\frac {{\rm {d}}^{n-k}}{{\rm {d}}x^{n-k}}}u{\frac {{\rm {d}}^{k}}{{\rm {d}}x^{k}}}v}
莱布尼兹公式 )[ 2] :134 因此,可以利用已知的高阶导数求导法则,通过四则运算, 变量代换等方法,求出
n
{\displaystyle n\ }
[ 2] :133 :
d
n
d
x
n
x
α
=
x
α
−
n
∏
k
=
0
n
−
1
(
α
−
k
)
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}x^{\alpha }=x^{\alpha -n}\prod _{k=0}^{n-1}(\alpha -k)}
d
n
d
x
n
1
x
=
(
−
1
)
n
n
!
x
n
+
1
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}{\frac {1}{x}}=(-1)^{n}{\frac {n!}{x^{n+1}}}}
d
n
d
x
n
ln
x
=
(
−
1
)
n
−
1
(
n
−
1
)
!
x
n
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\ln x=(-1)^{n-1}{\frac {(n-1)!}{x^{n}}}}
{\displaystyle \!}
d
n
d
x
n
e
x
=
e
x
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}e^{x}=e^{x}\ }
d
n
d
x
n
a
x
=
a
x
⋅
ln
n
a
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}a^{x}=a^{x}\cdot \ln ^{n}a}
(
a
>
0
)
{\displaystyle (a>0)\ }
{\displaystyle \!}
d
n
d
x
n
sin
(
k
x
+
b
)
=
k
n
sin
(
k
x
+
b
+
n
π
2
)
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\sin \left(kx+b\right)=k^{n}\sin \left(kx+b+{\frac {n\pi }{2}}\right)}
d
n
d
x
n
cos
(
k
x
+
b
)
=
k
n
cos
(
k
x
+
b
+
n
π
2
)
{\displaystyle {\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\cos \left(kx+b\right)=k^{n}\cos \left(kx+b+{\frac {n\pi }{2}}\right)}
当函数
y
{\displaystyle y}
R
n
{\displaystyle \mathbf {R} ^{n}}
向量 时,仍然可能对其求导。这时的函数值是:
y
=
(
y
1
(
x
)
,
y
2
(
x
)
,
⋯
,
y
n
(
x
)
)
{\displaystyle y=\left(y_{1}(x),y_{2}(x),\cdots ,y_{n}(x)\right)}
y
i
(
x
)
,
1
⩽
i
⩽
n
{\displaystyle y_{i}(x),\;\;1\leqslant i\leqslant n}
参数方程 。因此,对
y
=
f
(
x
)
{\displaystyle y=f(x)}
y
i
(
x
)
{\displaystyle y_{i}(x)}
y
′
(
t
)
=
(
y
1
′
(
t
)
,
⋯
,
y
n
′
(
t
)
)
.
{\displaystyle \mathbf {y} '(t)=(y'_{1}(t),\cdots ,y'_{n}(t)).}
[ 2] :191 这也符合定义
y
′
(
t
)
=
lim
h
→
0
y
(
t
+
h
)
−
y
(
t
)
h
,
{\displaystyle \mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},}
设
(
e
1
,
e
2
,
⋯
e
n
)
{\displaystyle \left(e_{1},e_{2},\cdots e_{n}\right)}
R
n
{\displaystyle \mathbf {R} ^{n}}
基 ,那么对函数:
y
:
t
↦
y
1
(
t
)
e
1
+
y
2
(
t
)
e
2
+
⋯
y
n
(
t
)
e
n
,
{\displaystyle y\,:t\,\mapsto \,y_{1}(t)e_{1}+y_{2}(t)e_{2}+\cdots y_{n}(t)e_{n},}
其导函数为:
y
′
(
t
)
=
y
1
′
(
t
)
e
1
+
y
2
′
(
t
)
e
2
+
⋯
y
n
′
(
t
)
e
n
{\displaystyle y'(t)=y'_{1}(t)e_{1}+y'_{2}(t)e_{2}+\cdots y'_{n}(t)e_{n}}
如果有函数
f
{\displaystyle f}
f
(
x
,
y
)
=
x
2
+
x
y
+
y
2
.
{\displaystyle f(x,y)=x^{2}+xy+y^{2}.\,}
这时可以把其中一个元素(比如
x
{\displaystyle x}
f
{\displaystyle f}
f
(
x
,
y
)
=
f
x
(
y
)
=
x
2
+
x
y
+
y
2
.
{\displaystyle f(x,y)=f_{x}(y)=x^{2}+xy+y^{2}.\,}
也就是说,对于某个确定的
x
{\displaystyle x}
f
x
{\displaystyle f_{x}}
y
{\displaystyle y}
x
=
a
{\displaystyle x=a}
f
x
{\displaystyle f_{x}}
y
{\displaystyle y}
f
a
′
(
y
)
=
a
+
2
y
{\displaystyle f_{a}'(y)=a+2y\,}
这个表达式对于所有的
a
{\displaystyle a}
∂
f
∂
y
(
x
,
y
)
=
x
+
2
y
{\displaystyle {\frac {\partial f}{\partial y}}(x,y)=x+2y}
这里的符号 ∂ 是字母
d
{\displaystyle d}
δ
{\displaystyle \delta }
d
{\displaystyle d}
更一般地来说,一个多元函数
f
(
x
1
,
x
2
,
⋯
,
x
n
)
{\displaystyle f\left(x_{1},x_{2},\cdots ,x_{n}\right)}
(
a
1
,
a
2
,
⋯
,
a
n
)
{\displaystyle \left(a_{1},a_{2},\cdots ,a_{n}\right)}
x
i
{\displaystyle x_{i}}
∂
f
∂
x
i
(
a
1
,
…
,
a
n
)
=
lim
h
→
0
f
(
a
1
,
…
,
a
i
+
h
,
…
,
a
n
)
−
f
(
a
1
,
…
,
a
n
)
h
.
{\displaystyle {\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{n})}{h}}.}
上面的极限中,除了
x
i
{\displaystyle x_{i}}
f
a
1
,
…
,
a
i
−
1
,
a
i
+
1
,
…
,
a
n
(
x
i
)
=
f
(
a
1
,
…
,
a
i
−
1
,
x
i
,
a
i
+
1
,
…
,
a
n
)
{\displaystyle f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})}
因此,按定义有:
d
f
a
1
,
…
,
a
i
−
1
,
a
i
+
1
,
…
,
a
n
d
x
i
(
a
i
)
=
∂
f
∂
x
i
(
a
1
,
…
,
a
n
)
.
{\displaystyle {\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).}
偏导数的实质仍然是一元函数的导数。[ 22] :56
多变量函数的一个重要的例子,是从
R
n
{\displaystyle \mathbf {R} ^{n}}
R
2
{\displaystyle \mathbf {R} ^{2}}
R
3
{\displaystyle \mathbf {R} ^{3}}
R
{\displaystyle \mathbf {R} }
标量值函数
f
(
x
1
,
x
2
,
⋯
,
x
n
)
{\displaystyle f\left(x_{1},x_{2},\cdots ,x_{n}\right)}
f
{\displaystyle f}
x
i
{\displaystyle x_{i}}
∂
f
∂
x
i
{\displaystyle {\frac {\partial f}{\partial x_{i}}}}
x
=
a
{\displaystyle x={\boldsymbol {a}}}
∇
f
(
a
)
=
[
∂
f
∂
x
1
(
a
)
,
…
,
∂
f
∂
x
n
(
a
)
]
{\displaystyle \nabla f({\boldsymbol {a}})=\left[{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}}),\ldots ,{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})\right]}
这个向量称为
f
{\displaystyle f}
a
{\displaystyle {\boldsymbol {a}}}
梯度
f
{\displaystyle f}
∇
f
{\displaystyle \nabla f}
a
{\displaystyle a}
∇
f
(
a
)
{\displaystyle \nabla f(a)}
向量场 。
方向导数是比偏导数更加广泛的概念。导数的本质是函数值增量与自变量增量之比的极限。在多元函数
f
{\displaystyle f}
δ
{\displaystyle {\boldsymbol {\delta }}}
f
(
x
0
+
t
δ
)
−
f
(
x
0
)
{\displaystyle f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})}
这个增量为关于
t
{\displaystyle t}
f
{\displaystyle f}
t
{\displaystyle t}
t
{\displaystyle t}
∂
f
∂
δ
(
x
0
)
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})}
∂
f
∂
δ
(
x
0
)
=
lim
t
→
0
f
(
x
0
+
t
δ
)
−
f
(
x
0
)
t
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {\delta }}}}({\boldsymbol {x}}_{0})=\lim _{t\to 0}{\frac {f({\boldsymbol {x}}_{0}+t{\boldsymbol {\delta }})-f({\boldsymbol {x}}_{0})}{t}}}
方向导数表示了函数从某点开始在某个方向上的变化率。[ 22] :55-56
在
R
n
{\displaystyle \mathbf {R} ^{n}}
δ
{\displaystyle {\boldsymbol {\delta }}}
(
e
1
,
e
2
,
⋯
,
e
n
)
{\displaystyle \left({\boldsymbol {e}}_{1},{\boldsymbol {e}}_{2},\cdots ,{\boldsymbol {e}}_{n}\right)}
e
i
{\displaystyle {\boldsymbol {e}}_{i}}
x
i
{\displaystyle {\boldsymbol {x}}_{i}}
[ 22] :55-56
导数的概念建立在变量为实数之上,但也可以推广到更加广泛的意义上。推广的导数本质上仍旧是函数在局部一点上的线性逼近。
对于变量为复数的函数,也可以定义导数的概念。假设有复变函数
f
:
Ω
∈
C
→
C
{\displaystyle f:\Omega \in \mathbb {C} \to \mathbb {C} }
f
{\displaystyle f}
z
0
{\displaystyle z_{0}}
lim
z
→
z
0
f
(
z
)
−
f
(
z
0
)
z
−
z
0
{\displaystyle \lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}}
存在,那么就说函数
f
{\displaystyle f}
z
0
{\displaystyle z_{0}}
z
→
z
0
{\displaystyle z\to z_{0}}
z
−
z
0
{\displaystyle z-z_{0}}
模长 趋向于0。如果将复变量
z
{\displaystyle z}
x
+
i
y
{\displaystyle x+iy}
f
{\displaystyle f}
R
2
{\displaystyle \mathbb {R} ^{2}}
f
{\displaystyle f}
R
2
{\displaystyle \mathbb {R} ^{2}}
f
{\displaystyle f}
柯西-黎曼条件 满足的时候才能保证复变函数的复可导性[ 23]
在分布理论 里,弱微分的概念使得对更多严格意义上无法求导的函数也可以定义导函数。设
u
{\displaystyle u}
L
l
o
c
1
(
R
)
{\displaystyle L_{loc}^{1}(\mathbb {R} )\ }
v
∈
L
l
o
c
1
(
R
)
{\displaystyle v\in L_{loc}^{1}(\mathbb {R} )}
u
{\displaystyle u}
φ
{\displaystyle \varphi }
∫
R
u
(
t
)
φ
′
(
t
)
d
t
=
−
∫
R
v
(
t
)
φ
(
t
)
d
t
{\displaystyle \int _{\mathbb {R} }u(t)\varphi '(t)dt=-\int _{\mathbb {R} }v(t)\varphi (t)dt}
成立。其中测试函数是指紧支撑 的光滑函数 [ 24]
过
x
0
{\displaystyle x_{0}}
在凸分析 ,也就是对凸函数 的研究中,可以定义凸函数的次导数。次导数的概念是导数的几何意义的推广。由于函数是凸的,过它的图像上每一点总可以作一条直线,使得函数的图像在直线上方。这种直线的斜率称为函数在这点的次导数。如果函数在某点可导,那么次导数只有一个,等于其导数。如果函数像绝对值函数一样在零点有突然的转折,那么次导数可能不止一个。比如过零点而斜率在
(
−
1
,
1
)
{\displaystyle (-1,1)}
(
−
1
,
1
)
{\displaystyle (-1,1)}
[ 25]
早在十九世纪,在数学家明确了求导与积分的互逆关系以后,就出现了负阶次导数的记号:
D
−
n
=
∫
n
{\displaystyle D^{-n}=\int ^{n}}
[ 9] :208 。而非整数阶导数的概念则进一步将其推广。比如,半微分算子
H
=
D
1
2
{\displaystyle H=D^{\frac {1}{2}}}
H
2
(
f
)
(
x
)
=
H
[
H
(
f
)
]
(
x
)
=
D
(
f
)
(
x
)
=
f
′
(
x
)
{\displaystyle H^{2}(f)(x)=H[H(f)](x)=D(f)(x)=f'(x)}
定义非整数阶导数的方法不止一种,最常用的非整数阶导数定义为黎曼-刘维尔定义:
设
0
<
s
<
1
{\displaystyle 0<s<1}
f
{\displaystyle f}
D
t
−
s
f
(
t
)
=
1
Γ
(
s
)
∫
a
t
(
t
−
u
)
s
−
1
f
(
u
)
d
(
u
)
{\displaystyle D_{t}^{-s}f(t)={\frac {1}{\Gamma (s)}}\int _{a}^{t}(t-u)^{s-1}f(u)d(u)}
而对
n
−
1
<
β
<
n
{\displaystyle n-1<\beta <n}
f
{\displaystyle f}
β
{\displaystyle \beta }
D
t
β
f
(
t
)
=
d
n
d
t
n
[
D
t
−
n
−
β
f
(
t
)
]
{\displaystyle D_{t}^{\beta }f(t)={\frac {d^{n}}{dt^{n}}}\left[D_{t}^{-n-\beta }f(t)\right]}
[ 26] [ 27] 方向导数在无穷维向量空间如巴拿赫空间 和弗雷歇空间 上可以推广为加托导数 和弗雷歇导数 。二者都经常用于形式化泛函导数 的概念,常见于物理学,特别是量子场论 [ 28]
微分代数 中有导子的概念。导子是具备了微分算子的某些特征的运算子,例如向量场的李导数 ,或非交换代数中的交换子 [ 29] 域
R
{\displaystyle \mathbf {R} }
A
{\displaystyle {\mathcal {A}}}
A
{\displaystyle {\mathcal {A}}}
R
{\displaystyle \mathbf {R} }
δ
{\displaystyle \delta }
A
{\displaystyle {\mathcal {A}}}
R
{\displaystyle \mathbf {R} }
线性映射 (线性自同态),并满足导数的乘积法则:
δ
(
a
b
)
=
(
δ
a
)
b
+
a
(
δ
b
)
{\displaystyle \delta (ab)=(\delta a)b+a(\delta b)}
所有
R
{\displaystyle \mathbf {R} }
A
{\displaystyle {\mathcal {A}}}
End
A
{\displaystyle \operatorname {End} {\mathcal {A}}}
[ 30]
物理学 、几何学 、工程科学 、经济学 等学科中的一些重要概念都可以用导数来表示。如,导数可以表示运动物体的瞬时速度 和加速度 ,也可以表示曲线在一点的斜率 。
经济学中,所谓边际 和弹性 的概念与导数紧密相关。比如边际成本就是产量增加一个单位所带来的成本的增加,若将其连续化,得到的便是成本函数的导数。又如需求 的弹性是指价格变化一个单位时,需求量的变化,连续化后相应的也是需求函数关于价格的导数。[ 31]
^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 徐森林; 薛春华. 《数学分析(第一册)》. 清华大学出版社. 2005. ISBN 978-7-302-11746-9 ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 欧阳光中; 姚允龙; 周渊 (编). O.305. 《数学分析(上册)》. 复旦大学出版社. 2003. ISBN 7-309-03570-4 ^ 朝嵩金, 正敏段, 汉明王. 《线性代数》. 清华大学出版社. 2006. ISBN 7-302-12350-0 ^ 梁子杰. 「可微」還是「可導」? (PDF) . 数学教育. [永久失效链接 ^ 5.0 5.1 (英文) Dan Ginsburg, Brian Groose, Josh Taylor, Bogdan Vernescu. History of the Differential from the 17th Century . [2011-02-10 ] . (原始内容存档 于2021-02-18). ^ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 (中文) 莫里斯·克莱因 . 《古今数学思想》第二卷 . 由张理京、张锦炎、江泽涵 翻译. 上海科学技术出版社. 2002. ISBN 7-5323-6172-1 ^ (英文) W. W. Rouse Ball. Isaac Barrow [2011-02-10 ] . (原始内容存档 于2012-05-03). ^ 8.0 8.1 (中文) 莫里斯·克莱因 . 《古今数学思想》第四卷 . 由张理京、张锦炎、江泽涵 翻译. 上海科学技术出版社. 2002. ISBN 7-5323-6172-1 ^ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 Florian Cajori. A History of Mathematical Notations 第2卷 . Dover Publications. 1993年12月. ISBN 978-0486677668 ^ 10.0 10.1 Stewart, James. Calculus: Early Transcendentals 6th. Brooks/Cole . 2008. ISBN 0-495-01166-5 ^ 11.0 11.1 11.2 Mary Barnes. More about Functions and Differentiation. Curriculum Press. 1993. ^ (英文) The Notation of Differentiation . 1998-08-24 [2011-02-10 ] . (原始内容存档 于2017-12-05). ^ George Shoobridge Carr. A Synopsis of Elementary Results in Pure and Applied Mathematics . C. F. Hodgson. 1880. ^ M.Fontaine, Mémoires donnés à l'académie royale des sciences, non imprimés dans leur temps ,1764.
^ A. L. Crelle, Rechnungmit veranderlichcn GriJsscn , Vol. I (Gottingen, 1813).
^ Hamilton, Philosophical Transactions of the Royal Society ,(London, 1834), p.249
^ Louis François Antoine Arbogast, Calcul des Derivations , (1800), p.89
^ Benjamin Peirce, Elementary Treatise on Curves, Functions, and Forces (new ed. Boston and Cambridge), Vol I (1852)
^ (法文) A.L.Cauchy, Exercices d'analyse et de physique mathematique , (1844), p.12-17.^ Banach, S., Uber die Baire'sche Kategorie gewisser Funktionenmengen, Studia. Math., 1931, (3): 174–179. ^ Jon Rogawski. Single Variable Calculus. W. H. Freeman. 11 June 2007. ISBN 978-1-4292-1071-3 ^ 22.0 22.1 22.2 徐森林; 薛春华. 《数学分析(第二册)》. 清华大学出版社. 2005. ISBN 978-7-302-13141-0 ^ 郑建华. 《复变函数》. 清华大学出版社. 2005. ISBN 978-7302096931 ^ Evans, Lawrence C. Partial differential equations . Providence, R.I.: American Mathematical Society. 1998: 242 . ISBN 0-8218-0772-2 ^ (英文) Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal. Fundamentals of Convex Analysis ISBN 3-540-42205-6 ^ (中文) 薛定宇,陈阳泉. 《高等应用数学问题的MATLAB求解》. 清华大学出版社. 2004. ISBN 978-7302186182 ^
Igor Podlubny. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications. , (Mathematics in Science and Engineering, vol. 198). Academic Press. 1998年10月. ISBN 0-12-558840-2
^ (法文) R Gâteaux. Sur les fonctionnelles continues et les fonctionnelles analytiques (PDF) . Bulletin de la S.M.F, tome 50 (1922). [2011-02-11 ] . (原始内容存档 (PDF) 于2013-10-20). ^ Nicolas Bourbaki. Algebra I. Springer-Verlag. 1989. ISBN 3-540-64243-9 ^ Nathan Jacobson. Lie algebras ISBN 978-0486638324 ^ 翁秉仁. 經濟學應用:邊際與彈性 . EpisteMath,改写自同作者的《微积分讲义》. [2011-02-10 ] . (原始内容存档 于2020-12-21).



































































































![{\displaystyle {\frac {d^{n}\left[f(x)\right]}{dx^{n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/548759861ef6ddb81aa9f7ab786387011003f088)








































![{\displaystyle (x_{0}-\delta ,x_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9fd97a6ff2bf4cdaf1b0cddd124633d8522fff6)
































![{\displaystyle f(x)=h[g(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1eaf3599db95f07d69b7636228d096bb0e2c587)
![{\displaystyle f'(x)=h'[g(x)]\cdot g'(x).\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/138168bb43f9b39634758bd0d93b61fec74146f3)


![{\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {\mathrm {d} \left(x^{2}\right)}{\mathrm {d} x}}\cos(x^{2})-\left[{\frac {\mathrm {d} \left(\ln {x}\right)}{\mathrm {d} x}}e^{x}+\ln {x}{\frac {\mathrm {d} \left(e^{x}\right)}{\mathrm {d} x}}\right]+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfcbb452ee8159a43b9ad9b5b8f2b2dc351d4a35)



![{\displaystyle [f'(x)]'\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e876a3d7c8c80f07bb943d63f485245ee93a6b9)





























































![{\displaystyle \nabla f({\boldsymbol {a}})=\left[{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}}),\ldots ,{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3057452b1934ea1608a94e3a16c7b6016a2b2bb)


























=D(f)(x)=f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c816462a352c228015360fe442fcd7d4f2ae3c9e)




![{\displaystyle D_{t}^{\beta }f(t)={\frac {d^{n}}{dt^{n}}}\left[D_{t}^{-n-\beta }f(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d9d97b1f03c0faf5a6c4891fe2c7057767477ca)


