重积分

该积分是两条曲线之间的面积。

作为曲面下的体积的双重积分。该体积底部的矩形区域是积分的域，而曲面是被积的双变量函数的图像。

多重积分是定积分的一类，它将定积分扩展到多元函数（多变量的函数），例如求$f(x,y)$或者$f(x,y,z)$类型的多元函数的积分。

简介

正如单参数的正函数的定积分代表函数图像和x轴之间区域的面积一样，正的双变量函数的双重积分代表函数所定义的曲面和包含函数定义域的平面之间所夹的区域的体积。（注意同样的体积也可以通过三变量常函数f(x, y, z) = 1在上述曲面和平面之间的区域中的三重积分得到。若有更多变量，则多维函数的多重积分给出超体积。

n元函数f(x₁, x₂,…, x_n)在定义域D上的多重积分通常用嵌套的积分号按照演算的逆序标识（最左边的积分号最后计算），后面跟着被积函数和正常次序的积分参数（最右边的参数最后使用）。积分域或者对每个积分参数在每个积分号下标识，或者用一个变量标在最右边的积分号下：

$\int \ldots \int_\mathbf{D}\;f(x_1,x_2,\ldots,x_n) \;\mathrm{d}x_1 \!\ldots\mathrm{d}x_n$

因为不可能计算多于一个变量的函数的不定积分，不定多重积分是不存在的。因此所有多重积分都是定积分。

范例

譬如，边长为4 × 6 × 5的长方体的体积可以通过两种方法得到：

• 通过函数f(x, y) = 5在xy平面中的区域D，也就是长方体的底上的双重积分

$\iint_D 5 \ dx\, dy$

• 或者是常函数1在长方体上的三重积分

$\iiint_\mathrm{} 1 \, dx\, dy\, dz$

数学定义

令n为大于1的自然数。考虑所谓的半开n维矩形（下面简称矩形）。对于平面，n = 2，而多重积分就是双重积分。

$T=[a_1, b_1)\times [a_2, b_2)\times\cdots \times [a_n, b_n)\subset \mathbb R^n$。

将每个区间[a_i, b_i)分成有限个不重叠的子区间，每个都是左闭右开。将子区间记为I_i。则，所有所有如下形式的子矩形的族

$C=I_1\times I_2\times \cdots\times I_n$

是T的一个划分，也即，子矩形C是互不重叠的，而且它们并集为T。C中的子矩形的直径按照定义是C中最大的边长，而T的划分的直径就是划分中的子矩形的最大直径。

令f : T → R为定义在T上的函数。考虑如上定义的T的划分

$T=C_1\cup C_2\cup \cdots \cup C_m$

其中m是正整数。如下形式的和称为黎曼和

$\sum_{k=1}^m f(P_k)\, \operatorname{m}(C_k)$

其中，对于每个k，点P_k在C_k中，而m(C_k)是笛卡尔积为C_k的区间的边长之积。

函数f称为黎曼可积，如果如下极限存在

$S = \lim_{\delta \to 0} \sum_{k=1}^m f(P_k)\, \operatorname{m}\, (C_k)$

其中极限取遍所有直径最大为δ的T的划分。若f黎曼可积，S称为f在T上的黎曼积分。记为

$\int_T\!f(x)\,dx$。

定义在任意有界n维集合上的函数的黎曼和可以通过将函数延拓到一个半开半闭矩形上来求出，其取值在原来的定义域之外为0。然后，原来的函数的积分就定义为延展的函数在矩形区域中的积分（如果存在的话）。

下文中n维黎曼积分简称多重积分。

性质

多重积分具有很多与单变量函数的积分一样的性质（线性，可加性，单调性，等等）。而且，和单变量情况一样，可以用多重积分找出函数在给定集合上的积分。具体来讲，给定集合D ⊆ Rⁿ和D上的可积函数f，f在定义域上的平均值为

$\bar{f} = \frac{1}{m(D)} \int_D f(x)\, dx,$

其中m（D）是D的测度。

特例

T ⊆ R²是，积分

$\ell = \iint_T f(x,y)\, dx\, dy$

是f在T上的双重积分，而若T ⊆ R³，积分

$\ell = \iiint_T f(x,y,z)\, dx\, dy\, dz$

是f在T上的三重积分。

注意，按常规，双重积分用两个积分号，而三重积分有三个；这只是记法上方便，也是为了通过重复积分来计算多重积分（参看本条目后文）。

积分方法

多重积分问题的解决在多数情况下依赖于将多重积分转化为一系列单变量积分，而其中每个单变量积分都是直接可解的。

直接检验

有时可以直接获得积分的结果，而无需任何直接计算。

常数

在常函数的情况中，结果很直接：只要将常函数c乘以测度就可以了。如果c = 1，而且是在R²的子集中积分，则乘积就是区域面积，而在R³中，它就是区域的体积。

• 例如：

$D = \{ (x,y) \in \mathbb{R}^2 \ : \ 2 \le x \le 4 \ ; \ 3 \le y \le 6 \}$ and $f(x,y) = 2\,\!$

在D上积分f：

$\int_3^6 \int_2^4 \ 2 \ dx\, dy = \mbox{area}(D) \cdot 2 = (2 \cdot 3) \cdot 2 = 12$。

利用可能的对称性

如果定义域存在沿着某条轴的对称性而且函数对于那个变量是奇函数，则积分为0（因为相反的两部分加起来为0）。

对于Rⁿ中的函数，只要相关变量对于形成对称的轴是奇变量就可以了。

• 例一:

给定f(x, y) = 2 sin x − 3y³ + 5以及T = x² + y² ≤ 1为积分区域（半径为1的圆盘，包含边界）。

利用线性性质，积分可以分解为三部分：

$\iint_T (2 \ \sin x - 3 \ y^3 + 5) \ dx \, dy = \iint_T 2 \ \sin x \ dx \, dy - \iint_T 3 \ y^3 \ dx \ dy + \iint_T 5 \ dx \ dy$

2  sin x和3y³都是奇函数，而且显然T对于x和y轴都是对称的；因此唯一有贡献的部分是常函数5因为其它两个都贡献0.

• 例二：

考虑函数f(x, y, z) = x   exp(y² + z²)以及圆心在原点的半径为2的球T = x² + y² + z² ≤ 4。该球显然是对于三条轴都对称，但是只要对于x轴积分就可以看出结果是0，因为f对于该变量是奇函数。

简化公式

简化公式基于简单积分区域来将多重积分转化为单变量积分的序列。它们必须从右至左计算，过程中将其它变量暂时视为常数（和偏导数的计算类似）。

R²中的常规区域

此種方法適用於滿足下述條件的任何定義域 D:

• D 投影到 x軸或 y軸任一軸，形成一個有邊界的範圍, 以 a, b 代表邊界值。
• 通過 a, b 兩點並與$\overline{ab}$ 垂直的直線與 D 相交後的兩個端點，可以用 2 個函數$\alpha$, $\beta$ 定義。

x轴

將 D 對 x軸做垂直投影，函數$f: D \longrightarrow \mathbb{R}$是连续函数，并且D可以视为（定义在[a,b]区间上的）α(x)和β(x)之间的区域。则

$\iint_D f(x,y)\ dx\, dy = \int_a^b dx \int_{ \alpha (x)}^{ \beta (x)} f(x,y)\, dy$

y轴

將 D對y軸做垂直投影，函數$f: D \longrightarrow \mathbb{R}$是连续函数，并且D可以视为（定义在[a,b]区间上的）α(y)和β(y)之间的区域。则

$\iint_D f(x,y)\ dx\, dy = \int_a^b dy \int_{ \alpha (y)}^{ \beta (y)} f(x,y)\, dx$

范例

例：可以采用简化公式的D区域。

考虑区域：$D = \{ (x,y) \ : \ x \ge 0, y \le 1, y \ge x^2 \}$（参看附图）。计算

$\iint_D (x+y) \, dx \, dy$

该区域可以沿x或者y轴分解。要采用公式，必须先找到限制D的两个函数和定义区间。

这个例子中，这两个函数为：

$\alpha (x) = x^2\,\!$ 和 $\beta (x) = 1\,\!$

而区间为$[a,b] = [0,1]\,\!$（这里为了直观起见采用沿x轴分解）。

应用简化公式，得到：

$\iint_D (x+y) \, dx \, dy = \int_0^1 dx \int_{x^2}^1 (x+y) \, dy = \int_0^1 dx \ \left[xy \ + \ \frac{y^2}{2} \ \right]^1_{x^2}$

（首先，第二个积分将x作为常数）。然后就是用积分的基本技术：

$\int_0^1 \left[xy \ + \ \frac{y^2}{2} \ \right]^1_{x^2} \, dx = \int_0^1 \left(x + \frac{1}{2} - x^3 - \frac{x^4}{2} \right) dx = \cdots = \frac{13}{20}$。

如果沿着y轴分解，可以计算

$\int_0^1 dy \int_0^{\sqrt{y}} (x+y) \, dx$

并得到同样的结果。

R3中可(沿xy平面）分解区域的例子。

R³中的分解

这些公式可以推广到三重积分：

T是一个可以投影到xy平面的体，它夹在α (x,y)和β(x,y)两个函数之间。那么：

$\iiint_T f(x,y,z) \ dx\, dy\, dz = \iint_D dx\, dy \int_{\alpha (x,y)}^{\beta (x,y)} f(x,y,z) \, dz$

（此定义和其它R³中的分解类似）。

变量替换

积分的极限常常不易交换（区域无法分解或者公式很复杂），这时可以采用变量替换来重写积分，令区域更加简易，从而可以用更简单的公式表达。为此，函数必须变换到新坐标系下。

例（1-a）:

函数为$f(x, y) = (x-1)^2 +\sqrt y$;

若采用替换$x' = x-1, \ y'= y \, \!$则$x = x' + 1, \ y=y' \,\!$

可以得到新函数$f_2(x,y) = (x')^2 +\sqrt y$.

• 对于定义域要进行类似处理，因为原来是采用变换前的变量表达的（本例中的x和y）。
• 微分dx和dy要通过包含被替换的变量对于新变量的偏微分的雅可比行列式来变换。（譬如，极坐标的微分变换）。

常用的变量替换有三种（R²中一种，R³中两种）；但是，更普遍的变换可以用同样的原理来发现。

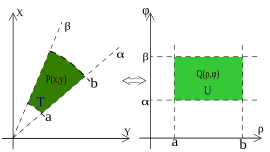
极坐标

从笛卡尔坐标系变换到极坐标系。

在R²中，若定义域有某种圆形对称性而函数也有某种特征，则可以采用极坐标变换（参看图中的例子），也就是说将点P(x,y)从笛卡尔坐标变换到相应的极坐标中。这使得定义域的形状改变，从而简化运算。

该变换的基本关系如下：

$f(x,y) \rightarrow f(\rho \ \cos \phi,\rho \ \sin \phi )$。

例（2-a）:

函数为$f(x,y) = x + y\,\!$

应用该变换得到

$f(\rho, \phi) = \rho \cos \phi + \rho \sin \phi = \rho \ (\cos \phi + \sin \phi )$。

例（2-b）:

函数为$f(x,y) = x^2 + y^2\,\!$

这裡有：

$f(\rho, \phi) = \rho^2 (\cos^2 \phi + \sin^2 \phi) = \rho^2\,\!$

这里使用了勾股定理（在简化操作时很有用）。

定义域的变换是根据x和y通过环厚和角度的幅度来限定ρ, φ的区间。

从笛卡尔到极坐标的区域变换。

例（2-c）:

区域为$D = x^2 + y^2 \le 4\,\!$，圆周半径2；很明显，这个区域所覆盖的角度是整个圆周角，所以φ从0变化到2π，而环半径从0变化到2（内环为0的环形就是圆）。

例（2-d）:

区域为$D = \{ x^2 + y^2 \le 9, \ x^2 + y^2 \ge 4, \ y \ge 0 \}$，这是在正y半平面中的圆环（参看示意图）；注意φ表示平面角而ρ从2变化到3。因此变换出来的区域为矩形：

$T = \{ 2 \le \rho \le 3, \ 0 \le \phi \le \pi \}$.

该变换的雅可比行列式为：

$\frac{\partial (x,y)}{\partial (\rho, \phi)} = \begin{vmatrix} \cos \phi & - \rho \sin \phi \\ \sin \phi & \rho \cos \phi \end{vmatrix} = \rho$

这可以通过将x = ρ cos(φ), y = ρ sin(φ)代入关于ρ的第一行和关于φ的第二行的偏微分中得到，所以微分dx dy变换为ρ dρ dφ.

一旦函数和区域的变换完成后，可以定义极坐标中的变量变换公式：

$\iint_D f(x,y) \ dx\, dy = \iint_T f(\rho \cos \phi, \rho \sin \phi) \rho \, d \rho\, d \phi$。

注意φ在[0, 2π]区间中有效，而ρ测量长度，因此只能取正值。

例 (2-e):

函数为$f(x,y) = x\,\!$区域和例2-d相同。

从前面对D的分析，我们知道ρ的区间为[2,3]，而φ的为[0,π].函数变换为：

$f(x,y) = x \longrightarrow f(\rho,\phi) = \rho \ \cos \phi$。

最后，应用积分公式：

$\iint_D x \, dx\, dy = \iint_T \rho \cos \phi \ \rho \, d\rho\, d\phi$。

一旦区间给定，就可以得到

$\int_0^{\pi} \int_2^3 \rho^2 \cos \phi \ d \rho \ d \phi = \int_0^{\pi} \cos \phi \ d \phi \left[ \frac{\rho^3}{3} \right]_2^3 = \left[ \sin \phi \right]_0^{\pi} \ \left(9 - \frac{8}{3} \right) = 0$。

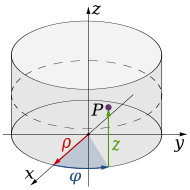
柱极坐标

柱极坐标。

R³中，在有圆形底面的定义域上的积分可以通过变换到柱极坐标系来完成；函数的变换用如下的关系进行：

$f(x,y,z) \rightarrow f(\rho \ \cos \phi,\rho \ \sin \phi, z)$

区域的变换可以从图形中得到，因为底面的形状可能不同，而高遵循初始区域的形状。

例（3-a）:

区域为$D = \{ x^2 + y^2 \le 9, \ x^2 + y^2 \ge 4, \ 0 \le z \le 5 \}$（也即底面为例2-d中的圆环的高度为5的"管道"）；如果采用变换，可以得到区域$T = \{ 2 \le \rho \le 3, \ 0 \le \phi \le \pi, \ 0 \le z \le 5 \}$（这是一个底面为例2-d中的矩形而高为5的长方体）。

因为z分量没有变化，dx dy dz和在极坐标中一样变化：变为ρ dρ dφ dz。

最后，变换到柱极坐标的最后公式为：

$\iiint_D f(x,y,z) \, dx\, dy\, dz = \iiint_T f(\rho \cos \phi, \rho \sin \phi, z) \rho \, d\rho\, d\phi\, dz$。

这个方法在柱形或者锥形区域的情况较为适用，也适用于容易分辨z区间和变换圆形底面和函数的其它情况。

例（3-b）:

函数为$f(x,y,z) = x^2 + y^2 + z\,\!$而积分区域为圆柱: $D = \{ x^2 + y^2 \le 9, \ -5 \le z \le 5 \}$.

将D变换到柱极坐标如下：

$T = \{ 0 \le \rho \le 3, \ 0 \le \phi \le 2 \pi, \ -5 \le z \le 5 \}$。

函数变为

$f(\rho \ \cos \phi,\rho \ \sin \phi, z) = \rho^2 + z\,\!$

最有应用积分公式：

$\iiint_D (x^2 + y^2 +z) \, dx\, dy\, dz = \iiint_T ( \rho^2 + z) \rho \, d\rho\, d\phi\, dz;$

推演一下公式，得到

$\int_{-5}^5 dz \int_0^{2 \pi} d\phi \int_0^3 ( \rho^3 + \rho z )\, d\rho = 2 \pi \int_{-5}^5 \left[ \frac{\rho^4}{4} + \frac{\rho^2 z}{2} \right]_0^3 \, dz$

$= 2 \pi \int_{-5}^5 \left( \frac{81}{4} + \frac{9}{2} z\right)\, dz = \cdots = 855 \pi$。

球极坐标

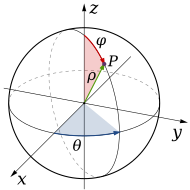
球极坐标。【注意某些地区（如北美）角度标识相反】

R³中，有些区域有球形对称性，所以将积分区域的每点用两个角度和一个距离标识较为合适。因此可以采用变换到球极坐标系；函数变换由如下关系产生：

$f(x,y,z) \longrightarrow f(\rho \cos \theta \sin \phi, \rho \sin \theta \sin \phi, \rho \cos \phi)\,\!$

注意z轴上的点没有唯一表示，$\theta$可以在0到2π间变化。

这个方法最为适用的区域显然是球。

例（4-a）:

区域为$D = x^2 + y^2 + z^2 \le 16$（球心在原点半径为4的球）；应用变换后得到：$T = \{ 0 \le \rho \le 4, \ 0 \le \phi \le \pi, \ 0 \le \theta \le 2 \pi \}$。

坐标变换的雅可比行列式为：

$\frac{\partial (x,y,z)}{\partial (\rho, \phi,\theta )} = \begin{vmatrix} \cos\theta \sin\phi & \rho \cos\theta \cos\phi & -\rho \sin\theta \sin\phi \\ \sin\theta \sin\phi & \rho \sin\theta \cos\phi & \rho \cos\theta \sin \phi \\ \cos\phi & -\rho \sin\phi & 0 \\ \end{vmatrix} = \rho^2 \sin \phi$

因此dx dy dz变换为ρ² sin(φ) dρ dθ dφ.

得到最后公式:

$\iiint_D f(x,y,z) \, dx\, dy\, dz = \iiint_T f(\rho \sin \theta \cos \phi, \rho \sin \theta \sin \phi, \rho \cos \theta) \rho^2 \sin \phi \, d\rho\, d\theta\, d\phi$。

应当在积分区域为球形对称并且函数很容易通过基本三角公式简化的时候才使用这个方法。（参看例4-b）；其它情况下，可能使用柱极坐标更为合适（参看例4-c）。

$\iiint_T f(a,b,c) \rho^2 \sin \phi \, d\rho\, d\theta\, d\phi$。

注意从雅可比行列式来的$\rho^2$和$\sin \phi$因子。

注意下面例子中，φ和θ的作用反过来了。

例（4-b）:

D和例4-a相同，而$f(x,y,z) = x^2 + y^2 + z^2\,\!$是被积函数。

很容易变换为：

$f(\rho \sin \theta \cos \phi, \rho \sin \theta \sin \phi, \rho \cos \theta) = \rho^2,$，

而从D到T的变换是已知的：

$(0 \le \rho \le 4, \ 0 \le \phi \le 2 \pi, \ 0 \le \theta \le \pi)$。

应用积分公式：

$\iiint_D (x^2 + y^2 +z^2) \, dx\, dy\, dz = \iiint_T \rho^2 \ \rho^2 \sin \theta \, d\rho\, d\theta\, d\phi,$

并展开：

$\iiint_T \rho^4 \sin \theta \, d\rho\, d\theta\, d\phi = \int_0^{\pi} \sin \theta \,d\theta \int_0^4 \rho^4 d \rho \int_0^{2 \pi} d\phi = 2 \pi \int_0^{\pi} \sin \theta \left[ \frac{\rho^5}{5} \right]_0^4 \, d \theta$

$= 2 \pi \left[ \frac{\rho^5}{5} \right]_0^4 \left[- \cos \theta \right]_0^{\pi} = 4 \pi \cdot \frac{1024}{5} = \frac{4096 \pi}{5}$。

例（4-c）:

区域D是球心在原点半径为3a的球（$D = x^2 + y^2 + z^2 \le 9a^2 \,\!$）而$f(x,y,z) = x^2 + y^2\,\!$是被积函数。

看起来采用球极坐标变换较为合适，但是事实上，限定新区域T的变量很明显应该是：

$0 \le \rho \le 3a, \ 0 \le \phi \le 2 \pi, \ 0 \le \theta \le \pi$。

但是采用这个变换就有

$f(x,y,z) = x^2 + y^2 \longrightarrow \rho^2 \sin^2 \theta \cos^2 \phi + \rho^2 \sin^2 \theta \sin^2 \phi = \rho^2 \sin^2 \theta$.

应用积分公式得到：

$\iiint_T \rho^2 \sin^2 \theta \rho^2 \sin \theta \, d\rho\, d\theta\, d\phi = \iiint_T \rho^4 \sin^3 \theta \, d\rho\, d\theta\, d\phi$

这很难求解。而如果采用柱极坐标，新的T区间为：

$0 \le \rho \le 3a, \ 0 \le \phi \le 2 \pi, \ - \sqrt{9a^2 - \rho^2} \le z \le \sqrt{9a^2 - \rho^2};$

z区间可以通过将球切成两个半球并求解从D的公式来的不等式得到（然后直接变换x² + y²到ρ²）。新函数就是ρ².采用积分公式

$\iiint_T \rho^2 \rho \ d \rho d \phi dz$.

得到

$\int_0^{2 \pi} d\phi \int_0^{3a} \rho^3 d\rho \int_{- \sqrt{9a^2 - \rho^2} }^{\sqrt{9 a^2 - \rho^2} }\, dz = 2 \pi \int_0^{3a} 2 \rho^3 \sqrt{9 a^2 - \rho^2} \, d\rho$。

然后应用变换

$9 a^2 - \rho^2 = t\,\! \longrightarrow dt = -2 \rho\, d\rho \longrightarrow d\rho = \frac{d t}{- 2 \rho}\,\!$

(新区间变为$0, 3a \longrightarrow 9 a^2, 0$)。得到

$- 2 \pi \int_{9 a^2}^{0} \rho^2 \sqrt{t}\, dt$

因为$\rho^2 = 9 a^2 - t\,\!$，所以

$-2 \pi \int_{9 a^2}^0 (9 a^2 - t) \sqrt{t}\, dt,$

将积分限反过来，然后分配括号中的项，很容易将积分分解为可以直接积分的两部分：

$2 \pi \left[ \int_0^{9 a^2} 9 a^2 \sqrt{t} \, dt - \int_0^{9 a^2} t \sqrt{t} \, dt\right] = 2 \pi \left[9 a^2 \frac{2}{3} t^{ \frac{3}{2} } - \frac{2}{5} t^{ \frac{5}{2}} \right]_0^{9 a^2}$

$= 2 \cdot 27 \pi a^5 ( 6 - \frac{2}{5} ) = 54 \pi \frac{28}{5} a^5 = \frac{1512 \pi}{5} a^5$。

由于采用柱极坐标，很容易就将这个三重积分变换为简单的单变量积分。

参看柱极和球极坐标下的∇中讨论的不同的体积元。

数学应用范例-体积计算

利用上面描述的方法，很容易计算一些立体的体积。

• 圆柱：半径为R的圆形底面作为定义域，将等于高度h的常函数作为积分对象。可以在极坐标中将体积写作：

体积$= \int_0^{2 \pi } d \phi \int_0^R h \rho \ d \rho = h 2 \pi \left[\frac{\rho^2}{2 }\right]_0^R = \pi R^2 h$

验证：体积=底面积×高 = $\pi R^2 \cdot h$

• 球:可以作为常函数1在球极坐标下的半径为R的球中积分：

体积$= \int_0^{2 \pi }\, d \phi \int_0^{ \pi } \sin \theta\, d \theta \int_0^R \rho^2\, d \rho = 2 \pi \int_0^{ \pi } \sin \theta \frac{R^3}{3 }\, d \theta = \frac{2}{3 } \pi R^3 [- \cos \theta]_0^{ \pi } = \frac{4}{3 } \pi R^3$。

• 四面体 (三棱锥或者说3维单纯形)：顶点在原点，三条长度为l的边沿着各个笛卡尔坐标系轴向的四面体的体积可以通过简化公式计算，因为xy平面和'z'轴互相垂直，x和y垂直，被积函数是常数1。

体积$= \int_0^\ell dx \int_0^{\ell-x }\, dy \int_0^{\ell-x-y }\, dz = \int_0^\ell dx \int_0^{\ell-x } (\ell - x - y)\, dy$

$= \int_0^\ell (\ell^2 - 2\ell x + x^2 - \frac{ (\ell-x)^2 }{2 })\, dx = \ell^3 - \ell \ell^2 + \frac{\ell^3}{3 } - \left[\frac{\ell^2}{2 } - \ell x + \frac{x^2}{2 }\right]_0^\ell =$

$= \frac{\ell^3}{3 } - \frac{\ell^3}{6 } = \frac{\ell^3}{6}$

验证：体积 = 底面积×高/3 = $\frac{\ell^2}{2 } \cdot \ell/3 = \frac{\ell^3}{6}$。

反常区间的例子。

多重广义积分

定义域无界或者函数值在靠近定义域边界时无界的情况下，可以引入二重广义积分或者三重广义积分。

多重积分和累次积分

富比尼定理断言若

$\int_{A\times B} |f(x,y)|\,d(x,y)<\infty,$

也即，积分绝对收敛，则多重积分和累次积分给出同样的结果，

$\int_{A\times B} f(x,y)\,d(x,y)=\int_A\left(\int_B f(x,y)\,dy\right)\,dx=\int_B\left(\int_A f(x,y)\,dx\right)\,dy$。

一个特例是如果$|f(x,y)|$是有界函数而A和B为有界集时。

如果积分不是绝对收敛，必须小心，不要混淆多重积分和累次积分的概念，特别是当它们采用形式上相同的记法的时候。记法

$\int_0^1\int_0^1 f(x,y)\,dy\,dx$

在某些情况下表示累次积分而非真正的双重积分。累次积分中，外围的积分

$\int_0^1 \cdots \, dx$

是对于如下x的函数关于x的积分

$g(x)=\int_0^1 f(x,y)\,dy$。

双重积分却是定义在xy平面的区域上。若双重积分存在，则它等于两个累次积分中的任何一个（或者"dy dx"或者"dx dy"），它也就是通过其中之一来计算的。但是有时这两个累次积分存在，而双重积分不存在。这种情况下，有时两个累次积分不相等，也即，

$\int_0^1\int_0^1 f(x,y)\,dy\,dx \neq \int_0^1\int_0^1 f(x,y)\,dx\,dy$。

这是条件收敛的积分的重排序的一个例子。

如果要强调使用双重积分而非累次积分时，可以采用如下记法

$\int_{[0,1]\times[0,1]} f(x,y)\,dx\,dy$

一些实际应用

这些积分在物理中有大量应用。

力学中，转动惯量可以作为密度乘以和转轴的距离的平方的体积分（三重积分）计算：

$I_z = \iiint_V \rho r^2\, dV$。

在电磁学中，麦克斯韦方程组可以写作多重积分，用以计算总磁场和电场。下例中，由电荷分布产生的电场通过向量函数的三重积分得到：

$\vec E = \frac {1}{4 \pi \epsilon_0} \iiint \frac {\vec r - \vec r'}{\left \| \vec r - \vec r' \right \|^3} \rho (\vec r')\, \operatorname{d}^3 r'$。

参看

• 和多重积分相关的实分析定理：
  • 散度定理
  • 斯托克斯定理
  • 格林定理

参考

• Robert A. Adams - Calculus: A Complete Course (5th Edition) ISBN 0-201-79131-5.

外部链接

• 埃里克·韦斯坦因, 多重积分 at MathWorld
• L.D. Kudryavtsev, Multiple integral//Hazewinkel, Michiel, 数学百科全书, 克鲁维尔学术出版社. 2001, ISBN 978-1556080104 
• Mathematical Assistant on Web 笛卡尔坐标系下和极坐标下的双重积分的在线计算 （包括求解过程中的中间步骤，由Maxima (软件)支持）